Google Optimization Tools介绍

Google Optimization Tools(OR-Tools)是一款专门快速而便携地解决组合优化问题的套件。它包含了：

• 约束编程求解器。
• 简单而统一的接口，用于多种线性规划和混合整数规划求解，包括 CBC、CLP、GLOP、GLPK、Gurobi、CPLEX和SCIP。
• 图算法 (最短路径、最小成本、最大流量、线性求和分配)。
• 经典旅行推销员问题和车辆路径问题的算法。
• 经典装箱和背包算法。

Google使用C++开发了OR-Tools库，但支持Python，C#，或Java语言调用。

安装Google OR-Tools

Google OR-Tools的源码在[Github] google/or-tools。其它开发环境下的安装如下。

Linux or Mac下安装

1. 确认使用了Python 2.7+，3.5+版本，以及pip 9.0.1+版本。

2. Mac OSX系统需要安装命令行工具Xcode，在Terminal中执行xcode-select --install。

Linux系统需要安装g++，在Terminal中执行sudo apt-get install g++ make。

如果使用C#请确认安装了Mono 4.2.0+的64位版本。

3. 在Terminal中执行pip install --upgrade ortools直接安装Python版本的OR-Tools包。C++/Java/C#版本的链接为：Mac, Ubuntu 17.04, Ubuntu 16.04, Ubuntu 14.04, CentOS 7, Debian 9 ，下载到指定目录后执行make all。

Windows下安装

Python版本的包的安装和Linux一样，可自行选用合适的开发工具。若是使用C++、C#，推荐使用64位版本的Windows10操作系统，并且使用Microsoft Visual Studio 2015 或者 2017作为开发工具，相应的库文件下载地址为： Visual Studio 2017 the Visual Studio 2015。

• C++使用lib/ortools.lib, 并且将or‑tools/include添加到项目引用。
• Java使用jar命令调用lib/com.google.ortools.lib的方式，并且将 ‑Djava.library.path=PATH_TO_or‑tools/lib添加到命令行。
• C#添加bin/Google.OrTools.dll到项目依赖，或者使用NuGet搜索Google.OrTools进行安装。

Demo

以下是几种支持语言的demo，运行一下验证是否安装正确。

C++ 代码

#include "ortools/linear_solver/linear_solver.h"
#include "ortools/linear_solver/linear_solver.pb.h"

namespace operations_research {
  void RunTest(
    MPSolver::OptimizationProblemType optimization_problem_type) {
    MPSolver solver("Glop", optimization_problem_type);
    MPVariable* const x = solver.MakeNumVar(0.0, , "x");
    MPVariable* const y = solver.MakeNumVar(0.0, , "y");
    MPObjective* const objective = solver.MutableObjective();
    objective->SetCoefficient(x, );
    objective->SetCoefficient(y, );
    objective->SetMaximization();
    solver.Solve();
    printf("\nSolution:");
    printf("\nx = %.1f", x->solution_value());
    printf("\ny = %.1f", y->solution_value());
  }

  void RunExample() {
    RunTest(MPSolver::GLOP_LINEAR_PROGRAMMING);
  }
}

int main(int argc, char** argv) {
  operations_research::RunExample();
  return ;
}

C# 代码

using System;
using Google.OrTools.LinearSolver;

public class my_program
{
  private static void RunLinearProgrammingExample(String solverType)
  {
    Solver solver = Solver.CreateSolver("IntegerProgramming", solverType);
    Variable x = solver.MakeNumVar(0.0, 1.0, "x");
    Variable y = solver.MakeNumVar(0.0, 2.0, "y");
    Objective objective = solver.Objective();
    objective.SetCoefficient(x, );
    objective.SetCoefficient(y, );
    objective.SetMaximization();
    solver.Solve();
    Console.WriteLine("Solution:");
    Console.WriteLine("x = " + x.SolutionValue());
    Console.WriteLine("y = " + y.SolutionValue());
  }

  static void Main()
  {
    RunLinearProgrammingExample("GLOP_LINEAR_PROGRAMMING");
  }
}

Python 代码

from __future__ import print_function
from ortools.linear_solver import pywraplp

def main():
  solver = pywraplp.Solver('SolveSimpleSystem',
                           pywraplp.Solver.GLOP_LINEAR_PROGRAMMING)
  x = solver.NumVar(0, 1, 'x')
  y = solver.NumVar(0, 2, 'y')
  objective = solver.Objective()
  objective.SetCoefficient(x, 1)
  objective.SetCoefficient(y, 1)
  objective.SetMaximization()
  solver.Solve()
  print('Solution:')
  print('x = ', x.solution_value())
  print('y = ', y.solution_value())

if __name__ == '__main__':
  main()

Java 代码

import com.google.ortools.linearsolver.MPConstraint;
import com.google.ortools.linearsolver.MPObjective;
import com.google.ortools.linearsolver.MPSolver;
import com.google.ortools.linearsolver.MPVariable;

public class my_program {
  static { System.loadLibrary("jniortools"); }

  private static MPSolver createSolver (String solverType) {
    return new MPSolver("my_program",
                        MPSolver.OptimizationProblemType.valueOf(solverType));
  }

  private static void runmy_program(String solverType,
                                                  boolean printModel) {
    MPSolver solver = createSolver(solverType);
    MPVariable x = solver.makeNumVar(0.0, 1.0, "x");
    MPVariable y = solver.makeNumVar(0.0, 2.0, "y");
    MPObjective objective = solver.objective();
    objective.setCoefficient(y, 1);
    objective.setMaximization();
    solver.solve();
    System.out.println("Solution:");
    System.out.println("x = " + x.solutionValue());
    System.out.println("y = " + y.solutionValue());
  }

  public static void main(String[] args) throws Exception {
    runmy_program("GLOP_LINEAR_PROGRAMMING", false);
  }
}

执行结果如图：

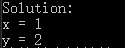
下一篇这个系列的文章，将具体介绍一种约束求解的应用场景。