【noip模拟赛3】贾老二的工件 （模拟）

描述

贾老二有很多工件，最常见的工件都是长条形的，但其顶端是凹凸不平的，即不同位置的高度不同。现在贾老二有两个最常见的工件，他想将它们完全放入另一种罕见的可容纳高度不超过k的工件中，问该罕见的工件的最小长度。

输入

输入来自文件jia.in，包括三行。第一行包含一个不超过20的正整数k；接下来每行有一个长度不超过100的正整数串，其中的每个数都在1到9之间，表示该常见工件对应位置的高度。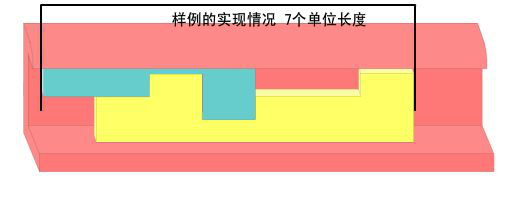

输出

包括一个数字即罕见的工件的最小长度。如果无解则输出“Impossible”。

输入样例 1

4
2213
231223

输出样例 1

7

输入样例 2

1
2112
122111

输出样例 2

Impossible

非常麻烦的模拟  注意：零件可以翻转！！！
把a，b变成
 2213                 --->         22130000000
 231223               --->         00002312230000

然后在a的左端加0 就右移了
第一次扫到不是0设置左坐标
扫到为0设置右坐标  （所以a的最右边要多出一个0）

string的各种操作真的非常方便！！！

#include<bits/stdc++.h>
using namespace std;
//input
#define RI(n) scanf("%d",&(n))
#define RII(n,m) scanf("%d%d",&n,&m);
#define RIII(n,m,k) scanf("%d%d%d",&n,&m,&k)
#define RS(s) scanf("%s",s)
#define LL long long
#define REP(i,N)  for(int i=0;i<(N);i++)
#define CLR(A,v)  memset(A,v,sizeof A)
//////////////////////////////////
#define N 2050
#define inf -0x3f3f3f3f

int main()
{
    int d;
    RI(d);
    string a,b;

    cin>>a>>b;
    string temp=a;
    int lena=a.size();
    int lenb=b.size();
    REP(i,lenb+) a+="";//给right留空位
    REP(i,lena) b=""+b+"";

    int ans=INT_MAX;

    REP(i,lenb+lena)
    {
        int j=;
        int left=inf,right=;
        int flag=;
        while(a[j]&&b[j])
        {
            int k=a[j]-''+b[j]-'';
            if(k&&left==inf){left=j;right=inf;}//取左
            if(!k&&right==inf){right=j;}//取右
            if(k>d){flag=;break;}
            j++;
        }
        if(flag)ans=min(ans,right-left);
        a=""+a;
    }

    a="";
    for(int i=;i<temp.size();i++)
        a=temp[i]+a;
    REP(i,lenb+) a+="";

     REP(i,lenb+lena)
    {
        int j=;int left=inf,right=;
        int flag=;
        while(a[j]&&b[j])//当由乙方不存在时结束
        {
            int k=a[j]-''+b[j]-'';
            if(k&&left==inf){left=j;right=inf;}
            if(!k&&right==inf){right=j;}
            if(k>d){flag=;break;}
            j++;
        }
        if(flag)ans=min(ans,right-left);
        a=""+a;
    }

    if(ans==INT_MAX)printf("Impossible");
    else cout<<ans;
}