对NP问题的一点感想

一.概述

回忆欧拉回路问题，要求找出一条经过图的每条边恰好一次的路径，这个问题是线性可解的。哈密尔顿圈问题是找一个简单圈，该圈包括图的每一个顶点。对于这个问题，现在还没有发现线性算法。

对于有向图的单源无权最短路径问题也是有线性时间可解的，但是对应的最长简单路径问题（longest-simple-path）尚没有发现线性算法。

这些问题的变化，其情况实际上比描述得还要糟。对于这些变种问题不仅不知道线性算法，而且不存在保证以多项式时间运行的已知算法。这些问题的一些熟知算法对于某些情况可能要花费指数时间。

由于相当复杂，我在下面的讨论也只是非正式的，所以可能会存在一些讨论不到位的遗憾。

其实存在大量的重要的问题，它们在复杂性上大体是等价的。这些问题形成了一个类，称为NP-完全（NP-complete）问题。这些NP-完全问题精确的复杂度仍然需要确定并且在计算机理论科学方面仍然是最重要的开放性问题。或者这些问题都有多项式时间算法，或者都没有多项式时间算法。

二.难与易

给问题分类时，第一步要考虑分界。我们看到许多问题都可以用线性时间求解。我们还看到某些O（logN）的运行时间，但是它们或者假定已经做了某些预处理（如输入数据已读入或者数据结构已经建立），或者出现在运算实例中。例如，gcd（最大公因数）算法，当用于两个数M和N时，花费O（logN）的时间。由于这两个数分别由logM和logN个二进制位组成，因此gcd算法实际上花费的时间对于输入数据的量而言是线性的。由此可知，当我们度量运行时间时，我们将把运行时间考虑成输入数据的量的函数。一般来说，不能期望运行时间比线性时间更好。

另一方面，的确存在某些真正困难的问题（以至于它们不可能被解出）。但这并不意味着我们懊恼叹息等着天才来解决。正如实数不足以表示X²<0 的解那样，可以证明的是，计算机不可能解决碰巧发生的每一个问题。这些“不可能”问题，叫做不可判定问题（undecidable problem）。

一个特殊的不可判定问题就是停机问题（halting problem）。是否能够使Java编译器拥有一个附加的特性，即不仅能够检查语法错误，而且能够检查所有的无限循环？这似乎是一个比较难的问题，但是我们或许期望，假如某些聪明的程序员花上足够的时间，或许可能编制出这种增强编译器。

这个问题是不可判定的，其直观原因在于，这样的一个程序可能很难检查它自己。由于这个原因，有时候这些问题被叫做递归不可判定的（recursively undecidable）。

假如一个无限循环检查程序能够写出，那么它肯定可以用于自检。假设此时我们可以编写这样的一个程序，叫做LOOP。LOOP把一个程序P作为输入并使P自身运行。如果P自身运行时出现循环，则显示短语YES。如果P自身运行终止了，那么自然显示NO。现在，我们换个角度，让LOOP进入无限循环。

当LOOP将自身作为输入会发生什么呢？或者LOOP停止，或者不停止。问题在于，这里面存在罗素悖论。

根据我们的定义，如果P(P)终止，则LOOP(P)进入一个无限循环。设当P=LOOP时，P(P)终止。此时，按照LOOP程序，LOOP(P)应该进入一个无限循环。因此，我们必须让LOOP(LOOP)终止并进入一个无限循环，显然这是不可能的。另一方面，设当P=LOOP时，P(P)进入一个无限循环，则LOOP(P)必然终止，我们得到了同样的一组矛盾。因此可以说，LOOP程序不存在。

三.NP类

NP类是在难度上逊于不可判定问题的类。NP代表非确定性多项式时间（nondeterministic polynomial-time）。确定性机器在每一时刻都在执行一条指令。根据这条指令，机器在去执行某条接下来的指令，这是唯一确定的。而一台非确定性机器对其后的步骤是有选择的。它可以自由进行它想要的任意的选择，如果这些后面的步骤中有一条是导致问题的解，那么它将总是选择这个正确的步骤。因此，非确定性机器有很好的猜测与优化能力。这好像一个很奇怪的模型，因为没有人能够建立这样一台机器，还因为这台机器是对标准计算机的令人难以置信的改进（这时候所有的问题都变成易解的了）。非确定性是非常有用的理论结构。此外，非确定性也不像人们想象的那样强大。比如，即使使用非确定性，不可判定问题仍然是不可判定的。

检验一个问题是否属于NP的简单方法就是将该问题用“是/否（yes/no）问题”的语言描述。如果我们在多项式时间内能够证明一个问题的任意“是”的实例是正确的，那么该问题就是NP类。我们不必担心“否”的实例，因为程序总是进行正确的选择。因此，对于哈密顿圈问题，一个“是”的实例就是图中任意一个包含所有顶点的简单的回路。由于给定一条路径，验证它是否真的是哈密尔顿圈是一件简单的事情，因此哈密尔顿圈问题属于NP。诸如“存在长度大于K的简单路径吗？”这样的问题也可能容易验证从而属于NP。满足这条性质的任何路径均可容易检验。

由于解本身显然提供了验证方法，因此，NP类包括所有具有多项式时间解的问题。人们会想到，既然验证一个问题要比经过计算提出一个答案简单得多，因此在NP中就会存在不具有多项式时间解法的问题。这样的问题至今没有发现，于是，完全有可能非确定性并不是如此重要的改进。

也并不是所有可判定性问题都属于NP。考虑确定一个图是否没有哈密尔顿圈的问题。证明一个图有哈密尔顿圈是相对简单的事情——我们只需要找到一个就可以了。然而却没有人知道如何以多项式时间证明一个图没有哈密尔顿圈。似乎只剩下一个方法，就是枚举并验证。因此，无哈密尔顿圈的问题不知道属不属于NP。

四.NP-完全问题

在已知属于NP的所有问题中，存在一个子集，叫做NP-完全问题，包含了NP中最难的问题。NP-完全问题有一个性质：NP中的任一问题都能够以多项式时间归约成NP-完全问题。

问题 P₁可以归约成问题P₂ 如下：设有一个映射，使得 P₁的任何实例都可以变换成P₂ 的一个实例。求解 P₂，然后将答案映射回原始的解答。作为一个例子，考虑把数以十进制输入到一只计算器。将这些十进制数转换成二进制数，所有的计算都以二进制进行。然后，再把最后的答案转变成十进制显示。对于可多项式地归约成P₂ 的 P₁，与变换相联系的所有工作必须以多项式时间完成。

NP-完全问题是最难的NP问题的原因在于，一个NP-完全问题基本上可以用作NP中任何问题的子例，其花费的只不过是多项式的开销量。因此，如果任意NP-完全问题有一个多项式时间解，那么NP中的每一个问题必然都有一个多项式时间解。

假设我们有一个NP-完全问题 P₁，并设P₂ 已知属于NP。再进一步假设 P₁多项式地归约成 P₂，使得我们可以通过 P₂求解 P₁只多耗费了多项式时间。由于 P₁是NP-完全的，NP中的每一个问题都可以归约成 P₁。对于多项式的封闭性，我们看到，NP中的每一个问题均可多项式地归约成P₂ 。因此， P₂是NP-完全的。

五.巡回售货员问题

给定一个完全图G=（V,E），它的边值以及整数K，是否存在一个访问所有顶点并且总值小于等于K的简单回路？

巡回售货员问题是NP-完全的。容易看到，它的解可以用多项式时间检验，当然它属于NP。为了证明它是NP-完全的，我们可以多项式地将哈密尔顿圈问题归约为巡回售货员问题。为此，构造出一个新图G’ , G’ 和G有相同的顶点。对于G‘ 的每一条边（v , w），如果（v , w）∈ G ,那么它就有权1，否则，它的权就是2.我们选取K=|V|。

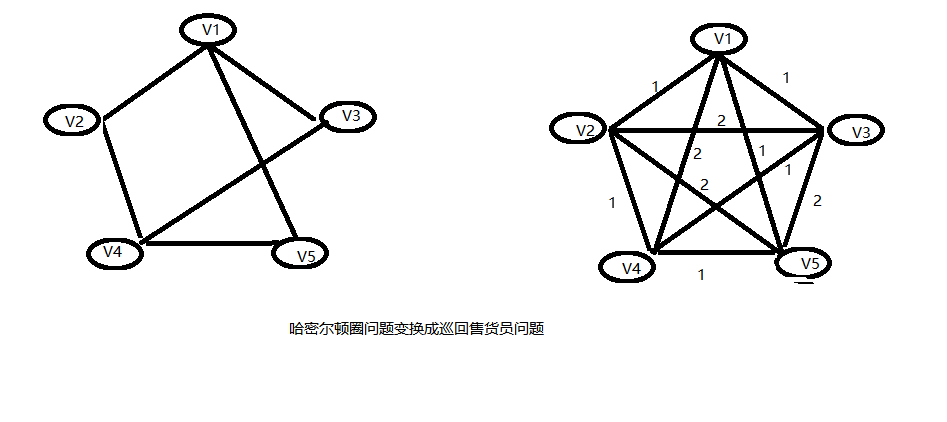
容易验证，G有一个哈密尔顿圈当且仅当G‘ 有一个总权为|V|的巡回售货员的巡回路线。

现在有许多问题已知是NP-完全问题。为了证明某个新问题是NP-完全问题，必须证明它属于NP，然后构造一个适当的NP-完全问题变换到该问题。

那么第一个NP-完全问题是怎么具体地被证明的呢？由于证明一个问题是NP-完全需要从另一个NP-完全问题变换到它，因此必然存在某个NP-完全问题，对于这个问题不能用上面的思路。第一个被证明的NP-完全问题是可满足性（satisfiability）问题。这个问题把一个布尔表达式作为输入并提问该表达式对各变量的一次赋值取值true。

可满足性问题当然属于NP，因为容易计算一个布尔表达式的值并检查结果是否为真（true）。在1971年，Cook通过直接证明NP中所有问题都可以变换成可满足性问题而证明了NP-完全问题。为此，他用到了对NP中每一个问题都已知的事实：NP中的每一个问题都可以用一台非确定性计算机在多项式时间内求解。计算机的这种形式化模型就是图灵机（Turing machine）。Cook指出这台机器的动作如何能够用一个极其复杂但仍是多项式的冗长的布尔公式来模拟。该布尔公式为真，当且仅当在由图灵机运行的程序对其输入得到一个“是”的答案。

一旦可满足性问题被证明NP-完全，则一大批新的NP-完全问题，包括某些经典的问题，也被证明是NP-完全的。

其实还有还多更加著名的NP-完全问题，比如装箱问题、背包问题、着色问题、团问题。这些NP-完全问题相当广泛，包括来自操作系统、数据库、运筹学、逻辑学等，特别是图论等领域。