[Fundamental of Power Electronics]-PART I-2.稳态变换器原理分析-2.1 引言

2.1 引言

在上一章中，介绍了降压变换器作为降低直流电压的一种方法，其仅使用非耗散开关，电感器和电容器。开关状态变换产生一个矩形波形\(v_{s}(t)\)，如图2.1所示。当开关位于位置1时，该电压\(v_{s}(t)\)等于直流输入电压\(V_{g}\)；当开关位于位置2时，该电压\(v_{s}(t)\)等于零。实际上，开关是使用功率半导体器件（例如晶体管和二极管）实现的，可根据需要控制功率开关器件导通和关断以执行理想开关的功能。开关频率\(f_{s}\)取决于半导体器件的开关速度，等于开关周期\(T_{s}\)的倒数,一般的开关频率通常在1 kHz至1MHz的范围内。占空比D是开关在位置1上所占时间比例(一个周期内)，并且其是介于0和1之间的数字。占空比的补码(翻译不准确) \(D^{'}\)定义为(1-D)。

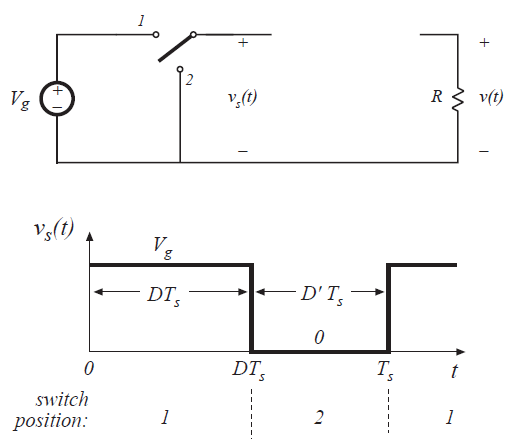
Fig 2.1 SPDT switch changes dc component，Switch output voltage waveform

开关变换降低了电压的直流分量：开关输出电压的直流分量小于变换器的直流输入电压\(V_{g}\),根据傅里叶变换，我们知道\(v_{s}(t)\)的直流分量由其平均值\(<v_{s}>\)或者下式给出：

\[<v_{s}>=\frac{1}{T_{s}}{\int_1^{T_{s}}v_{s}(t)dt} \tag{2-1}
\]

如图2.2所示，积分由曲线下的面积给出，\(D{T_{s}}{V_{g}}\)或者平均值为:

\[<v_{s}>=\frac{1}{T_{s}}({D{T_{s}}{V_{g}})}=D{V_{g}} \tag{2-2}
\]

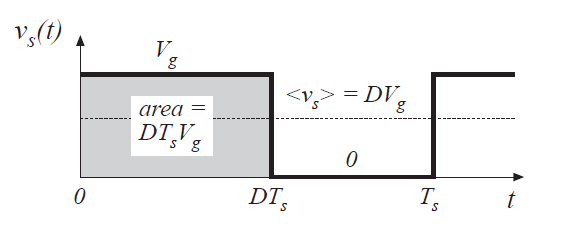
Fig 2.2 Dc component of switch output voltage

因此，\(v_{s}(t)\)的平均值或直流分量等于占空比乘以直流输入电压\(V_{g}\)。开关变换将直流电压降低至其D倍。

剩下要做的就是插入一个低通滤波器，如图2.3所示。这个滤波器设计为能够通过\(v_{s}(t)\)的直流分量，而阻断\(v_{s}(t)\)的开关频率次等一系列谐波成分。那么输出电压\(v_{t}\)就等于\(v_{s}(t)\)的直流分量。

\[v\approx<v_{s}>=D{V_{g}} \tag{2-3}
\]

图2.3的变换器已使用无耗散元件实现(电感，电容和开关)。就其理想程度而言，电感器，电容器和开关不会消耗功率。例如，当开关闭合时，其电压降为零，而当开关断开时，电流为零。在任何一种情况下，开关消耗的功率均为零。因此，可以获得接近100％的效率。因此，当认为各元件为理想情况下，我们可以使用无损电网络实现更改直流电压的目标。

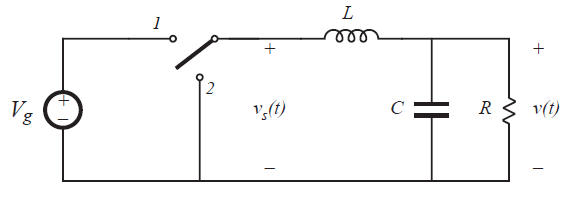
Fig 2.3 Insertion of low-pass filter to remove switching harmonics and pass only dc component

如图2.3所示的电路还允许对输出进行控制。图2.4是这个变换器的控制特性，绘出了式(2.3)给出的输出电压与占空比之间的关系。buck变换器具有一个线性的特性，同时由于\(0\leq{D}\leq1\),输出电压小于或等于输入电压。通常通过控制占空比D构建反馈控制系统来控制输出电压。同样还可以通过占空比随时间变化且电压跟随来构建逆变器或者功率放大器。

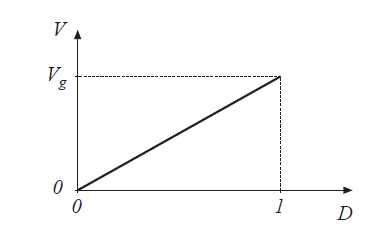
Fig 2.4 Buck converter output voltage vs duty cycle

Buck变换器只是许多可能的开关转换器之一。图2.5给出了另外两个常用的执行不同电压转换功能的变换器。在升压变换器中，电感和开关的位置相反。本章稍后将介绍升高电压的升压变换器。另一个转换器，降压-升压转换器，可以提升或降低电压的幅值，但极性却相反。因此，在正输入电压下，理想的降压-升压转换器可以产生任何幅度的负输出电压。首先，这可能令人惊讶，可以产生幅度大于输入幅度或极性相反的直流输出电压。但是确实有可能使用仅由电感，电容和嵌入式开关组成的无源电网络来产生任何所需的直流输出电压。

Fig 2.5 Three basic dc-dc converters

在上述讨论中，我们可以基于傅里叶变换利用几个简单的参数如式(2.3)所示的buck变换器的输出电压表达式。但我们可能还不能立即很容易的利用这些参数推导出如boost，buck-boost，或者其他变换器的输出电压表达式。本章的目标就是建立一种更加通用的方法来分析由电感、电容以及开关器件组成的任何形式的变换器。[1-8]

推导了电感伏秒平衡和电容电荷平衡的原理。这些可用于求解开关变换器的电感电流和电容电压。小纹波或线性纹波(暂且这么叫，还没想好怎么翻译)近似是一种有用的近似方法，极大地方便了分析。还讨论了一些用于确定滤波器参数的简单方法。

[参考文献]