dsu on tree (树上启发式合并) 详解

一直都没出过算法详解，昨天心血来潮想写一篇，于是 dsu on tree 它来了

1、前置技能

1.链式前向星（vector 建图）

2.dfs 建树

3.剖分轻重链，轻重儿子

重儿子	一个结点的所有儿子中拥有最多子树的儿子
轻儿子	一个结点的所有儿子中不是重儿子的儿子
重边	父亲与重儿子的连边
轻边	父亲与轻儿子的连边
重链	一堆重边连接而成的链
轻链	一堆轻边连接而成的链

2、什么是 dsu on tree（树上启发式合并） ？

dsu on tree 其实就是个优雅的暴力算法，和它一起共被称为优雅暴力的算法还有莫队

所谓优雅的暴力大概是指：“优雅思想，暴力的操作”

例如莫队我们知道它是将整个区间分块，再将询问的区间排序，最后暴力的维护所有询问的区间

其中 "整个区间分块，询问的区间排序" 为优雅的思想，而 "暴力的维护所有询问的区间" 为暴力的操作

因为需要将询问的区间排序，我们就需要先将询问的区间保存下来，也就是要离线

dsu on tree 和莫队类似，也需要离线（它们同属于静态算法）

dsu on tree 优雅的思想：

对于以 u 为根的子树

①. 先统计它轻子树(轻儿子为根的子树)的答案，统计完后删除信息

②. 再统计它重子树(重儿子为根的子树)的答案 ，统计完后保留信息

③. 然后再将重子树的信息合并到 u上

④. 再去遍历 u 的轻子树，然后把轻子树的信息合并到 u 上

⑤. 判断 u 的信息是否需要传递给它的父节点（u 是否是它父节点的重儿子）

dsu on tree 暴力的操作

dsu on tree 暴力的操作体现于统计答案上（不同的题目统计方式不一样）

3、dsu on tree 的过程演示及代码

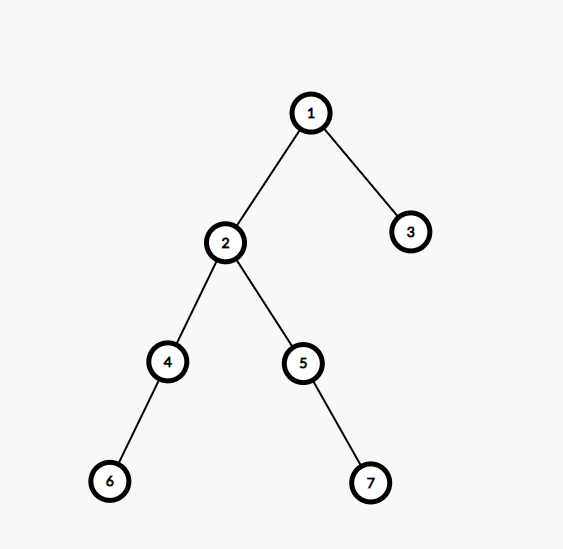
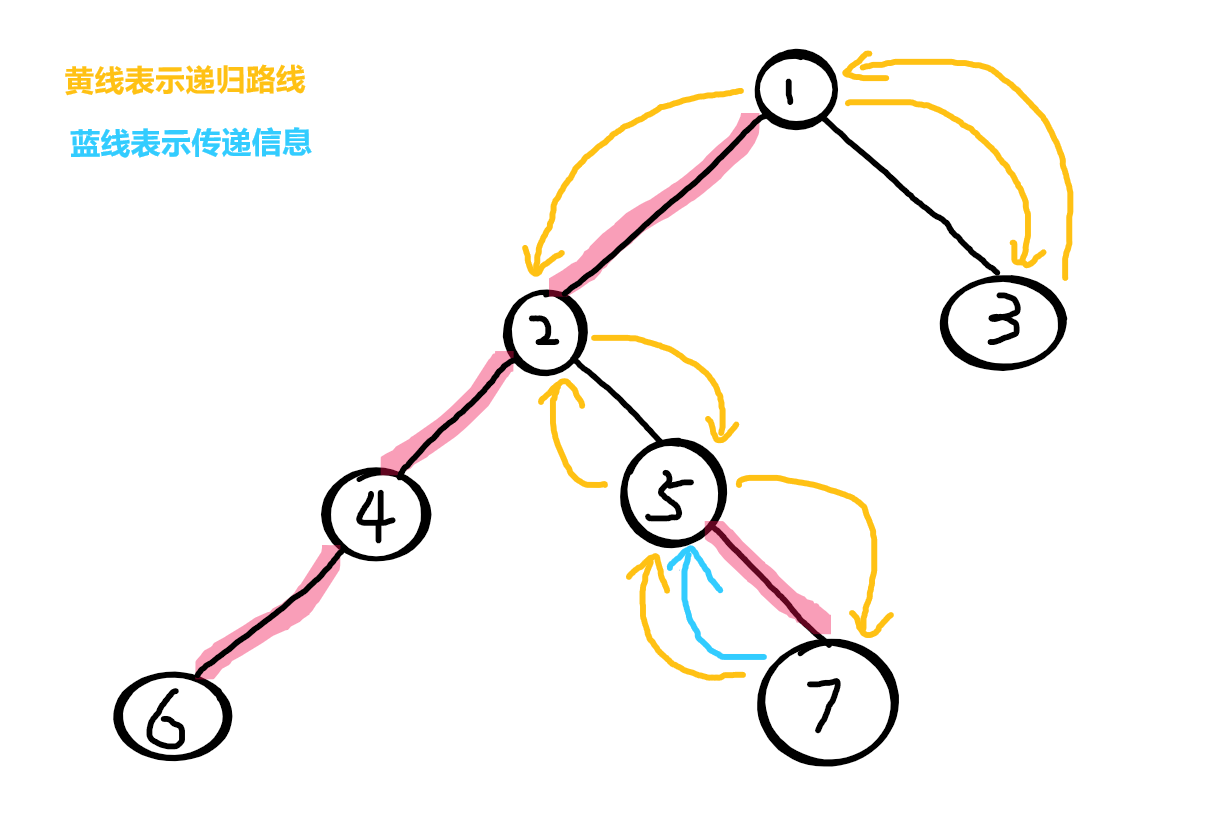
1.图示

• 1 的重儿子为 2，轻儿子为 3

• 2 的重儿子为 4，轻儿子为 5

• 3 没有重儿子，没有轻儿子

• 4 的重儿子为 6，没有轻儿子

• 5 的重儿子为 7，没有轻儿子

• 6 没有重儿子，没有轻儿子

• 7 没有重儿子，没有轻儿子

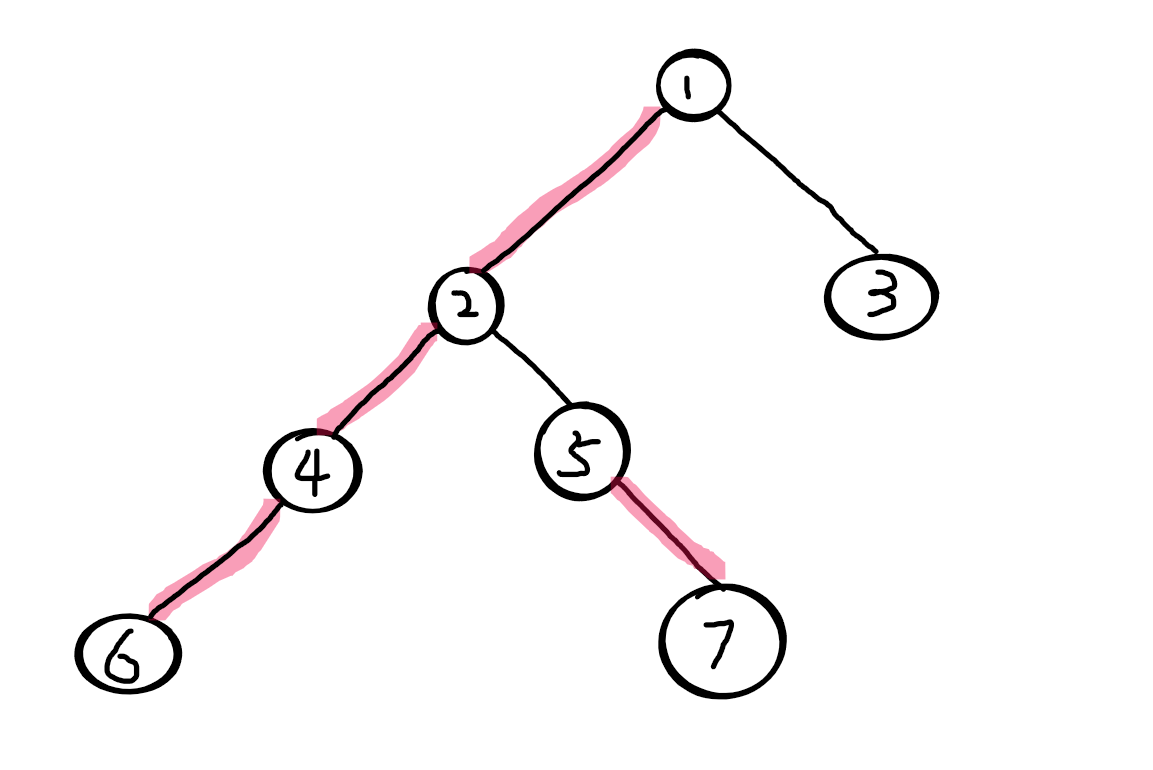
为了更好观看，我们将节点与其重儿子的连线描红

我们从根节点1进入，先找1的轻儿子，发现3，进入3

3没有别的儿子可以进入了，于是统计3的信息

统计完后即将返回父节点 1

因为1-3的边没有被描红边、3不是1的重儿子（不传递3的信息），所以删除3的信息再返回 1

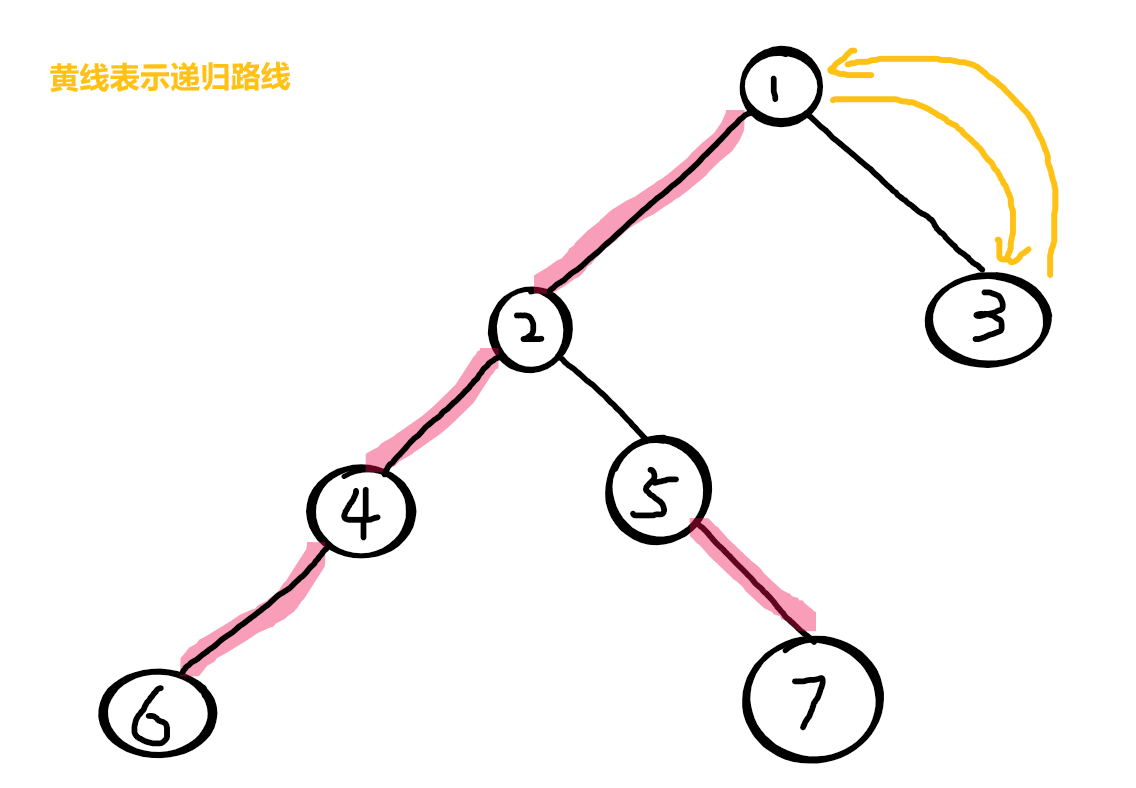
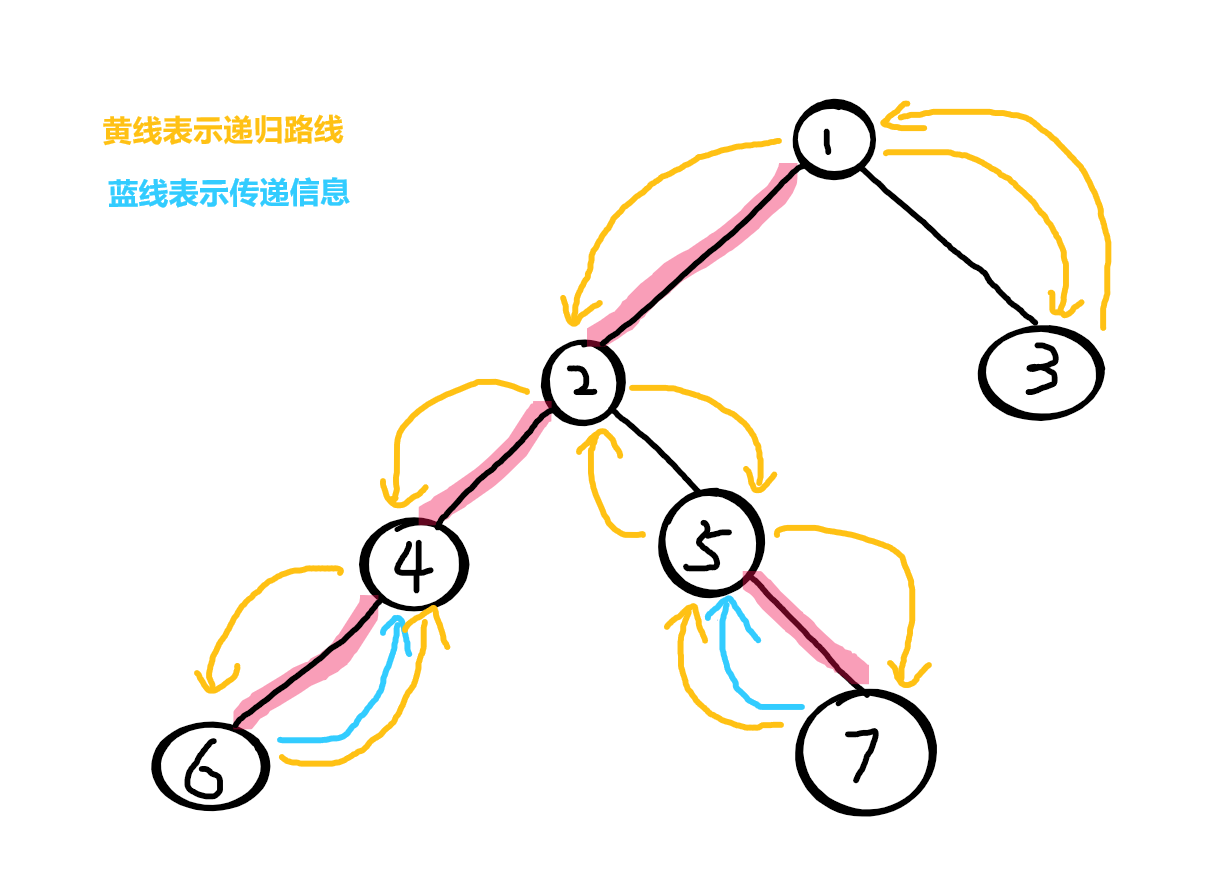
发现1没有别的轻儿子了，就找重儿子，发现2，进入2

进入2后，再找2的轻儿子，发现5，进入5

发现5没有轻儿子了，就找重儿子，发现7，进入 7

7 没有别的儿子可以进入了，于是统计 7 的信息

统计完后即将返回父节点 5

因为边5-7 有被描红边、7是5的重儿子，所以保留7的信息直接返回 5（传递7的信息的给5）

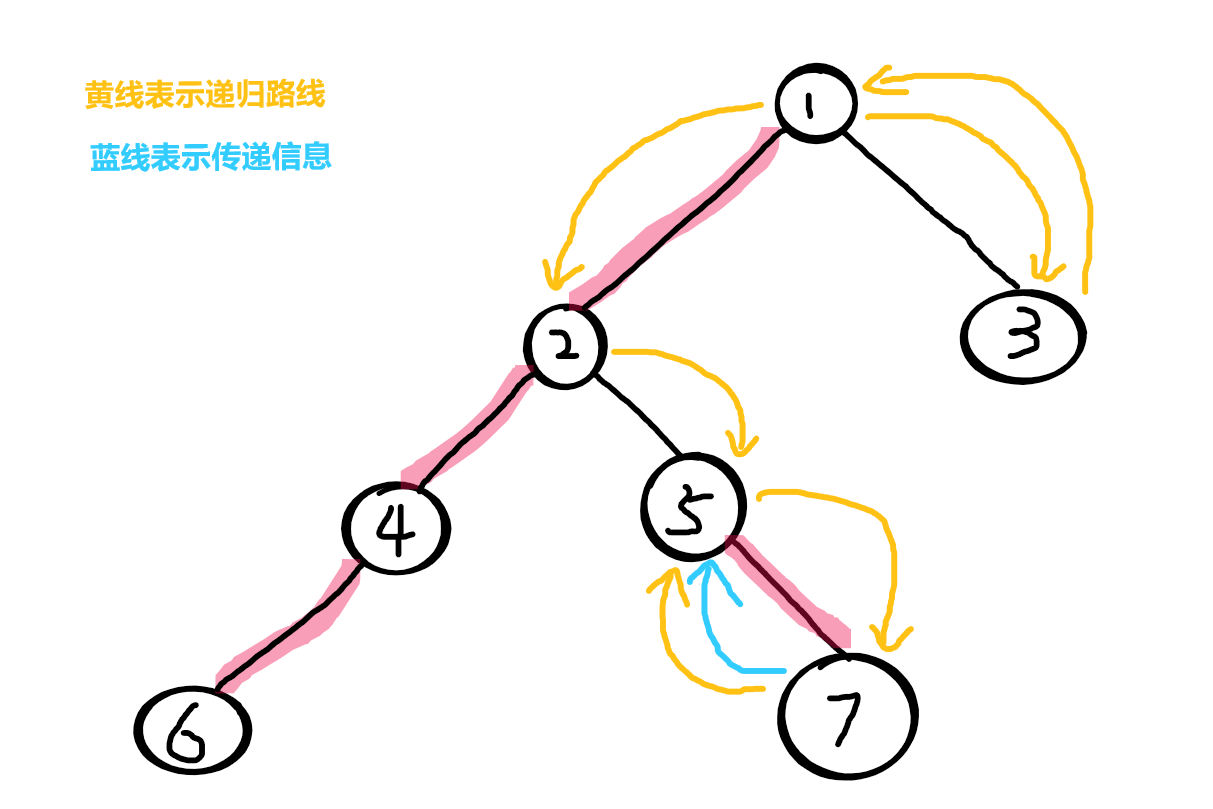
5 所有儿子都进入过了，于是统计 5 的信息

统计完后即将范围父节点 2

因为边2-5 没有被描红边、5不是2的重儿子，所以删除5的信息再返回 2

发现2没有其它轻儿子了，就找重儿子，发现4，进入4

发现4没有其它轻儿子了，就找重儿子，发现6，进入6

6 没有别的儿子可以进入了，于是统计 6 的信息

统计完后即将返回父节点 4

因为边4-6 有被描红边，6是4的重儿子，所以保留6的信息直接返回 4（传递6的信息的给4）

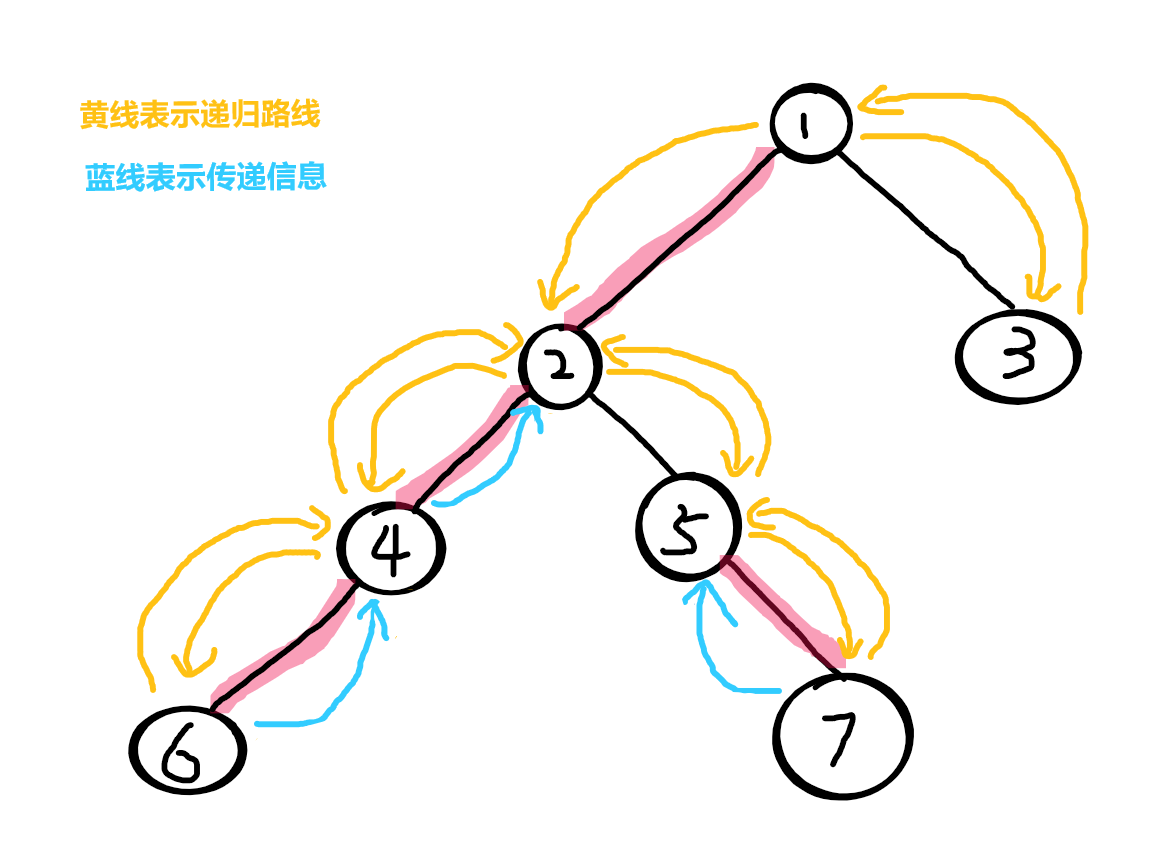
4 所有儿子都进入过了，于是统计 4 的信息

统计完后即将返回父节点 2

因为边2-4 有被描红边，4是2的重儿子，所以保留4的信息直接返回2（传递4的信息的给2）

2 所有儿子都进入过了，于是统计 2 的信息

2 接受了4传递的信息，但是并没有接受5传递给它的信息（被删除了）

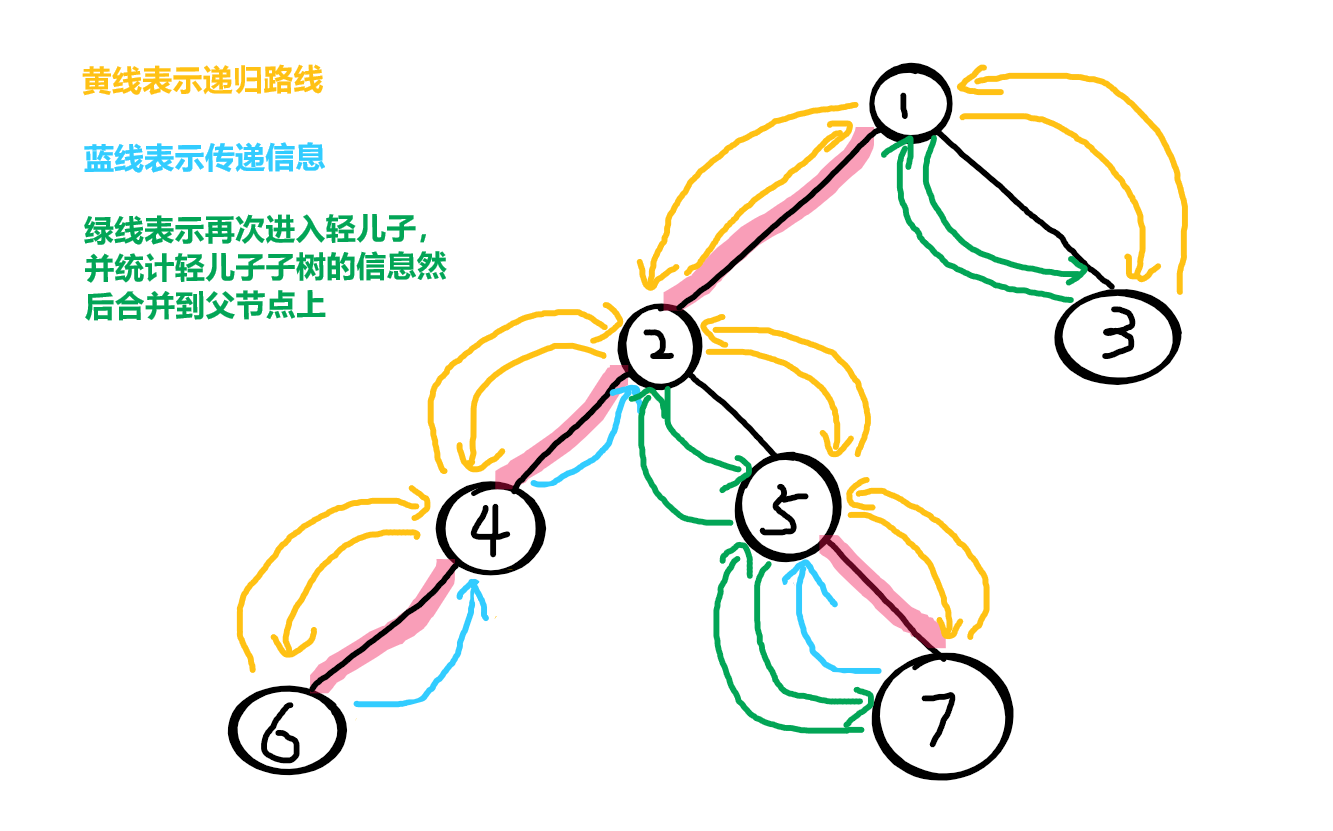
于是 2 再进入5（轻儿子），统计一遍以 5 为根的子树的信息，再将该信息合并到 2上

统计完后 2 后即将返回父节点 1

因为边1-2 有被描红边，2是1的重儿子，所以保留2的信息直接返回1（传递2的信息的给1）

1 所有儿子都进入过了，于是统计 1 的信息

1 接受了2传递的信息，但是并没有接受3传递给它的信息（被删除了）

于是 1 再进入3（轻儿子），统计一遍以 3 为根的子树的信息，再将该信息合并到 1 上

至此，整个 dsu on tree 的过程结束

2.代码

struct Edge{
	int nex , to;
}edge[N << 1];
int head[N] , TOT;
void add_edge(int u , int v) // 链式前向星建图
{
	edge[++ TOT].nex = head[u] ;
	edge[TOT].to = v;
	head[u] = TOT;
}
int sz[N];   // sz[u] 表示以 u 为根的子树大小
int hson[N]; // hson[u] 表示 u 的重儿子
int HH;      // HH 表示当前根节点的重儿子
void dfs(int u , int far)
{
	sz[u] = 1;
	for(int i = head[u] ; i ; i = edge[i].nex) // 链式前向星
	{
		int v = edge[i].to;
		if(v == far) continue ;
		dfs(v , u);
		sz[u] += sz[v];
		if(sz[v] > sz[hson[u]]) hson[u] = v; // 选择 u 的重儿子
	}
}
void calc(int u , int far , int val) // 统计答案
{
	if(val == 1) ...; // val = 1，则添加信息
	else ...;         // val = -1，则删除信息
	......
    for(int i = head[u] ; i ; i = edge[i].nex)
    {
        int v = edge[i].to;
        if(v == far || v == HH) continue ; // 如果 v 是当前根节点的重儿子，则跳过
        calc(v , u , val);
    }
}
void dsu(int u , int far , int op)  // op 等于0表示不保留信息，等于1表示保留信息
{
	for(int i = head[u] ; i ; i = edge[i].nex)
	{
		int v = edge[i].to;
		if(v == far || v == hson[u]) continue ; // 如果 v 是重儿子或者父亲节点就跳过
		dsu(v , u , 0);     // 先遍历轻儿子 ，op = 0 :轻儿子的答案不做保留
	}
	if(hson[u]) dsu(hson[u] , u , 1) , HH = hson[u];
	// 轻儿子都遍历完了，如果存在重儿子，遍历重儿子（事实上除了叶子节点每个点都必然有重儿子）
	// op = 1 ， 保留重儿子的信息
	// 当前是以 u 为根节点的子树，所以根节点的重儿子 HH = hson[u]
	calc(u , far , 1); // 再次遍历轻儿子统计答案
        HH = 0;			   // 遍历结束 ，即将返回父节点，所以取消标记 HH
	if(!op) calc(u , far , -1); // 如果 op = -1，则 u 对于它的父亲来说是轻儿子，不需要将信息传递给它的父亲
}

4.经典例题讲解

题目编号	题目链接	题解链接
CF600E	https://codeforces.com/problemset/problem/600/E	https://www.cnblogs.com/StarRoadTang/p/14028212.html
CF570D	https://codeforces.com/problemset/problem/570/D	https://www.cnblogs.com/StarRoadTang/p/14028239.html
CF208E	https://codeforces.com/problemset/problem/208/E	https://www.cnblogs.com/StarRoadTang/p/14028265.html
CF246E	https://codeforces.com/problemset/problem/246/E	https://www.cnblogs.com/StarRoadTang/p/14028271.html
CF1009F	https://codeforces.com/problemset/problem/1009/F	https://www.cnblogs.com/StarRoadTang/p/14028284.html
CF375D	https://codeforces.com/problemset/problem/375/D	https://www.cnblogs.com/StarRoadTang/p/14028290.html
wannafly Day2 E	https://ac.nowcoder.com/acm/contest/4010/E?&headNav=acm	https://www.cnblogs.com/StarRoadTang/p/14028296.html
ccpc2020长春站F题	https://codeforces.com/gym/102832/problem/F	https://www.cnblogs.com/StarRoadTang/p/14028298.html
洛谷P4149	https://www.luogu.com.cn/problem/P4149	https://www.cnblogs.com/StarRoadTang/p/14028300.html

5.难题进阶

这是道较难的题，听说这也是 dsu on tree 的发明人专门为这个算法出的题

题目编号	题目链接	题解链接
CF741D	https://codeforces.com/contest/741/problem/D	https://www.cnblogs.com/StarRoadTang/p/14028301.html

    ┏┛ ┻━━━━━┛ ┻┓
    ┃　　　　　　┃
    ┃　　　━　　　      ┃
    ┃　┳┛　  ┗┳　    ┃
    ┃　　　　　　       ┃
    ┃　　　┻　　　    ┃
    ┃　　　　　　      ┃
    ┗━┓　　　┏━━━┛
      ┃　　　┃   神兽保佑
      ┃　　　┃   代码无BUG！
      ┃　　　┗━━━━━━━━━┓
      ┃　　　　　　　    ┣┓
      ┃　　　　         ┏┛
      ┗━┓ ┓ ┏━━━┳ ┓ ┏━┛
          ┃ ┫ ┫   ┃ ┫ ┫
          ┗━┻━┛   ┗━┻━┛