POJ 2352 树状数组

学习自：链接以及百度百科

以及：https://www.bilibili.com/video/av18735440?from=search&seid=363548948825132979

理解树状数组

概念

假设数组a[1..n]，那么查询a[1]+...+a[n]的时间是log级别的，而且是一个在线的数据结构，支持随时修改某个元素的值，复杂度也为log级别。

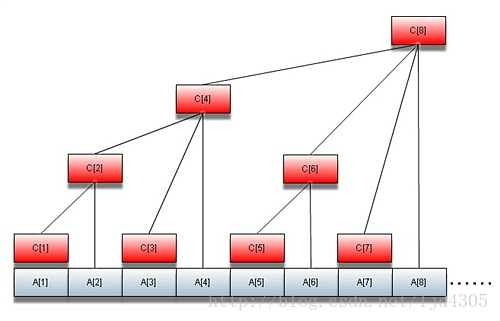
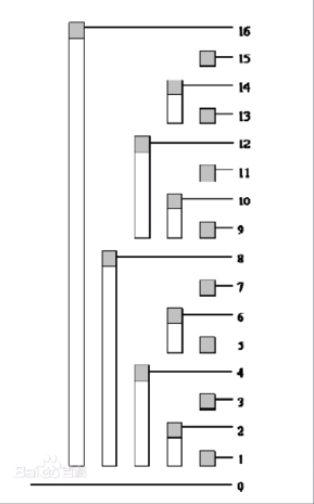
观察这棵树，容易发现：

　　C1 = A1

　　C2 = A1 + A2

　　C3 = A3

　　C4 = A1 + A2 + A3 + A4

　　C5 = A5

　　C6 = A5 + A6

　　C7 = A7

　　C8 = A1 + A2 + A3 + A4 + A5 + A6 + A7 + A8

　　......

　　C16 = A1 + A2 + A3 + A4 + A5 + A6 + A7 + A8 + A9 + A10 + A11 + A12 + A13 + A14 + A15 + A16

　　这里有一个有趣的性质：

　　设节点编号为x，那么这个节点管辖的区间为2^k（其中k为x二进制末尾0的个数）个元素。因为这个区间最后一个元素必然为Ax，

　　所以很明显：Cn = A(n – 2^k + 1) + ... + An

　　算这个2^k有一个快捷的办法，定义一个函数如下即可：

　　int lowerbit(int x){
　　　　return x&(x^(x–1));
　　}

 

　　利用机器补码特性，也可以写成：

　　int lowerbit(int x){
　　　    return x&-x;
　　}

　　当想要查询一个SUM(n)(求a[n]的和），可以依据如下算法即可：

　　step1:　令sum = 0，转第二步；

　　step2:　假如n <= 0，算法结束，返回sum值，否则sum = sum + Cn，转第三步；

　　step3: 令n = n – lowbit(n)，转第二步。

　　可以看出，这个算法就是将这一个个区间的和全部加起来，为什么是效率是log(n)的呢？以下给出证明：

　　n = n – lowbit(n)这一步实际上等价于将n的二进制的最后一个1减去。而n的二进制里最多有log(n)个1，所以查询效率是log(n)的。

　　那么修改呢，修改一个节点，必须修改其所有祖先，最坏情况下为修改第一个元素，最多有log(n)的祖先。

　　所以修改算法如下（给某个结点i加上x）：

　　step1: 当i > n时，算法结束，否则转第二步；

　　step2: Ci = Ci + x， i = i + lowbit(i)转第一步。

　　i = i +lowbit(i)这个过程实际上也只是一个把末尾1补为0的过程。

　　对于数组求和来说树状数组简直太快了!

　　注：

　　求lowbit(x)的建议公式：

　　lowbit(x):=x and -x;

　　或lowbit(x):=x and (x xor (x - 1));

　　lowbit(x)即为2^k的值。

 

以上对树状数组的解释来自百度百科，比较难以理解。

 

　　由图我们可以知道C8 是 A1+.....+A8，但是C6是 A5+A6，为什么要这么做？因为这样做会使操作更加简单，这样会使复杂度被log化。

C8可以看作A1......A8的左半边和+右半边和，而其中左半边和是C4，右半边其实也是同样的规则把a5......a8一分为二……继续下去都是一分为二直到不能分。树状数组也就是很巧妙的运用这种二分法来构建。

　　那么，怎么实现这种二分法？lowbit(k)就是把k的二进制的高位1全部清空，只留下最低位的1，比如10的二进制是1010，则lowbit(k)=lowbit(1010)=0010。

比较普遍的方法lowbit(k)=k&-k，这是位运算。我们知道一个数加一个负号是把这个数的二进制取反然后+1，如k=10时，-10的二进制就是-1010=0101+1=0110，然后k&-k就是1010&0110，答案就是0010了！这样就可以把A数组和C数组联系在一起，设节点编号为x，C(x)是A(x)往左连续求lowbit(k)个数的和，比如lowbit(0110)=0110&0010=0010=2。C[0110]=A[0110]+A[0101]。可以看到其实只有低位的1起作用，因为很显然可以写出c[0010]=a[0010]+a[0001]，这就为什么我们任何数都只关心它的lowbit，因为高位不起作用（基于我们的二分规则它必须如此！），除非除了高位其余位都是0，这时本身就是lowbit。

　　

void add(int k,int num) {
       while(k<=n) {
            tree[k]+=num;
            k+=k&-k;
        }
}

【题目链接】

Stars

Time Limit: 1000MS		Memory Limit: 65536K
Total Submissions: 45080		Accepted: 19567

• Description

Astronomers often examine star maps where stars are represented by points on a plane and each star has Cartesian coordinates. Let the level of a star be an amount of the stars that are not higher and not to the right of the given star. Astronomers want to know the distribution of the levels of the stars. 

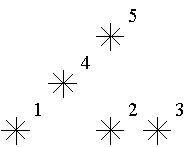
For example, look at the map shown on the figure above. Level of the star number 5 is equal to 3 (it's formed by three stars with a numbers 1, 2 and 4). And the levels of the stars numbered by 2 and 4 are 1. At this map there are only one star of the level 0, two stars of the level 1, one star of the level 2, and one star of the level 3.

You are to write a program that will count the amounts of the stars of each level on a given map.

• Input

The first line of the input file contains a number of stars N (1<=N<=15000). The following N lines describe coordinates of stars (two integers X and Y per line separated by a space, 0<=X,Y<=32000). There can be only one star at one point of the plane. Stars are listed in ascending order of Y coordinate. Stars with equal Y coordinates are listed in ascending order of X coordinate.

• Output

The output should contain N lines, one number per line. The first line contains amount of stars of the level 0, the second does amount of stars of the level 1 and so on, the last line contains amount of stars of the level N-1.

Sample Input

5
1 1
5 1
7 1
3 3
5 5

Sample Output

1
2
1
1
0

• Hint

This problem has huge input data,use scanf() instead of cin to read data to avoid time limit exceed.

【题意】

　　就是求每个小星星左小角的星星的个数。坐标按照Y升序，Y相同X升序的顺序给出 由于y轴已经排好序，可以按照x坐标建立一维树状数组。

#include <stdio.h>
#include <string.h>
const int MAXN=;
const int MINN=;
int tree[MAXN];//下标为横坐标
int level[MINN];//下标为等级数
/*int lowerbit(int x)
{
    return x&-x;
}*/
void add(int k,int num)
{
    while(k<=MAXN)
    {
        tree[k]+=num;
        k+=k&-k;
    }
}
int read(int k)//1~k的区间和
{
    int sum=;
    while(k)
    {
        sum+=tree[k];
        k-=k&-k;
    }
    return sum;
}
int main()
{
    int n,x,y,i;
    memset(tree,,sizeof(tree));
    memset(level,,sizeof(level));
    while(scanf("%d",&n)!=EOF)
    {
        for(i=;i<=n;i++)
        {
            scanf("%d%d",&x,&y);
            int temp=read(x+);//加入x+1，是为了避免0，X是可能为0的
            level[temp]++;
            add(x+,);
        }
        for(i=;i<n;i++)
            printf("%d\n",level[i]);
    }
    return ;
}