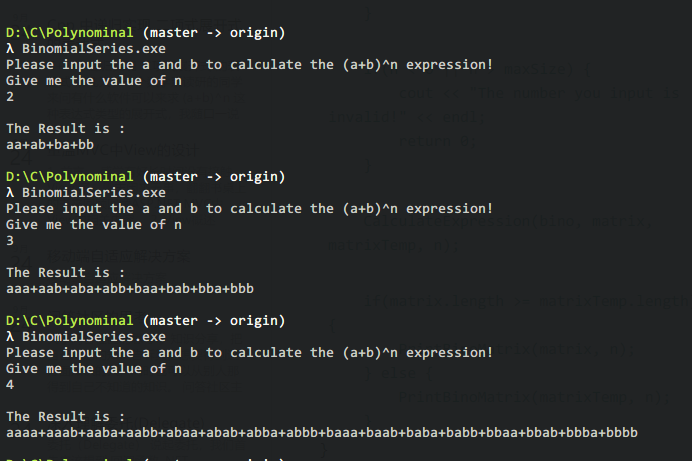
C++ 中递归实现 二项式展开式（a+b）^ n 的表达式

C++ 中递归实现 二项式展开式 的表达式

前几天，一个数学系读研的同学来问有什么软件可以来求 (a+b)^n 这种表达式类型的展开式，我随口一说了 Octave , 毕竟这个开源的还是可以的，后来他说了句 a 和 b 不一定是实数，那就很尴尬了。就是 a 和 b 仅代表符号。也可以是 (猫 + 狗)^n， 后来决定用CPP 来简单简单实现一下，由于对 CPP 不是很熟，搞了好一段时间，这个算法重点是递归。时间和空间复杂度略高了一点。

代码如下：

#include <iostream>
#include "string.h"
#include <iomanip>
#include <limits>
#include "tgmath.h"
#include <cmath>
#define maxSize 1000

using namespace std;

typedef struct Binomial {
   char array[maxSize];
   int length;
} Binomial;

typedef struct BinomialMatrix {
   string element[maxSize];
   int length;
} BinomialMatrix;

void CreateBinomial(Binomial &binomial, char a[], int length) {
   int i;

   for(i = 0; i < length; ++i) {
       binomial.array[i] = a[i];
   }

   binomial.length = length;
}

void PrintBinomialValue(Binomial binomial) {
   for(int i = 0; i < binomial.length; ++i) {
       cout << binomial.array[i] << " ";
   }

   cout << "\n" << endl;
}

void PrintBinoMatrix(BinomialMatrix matrix, int n) {
   int i;
   cout << "\n" << "The Result is :" << endl;

   int loopStart = matrix.length <= 2 ? 0 : 2;

   for(i = loopStart; i < matrix.length; ++i) {
       if(i == matrix.length - 1) {
           cout << matrix.element[i] << endl;
       } else {
           cout << matrix.element[i] << "+";
       }
   }
}

void CalculateExpression(Binomial binomial, BinomialMatrix &matrix,
                        BinomialMatrix &matrixTemp, int n) {
   int i, j, k = 0, t = 0, p = 0;

   if(n == 0) {
       matrix.element[n] = "1";
       matrix.length = 1;
       return;
   }

   matrix.element[k] = string(1, binomial.array[k]);
   matrix.element[k + 1] = string(1, binomial.array[k + 1]);
   matrix.length = 2;

   int loopLength = matrixTemp.length - matrix.length > 0 ? matrix.length : 0;

   if(matrixTemp.length < 10000) {
       for(i = 0; i < matrix.length; ++i) {
           for(j = loopLength; j < matrixTemp.length; ++j) {
               matrix.element[matrix.length + t] = matrix.element[i] + matrixTemp.element[j];
               ++t;
           }
       }

       matrix.length = matrix.length + t;
   }

   if(n >= 2) {
       CalculateExpression(binomial, matrixTemp, matrix, --n);
   }
}

int main() {
   int n;
   char a[] = "ab";

   Binomial bino;
   BinomialMatrix matrix;
   BinomialMatrix matrixTemp;

   CreateBinomial(bino, a, 2);

   cout << "Please input the a and b to calculate the (a+b)^n expression!" << endl;
   cout << "Give me the value of n" << endl;

   while(!(cin >> n)) {
       cin.clear();
       cin.ignore(numeric_limits<streamsize>::max(), '\n');
       cout << "\nPlease type a number n:\t";
   }

   if(n < 0 || n > maxSize) {
       cout << "The number you input is invalid!" << endl;
       return 0;
   }

   CalculateExpression(bino, matrix, matrixTemp, n);

   if(matrix.length >= matrixTemp.length) {
       PrintBinoMatrix(matrix, n);
   } else {
       PrintBinoMatrix(matrixTemp, n);
   }
}