开发模型之V模型

1.模型目的：

V模型的目的在于改进软件开发的效率和效果。

2.常见理论性描述： 

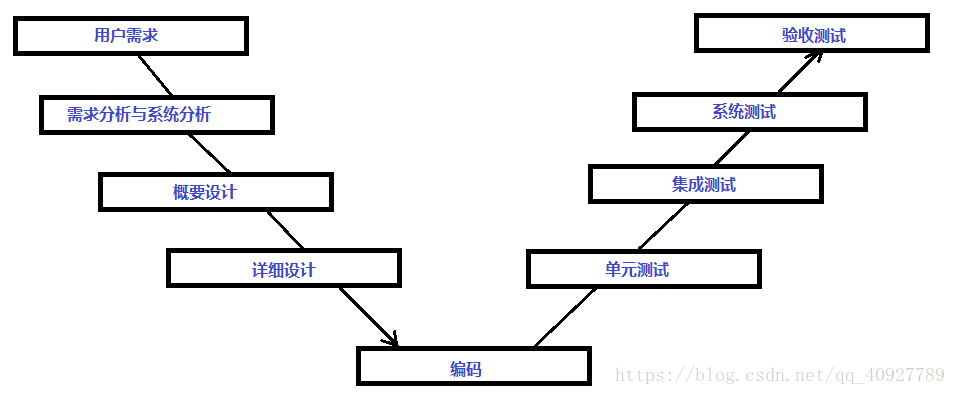
V模型从整体上看起来，就是一个V字型的结构，由左右两边组成。

左边的下划线分别代表了需求分析、概要设计、详细设计、编码，又称为软件开发生命周期 - SDLC；

右边的上划线代表了单元测试、集成测试、系统测试与验收测试，又称为软件测试生命周期 - STLC

看起来V模型就是一个对称的结构，它的重要意义在于，非常明确的表明了测试过程中存在的不同的级别，并且非常清晰的描述了这些测试阶段和开发阶段的对应关系，在每个软件开发阶段都有相应的测试阶段。V模型中的测试与SDLC阶段并行完成。

3.缺点：

在V模型中，只是把测试作为编码之后的一个阶段，并没有在需求开发阶段就进入测试。改进方法：在需求阶段和开发阶段，测试提前介入，并行工作。