df值自由度学习[转载]

转自：https://www.applysquare.com/topic-cn/78TAnIzZ6/

https://zhidao.baidu.com/question/1756050828556997148.html

1.简单说法

df是自由度的意思。

自由度指当以样本的统计量来估计总体的参数时， 样本中独立或能自由变化的自变量的个数，称为该统计量的自由度。

2.详解

在样本方差计算中，分母不是样本数量，而是样本量减一，人们一般认为减一是因为缺少一个自由度的原因，那么这个自由度的概念到底是什么？

2.1单样本t检验中：

如果一个数据集有10个值，10个值的总和必须等于 平均值x 10。如果10个值的均值为3.5(你可以选择任意数量)，这种约束要求10个值之和必须等于10 x 3.5 = 35。

有了这个约束，数据集的第一个值是可以自由变化的。对于任何值，所有10个数字值和对于35仍然是可能。 第二个值还可以自由变化因为无论你选择何种值，它仍然允许的可能性的总和为35。
事实上，前9个值可以是任何东西，包括这2个例子：
34, -8.3, -37, -92, -1, 0, 1, -22, 99
0.1, 0.2, 0.3, 0.4, 0.5, 0.6, 0.7, 0.8, 0.9但要有所有10个值的总和为35，并有一个平均值为3.5，第十个值不能改变。它必须是一个特定的数字：
34, -8.3, -37, -92, -1, 0, 1, -22, 99 -----> 10TH value must be 61.3
0.1, 0.2, 0.3, 0.4, 0.5, 0.6, 0.7, 0.8, 0.9 ----> 10TH value must be 30.5

因此你有10 - 1 = 9自由度，不管您使用什么样本量或者是你在使用样本平均值的最后一个值是不自由变化，你最终得到n- 1自由度其中n是样本容量。

2.2卡方检验：

一个卡方检验的独立性是用来确定两个分类变量是否相关。

对于这个测试，自由度是在两行和列的边际总数的约束条件下，可以改变的分类变量的双向表中的单元格数。所以每个“观察”在这种情况下是一个个体的频率。
考虑最简单的例子: : 一个2×2表，为每个类别的两类两水平。

不管使用什么值的行和列边际总数。一旦设置这些值，只有一个细胞的值可以改变(这里显示的标志可能是四个个体的任何一个)。一旦你输入一个个体的数量,所有其他个体的数量是预先的行和列的总数。 他们不是自由变化。因此，卡方检验的独立性自由度为1的2×2表。
类似地3 x 2表有2自由度，因为只有两个给定的一组细胞可以不同的边际总数。

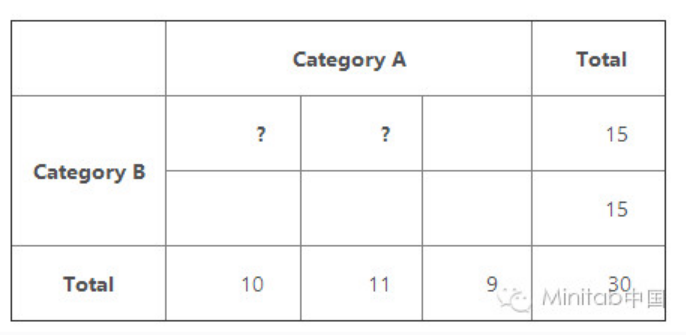
如果你尝试用不同大小的表，最终你会找到一个通用公式。对于一个r行和c列的表，可以改变个体的数量(r1)(c1)。
这就是独立的卡方检验的自由度公式。

//后面还讲到了回归过程中的自由度，这个我不太明白，就不放进来了。