随机模拟MCMC和Gibbs Sampling

随机模拟

统计模拟中有一个重要的问题就是给定一个概率分布

p(x)，我们如何在计算机中生成它的样本。一般而言均匀分布 Uniform(0,1)的样本是相对容易生成的。 通过线性同余发生器可以生成伪随机数，我们用确定性算法生成[0,1]之间的伪随机数序列后，这些序列的各种统计指标和均匀分布 Uniform(0,1) 的理论计算结果非常接近。这样的伪随机序列就有比较好的统计性质，可以被当成真实的随机数使用。

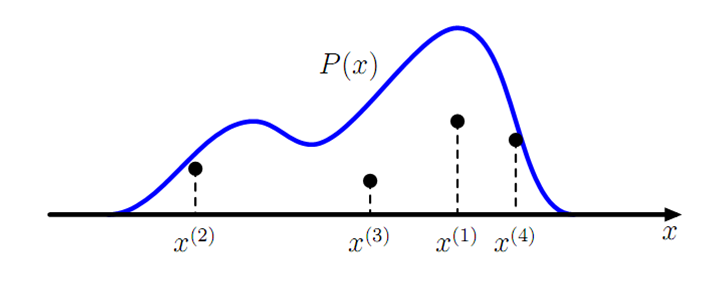
生成一个概率分布的样本

而我们常见的概率分布，无论是连续的还是离散的分布，都可以基于Uniform(0,1) 的样本生成。例如正态分布可以通过著名的 Box-Muller 变换得到

[Box-Muller 变换]  如果随机变量 U1,U2 独立且U1,U2∼Uniform[0,1]，

则Z0,Z1 独立且服从标准正态分布。

其它几个著名的连续分布，包括指数分布、Gamma 分布、t 分布、F 分布、Beta 分布、Dirichlet 分布等等,也都可以通过类似的数学变换得到；离散的分布通过均匀分布更加容易生成。更多的统计分布如何通过均匀分布的变换生成出来，大家可以参考统计计算 的书，其中 Sheldon M. Ross 的《统计模拟》是写得非常通俗易懂的一本。

不过我们并不是总是这么幸运的，当p(x)的形式很复杂，或者 p(x) 是个高维的分布的时候，样本的生成就可能很困难了。譬如有如下的情况：

此时就需要使用一些更加复杂的随机模拟的方法来生成样本。而本节中将要重点介绍的 MCMC(Markov Chain Monte Carlo) 和 Gibbs Sampling算法就是最常用的一种，这两个方法在现代贝叶斯分析中被广泛使用。要了解这两个算法，我们首先要对马氏链的平稳分布的性质有基本的认识。