[Algorithm] Delete a node from Binary Search Tree

The solution for the problem can be divided into three cases:

case 1: if the delete node is leaf node, then we can simply remove it

case 2: if the delete node is has single side or substree

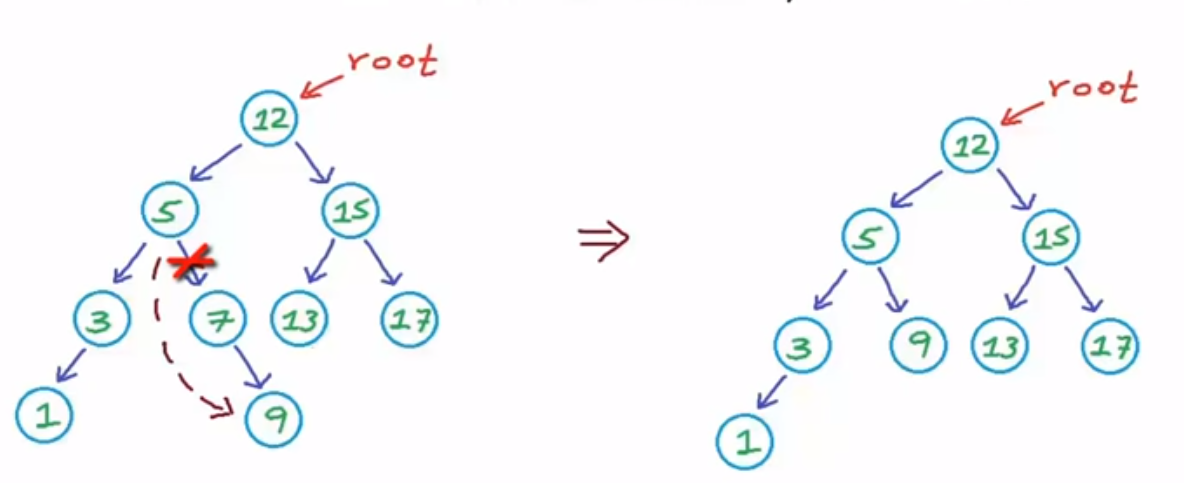
case 3: it has two children, then to keep it as a valid binary search tree, we can copy the min value from right subtree to delete node, to convert the problem into case 2

function Node(val) {
  return {
    val,
    left: null,
    right: null
  };
}

function Tree() {
  return {
    root: null,
    addLeft(val, root) {
      const node = Node(val);
      root.left = node;
      return root.left;
    },
    addRight(val, root) {
      const node = Node(val);
      root.right = node;
      return root.right;
    }
  };
}

const tree = new Tree();
const root = Node();
tree.root = root;
const n1 = tree.addLeft(, root);
const n2 = tree.addRight(, root);
const n3 = tree.addLeft(, n1);
const n4 = tree.addRight(, n1);
tree.addLeft(, n3);
tree.addRight(, n4);
const n5 = tree.addLeft(, n2);
tree.addRight(, n5);
const n6 = tree.addRight(, n2);
const n7 = tree.addRight(, n6);
tree.addLeft(, n7);

/**
 *
            12
          /    \
         5      15
       /  \    /  \
     3    7   13  17
    /      \    \   \
  1         9    14  20
                    /
                   18

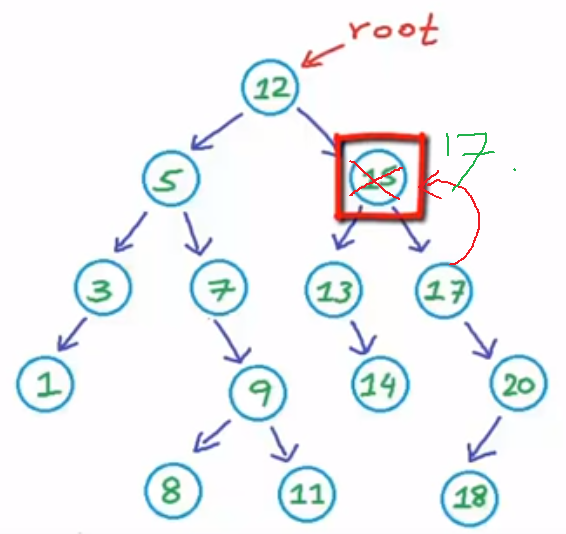
        Delete 15
    First copy 17 to 15
            12
          /    \
         5      17
       /  \    /  \
     3    7   13  17
    /      \    \   \
  1         9    14  20
                    /
                   18
     Then remove original 17
            12
          /    \
         5       17
       /  \    /   \
     3    7   13    20
    /      \   \   /
  1         9  14  18

 */

function deleteNode(root, val) {
  // base case, if leaf node, return
  if (root === null) {
    return root;
  } else if (val > root.val) {
    // if delete value is larger than root, search on right side of tree
    root.right = deleteNode(root.right, val);
  } else if (val < root.val) {
    // if delete value is smaller than root, search on left side of tree
    root.left = deleteNode(root.left, val);
  } else {
    // if found the delete value and it is leaf node
    if (root.left === null && root.right === null) {
      // set leaf node to null
      root = null;
    }
    // if found the delete node and its right side has children
    // set root to null and link to its right node
    else if (root.left === null && root.right !== null) {
      let temp = root.right;
      root = null;
      root = temp;
    }
    // if found the delete node and its left side and children
    // set root to null and link to its left node
    else if (root.left !== null && root.right === null) {
      let temp = root.left;
      root = null;
      root = temp;
    }
    // the found node has children on both sides
    // then pick the min value from rgiht side (or max value from left side)
    // copy to current node
    // reset it right side (or left side)
    else {
      const temp = root.right; // get the min on the right side or max on the left side
      root.val = temp.val;
      root.right = deleteNode(root.right, temp.val);
    }

    return root;
  }
}

deleteNode(tree.root, );

console.log(JSON.stringify(tree.root.left, null, ));