Codeforces Round #410 (Div. 2)C. Mike and gcd problem

题目连接：http://codeforces.com/contest/798/problem/C

C. Mike and gcd problem

time limit per test

2 seconds

memory limit per test

256 megabytes

input

standard input

output

standard output

Mike has a sequence A = [a1, a2, ..., an] of length n. He considers the sequence B = [b1, b2, ..., bn] beautiful if the gcd of all its elements is bigger than 1, i.e. .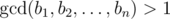

Mike wants to change his sequence in order to make it beautiful. In one move he can choose an index i (1 ≤ i < n), delete numbers ai, ai + 1 and put numbers ai - ai + 1, ai + ai + 1 in their place instead, in this order. He wants perform as few operations as possible. Find the minimal number of operations to make sequence A beautiful if it's possible, or tell him that it is impossible to do so.

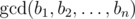 is the biggest non-negative number d such that d divides bi for every i (1 ≤ i ≤ n).

Input

The first line contains a single integer n (2 ≤ n ≤ 100 000) — length of sequence A.

The second line contains n space-separated integers a1, a2, ..., an (1 ≤ ai ≤ 109) — elements of sequence A.

Output

Output on the first line "YES" (without quotes) if it is possible to make sequence A beautiful by performing operations described above, and "NO" (without quotes) otherwise.

If the answer was "YES", output the minimal number of moves needed to make sequence A beautiful.

Examples

input

2
1 1

output

YES
1

input

3
6 2 4

output

YES
0

input

2
1 3

output

YES
1

Note

In the first example you can simply make one move to obtain sequence [0, 2] with .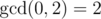

In the second example the gcd of the sequence is already greater than 1.

题解：我们发现一个位置经过两次操作a[i]变成-2a[i+1],a[i+1]变成2a[i],所以当gcd为1时我们可以把他们都变为偶数，所以我们把所有的数都变为偶数

#include<cstdio>
#include<iostream>
#include<cmath>
#include<cstring>
#include<algorithm>
using namespace std;
const int maxn=1e5+;
int a[maxn],n;
int main()
{
    scanf("%d",&n);
    for(int i=;i<n;i++)
    {
        scanf("%d",&a[i]);
    }
    int tmp=a[];
    for(int i=;i<n;i++)
    {
        tmp=__gcd(tmp,a[i]);
    }
    if(tmp!=)
    {
        puts("YES\n0");
    }
    else
    {
        int ans=;
        for(int i=;i<n;i++)
        {
            if(a[i]%==)continue;
            else if(i==n-)
            {
                ans+=;
            }
            else
            {
                if(a[i+]%!=)ans++;
                else ans+=;
                i++;
            }
        }
        printf("YES\n%d\n",ans);
    } 

}