3624: [Apio2008]免费道路

Description

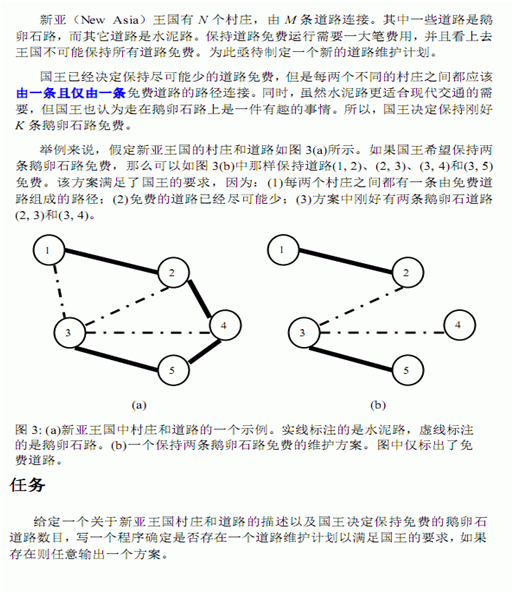
Input

Output

Sample Input

5 7 2

1 3 0

4 5 1

3 2 0

5 3 1

4 3 0

1 2 1

4 2 1

Sample Output

3 2 0

4 3 0

5 3 1

1 2 1

/*  比较优秀的一道题

我们对于这个K上来第一反应可能就是先找k个0，别的再说

但这个显然错误。（没准只有我个蒟蒻真试了=-=）

但是我们反过来想，如果c值为1的边和小于k条的c值为0的

边，能够使得这个图成立（即树）。那么我们将其中的一些c值

为1的边替换成c值为0的边，这个图还能成立。

证明我们可以这么想，首先我们已经搞出了一棵树，当我们

砍掉一条树枝时，就分成了两个树（这里一个点也看作一棵树），

即树a，树b，我们刚才砍了一条边，就要补一条边，补上的这

条边显然不可以是a中一点连a中另一点，b同理（万恶的并查集）

，那么只能是a中的某一点连到b中的某一点，那么此时它又变成

了一棵树。

同时还有一件事就是，对于c值为1的边，无论链接顺序怎样

最后连接的边数都是定值。（这里指用c值为1的边贪心的生成树）。

然后一切就都好办了，先贪心跑一遍c值为1的边，再在此基

础上跑c值为0的边（即最少需要c值为0的边的边数）。若此时不

能构成一颗完全的树，或者最少需要的c值为0的边的边数都大于

K显然无解。反之，我们把刚才用到的c值为0的边全部使用，再

补上剩下c值为0的边来满足K，如果不够k，无解。否则我们再跑

c值为1的就好了。

【注】 这个大视野卡回车啊！！！

 #include<cstdio>
 using namespace std;
 const int N=;
 struct edges{int u,v,c;}edge[N];
 int n,m,k;
 int stack[N],top;
 int beg[],ed[];
 int fa[N];
 bool chos[N];
 int find(int x){    return x==fa[x]?x:fa[x]=find(fa[x]);}
 int sum[];
 void solve(int op,int up){
     for(int i=;i<=m&&sum[op]<up;i++){
         if(edge[i].c==op){
             int u=edge[i].u,v=edge[i].v;
             u=find(u),v=find(v);
             if(u!=v){
                 sum[op]++;fa[v]=u;stack[++top]=i;chos[i]=true;
             }
         }
     }
 }

 void special(){
     for(int i=;i<=m;i++){
         if(edge[i].c==&&chos[i]){
             int u=edge[i].u,v=edge[i].v;
             u=find(u),v=find(v);
             if(u!=v){
                 fa[v]=u;
                 stack[++top]=i;
                 sum[]++;
             }
         }
     }
 }
 int main(){
     scanf("%d%d%d",&n,&m,&k);
     for(int i=;i<=m;i++){
         scanf("%d%d%d",&edge[i].u,&edge[i].v,&edge[i].c);
         }
     for(int i=;i<=n;i++)   fa[i]=i;
     solve(,N);
     solve(,N);
     if(sum[]+sum[]<n-||sum[]>k){
         printf("no solution\n");
         return ;
     }
     top=;
     for(int i=;i<=n;i++){fa[i]=i;}
     sum[]=sum[]=;
     special();
     solve(,k);
     if(sum[]<k)   {
         printf("no solution\n");return ;
     }
     solve(,n--k);
     for(int i=,j;i<=top;i++){
         j=stack[i];
             printf("%d %d %d\n",edge[j].u,edge[j].v,edge[j].c);
     }
 }