斯坦福【概率与统计】课程笔记（四）：EDA | 茎叶图

茎叶图的只做方法如下：

1. 将每个数字分成茎和叶
2. 对所有茎排序，并纵向从小到大放置好
3. 对相同茎下的叶归到一起并排序，垂直于茎的排列方向放置好

举个例子：我们有一份奥斯卡影后的年龄集合：

34 34 27 37 42 41 36 32 41 33 31 74 33 49 38 61 21 41 26 80 42 29 33 36 45 49 39 34 26 25 33 35 35 28 30 29 61 32 33 45 29 62 22 44

按照上述方法做出茎叶图：

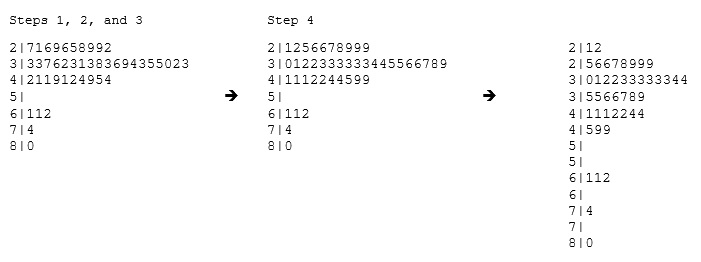
1. 上图中，先分析了一下年龄的数字，将个位数作为叶子，个位数之外的部分作为茎，所以茎的集合是：2、3、4、5、6、7、8；叶子的集合是所有个位数
2. 茎集合排序后垂直排列好，右侧画一条直线，以便和叶子区分
3. 每个茎下面的叶子从小到大排序，并垂直于茎的方向放置后（上图1和2）

上图的3的意思是：一些软件如果发现茎下面叶子高度过大，会将每个茎劈成两半放置，其下面的叶子的0-4给子茎1，5-9给子茎2（其实就是进一步细分，用直方图类比就是：之前是每10岁作为一个group，后来变成每5岁作为一个group了，类比一下就应该很容易理解）

茎叶图和直方图有一点类似，但其比直方图好的一个点是：直方图实际上损失了一些详细信息（比如把21、22、25、26、27都归结成[20, 30)这个group后，就只知道这个group下面的样本个数，而不知道实际每个样本的真实值了）；而茎叶图保留了每个样本的真实值。

但茎叶图也有不好的地方：其制作比较复杂，一般只能用在小规模的数据集合上。

---

另外还有一种和茎叶图类似的图：dotplot（点状图）

其就是把茎叶图中的实际值变成了点