[Codeforces 1197E]Culture Code(线段树优化建图+DAG上最短路)

[Codeforces 1197E]Culture Code(线段树优化建图+DAG上最短路)

题面

有n个空心物品，每个物品有外部体积\(out_i\)和内部体积\(in_i\),如果\(in_i> out_j\),那么j就可以套在i里面。现在我们要选出n个物品的一个子集，这个子集内的k个物品全部套在一起，且剩下的物品都无法添加到这个子集中（没有空间塞进去）。定义浪费的空间为子集中空心的部分，即\(in_{i_1} + (in_{i_2} - out_{i_1}) + (in_{i_3} - out_{i_2}) + \dots + (in_{i_k} - out_{i_{k-1}})\)。求浪费空间最少的子集个数。

分析

(CF的官方题解为)

考虑建图，对于每个物品i，我们找到能套到i中的物品j,从i向j连一条边，边权为\(in_i-out_j\)。最后如果某个点入度为0，就从虚拟节点s向它连一条边权为0的边，出度为0就向虚拟节点t连一条边权为\(in_i\)的边。这样我们就得到了一个有向无环图。可以发现，DAG上s到t的每一条路径都对应着满足条件的一个子集，而路径的边权和就是子集浪费的空间。那么问题就转化为，求DAG上s到t的最短路径条数

首先直接建图复杂度\(O(n^2)\)肯定是会TLE的。发现如果把物品按\(out_i\)从小到大排序，那么可以连边的物品是一个连续区间[1,R]，R可以二分查找求出。可以用线段树优化建图。

我们将线段树看成一个有向图，每个线段树节点看成图上的一个点，[l,r]向[l,mid],[mid+1,r]连边，叶子节点[l,l]向原图上的节点l连边。对于从x向编号属于区间[L,R]的点连边，我们用类似线段树区间更新的方法，将[L,R]拆成许多个小区间，再直接向这些小区间暴力连边。

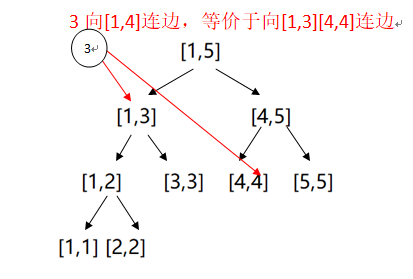
边权的问题如何解决？我们把边权\(in_i-out_j\)拆成两部分，叶子节点[l,l]向原图上的节点l连边权为\(-out_l\)的边，x向拆出来的边连边权为\(in_x\)的边。

最短路径数也很容易解决。记\(dist[x]\)表示s到x的最短路，\(cnt[x]\)表示s到x的最短路条数。初始时\(dist[s]=0,cnt[s]=1\),其他点\(dist[x]= +∞ ,cnt[x]=0 (x \neq s)\)

我们先对DAG拓扑排序,然后按照拓扑序，对每个节点x松弛它的出边，即若\(dist[y]>dist[x]+w(x,y)\)，就更新dist[y]。由于拓扑排序过，x会在y之前被更新，不会出现顺序问题。

然后类似的进行路径计数，求完最短路长度后，按照拓扑序对每个节点x做DP，如果\(dist[y]=dist[x]+w(x,y)\),那么\(cnt[y]+=cnt[x]\),最后的答案为\(cnt[t]\)

代码

#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>
#include<queue>
#define maxn 1000000
#define maxm 3000000
#define mod 1000000007
#define INF 0x3f3f3f3f
using namespace std;
typedef long long ll;
int n,new_n;
struct item{
	int in;
	int out;
	item(){

	}
	item(int _in,int _out){
		in=_in;
		out=_out;
	}
	friend bool operator < (item p,item q){
		if(p.out==q.out) return p.in<q.in;
		return p.out<q.out;
	}
}a[maxn+5];
int tmp[maxn+5]; 

struct edge{
	int from;
	int to;
	int len;
	int next;
}E[maxm*2+5];
int head[maxn+5];
int in[maxn+5];
int sz=1;
void add_edge(int u,int v,int w){
//	printf("%d->%d cost=%d\n",u,v,w);
	sz++;
	E[sz].from=u;
	E[sz].to=v;
	E[sz].len=w;
	E[sz].next=head[u];
	head[u]=sz;
	in[v]++;
}

ll dist[maxn+5];
ll cnt[maxn+5];

int seq[maxn+5];
void topo_sort(int s,int t){
	int len=0;
	queue<int>q;
	for(int i=s;i<=t;i++){
		if(!in[i]) q.push(i);
	}
	memset(dist,0x3f,sizeof(dist));
	dist[s]=0;
	while(!q.empty()){
		int x=q.front();
		q.pop();
		seq[++len]=x;
		for(int i=head[x];i;i=E[i].next){
			int y=E[i].to;
			in[y]--;
			if(!in[y]) q.push(y);
		}
	}
	for(int i=1;i<=len;i++){
		int x=seq[i];
		for(int i=head[x];i;i=E[i].next){
			int y=E[i].to;
			if(dist[y]>dist[x]+E[i].len) dist[y]=dist[x]+E[i].len;
		}
	}
	memset(cnt,0,sizeof(cnt));
	cnt[s]=1;
	for(int i=1;i<=len;i++){
		int x=seq[i];
		for(int i=head[x];i;i=E[i].next){
			int y=E[i].to;
			if(dist[y]==dist[x]+E[i].len){
				cnt[y]+=cnt[x];
				cnt[y]%=mod;
			}
		}
	}

}

struct segment_tree{
	struct tree_node{
		int l;
		int r;
	}tree[maxn*4+5];
	void build(int l,int r,int pos){
		tree[pos].l=l;
		tree[pos].r=r;
		if(l==r){
			new_n=max(new_n,pos+n);
			add_edge(pos+n,l,-a[l].out);
			return;
		}
		int mid=(l+r)>>1;
		add_edge(pos+n,(pos<<1)+n,0);
		add_edge(pos+n,(pos<<1|1)+n,0);
		build(l,mid,pos<<1);
		build(mid+1,r,pos<<1|1);
	}
	void update(int L,int R,int ux,int uv,int pos){
		if(L<=tree[pos].l&&R>=tree[pos].r){
			add_edge(ux,pos+n,uv);
			return;
		}
		int mid=(tree[pos].l+tree[pos].r)>>1;
		if(L<=mid) update(L,R,ux,uv,pos<<1);
		if(R>mid) update(L,R,ux,uv,pos<<1|1);
	}
}T;

ll cov[maxn+5];//统计每个节点可以被套的次数，如果cov[i]=0,则由s向i连边
int main(){
	scanf("%d",&n);
	new_n=0;
	new_n+=n;
	for(int i=1;i<=n;i++){
		scanf("%d %d",&a[i].out,&a[i].in);
		tmp[i]=a[i].out;
	}
	sort(a+1,a+1+n);
	sort(tmp+1,tmp+1+n);
	T.build(1,n,1);
	int s=0,t=new_n+1;
	for(int i=1;i<=n;i++){
		int rb=upper_bound(tmp+1,tmp+1+n,a[i].in)-tmp-1;
		if(rb>=1){
			cov[1]++;//差分统计，相当于[1,rb]+1
			cov[rb+1]--;
			T.update(1,rb,i,a[i].in,1);
		}else{
			add_edge(i,t,a[i].in);
		}
	}
	for(int i=1;i<=n;i++){
		cov[i]+=cov[i-1];
		if(cov[i]==0) add_edge(s,i,0);
	}
	topo_sort(s,t);
	printf("%I64d\n",cnt[t]);
}