清北学堂dp图论营游记day2

上午讲数位dp和背包问题。

先讲背包：

完全背包：换了个顺序：

多重背包：

多重背包优化：

这样把每个物品分成这些组，那么把他们转变成不同的物品，就变成了01背包问题；

滑动窗口取最值问题。单调队列优化。

方法很简单，枚举每一组中的其中一个物品计算即可。

小技巧：

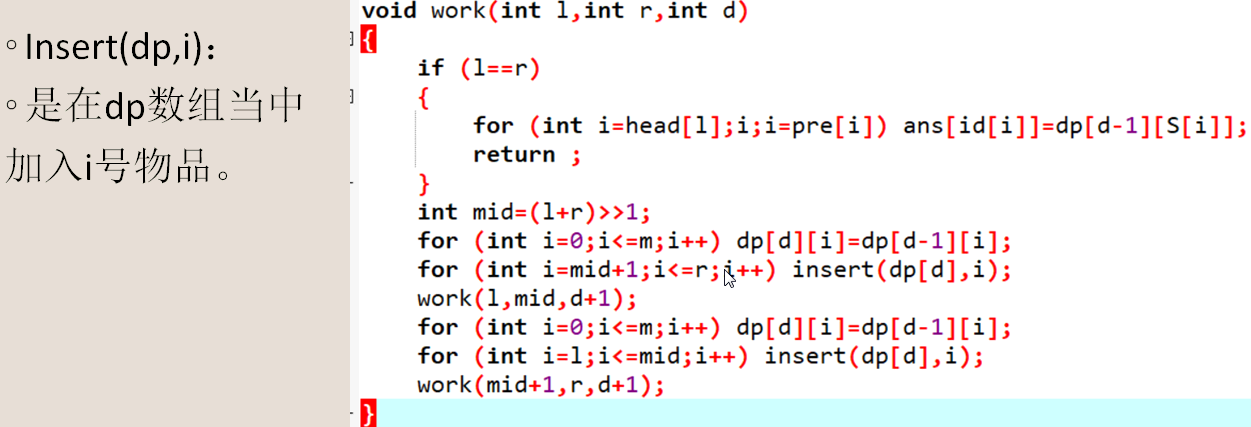
有些懵。。。

：

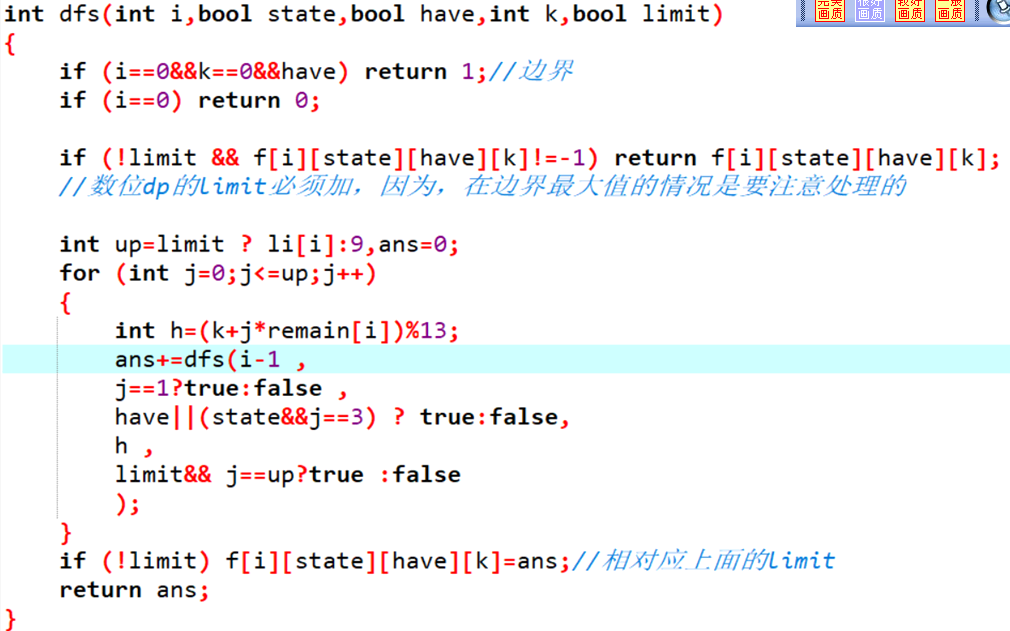
终于，到了数位dp环节：（恶心了一上午。）

dp方法：

判断上界。

假如我们要枚举到2147，当前已经枚举到了第二位，如果枚举到了1，那么我们说他达到了上界，下一位只能从0枚举到4。如果这一位是0，由于不管下一位是多少，这个数永远不可能大于原数，那么可以从0到9任意枚举。后几位也是如此。

下午：

接着讲树形dp:

前言

1：与树或图的生成树相关的动态规划。

2：以每棵子树为子结构，在父亲节点合并，注意树具有天然的子结构。

这是很优美的很利于dp的。

3：巧妙利用Bfs或Dfs序，可以优化问题，或得到好的解决方法。

4：可以与树上的数据结构相结合。

5：树形Dp的时间复杂度要认真计算，部分问题可以均摊复杂度分析。

6：一般设f[u]表示u子树的最优价值或者是说方案数。

或者f[u][k]表示u子树附加信息为k的最优值，往往是通过考虑子树根节点

的情况进行转移。 

第一题：

完结