cogs 2450. 距离 树链剖分求LCA最近公共祖先 快速求树上两点距离 详细讲解 带注释！

2450. 距离

★★   输入文件：distance.in   输出文件：distance.out   简单对比
时间限制：1 s   内存限制：256 MB

【题目描述】

在一个村子里有N个房子，一些双向的路连接着他们。人们总喜欢问这个“如果1想从房子A走到房子B有多远？”这个通常很难回答。但幸运的是在这个村里答案总是唯一的，自从道路修建以来这只有唯一的一条路（意思是你不能去一个地方两次）在每两座房子之间。你的工作是回答所有好奇的人。

【输入格式】

输入文件第一行有两个数n(2≤n≤10000)和m(1≤m≤20000),即房子数和问题数。后面n-1行每行由3个数构成i，j，k，由空格隔开，意思是房子i和房子j之间距离为k（0<k≤100）。房子以1到n标记。

下面m行每行有两个不同的整数i和j，你需要回答房子i和房子j之间的距离。

【输出格式】

输出有n行。每行表示个一个问题的答案。

【样例1】

输入样例1：
3 2
1 2 10
3 1 15
1 2
2 3
输出样例1：
10
25

【样例2】

输入样例2：
2 2
1 2 100
1 2
2 1
输出样例2：
100
100

【提示】

在此键入。

【来源】

在此键入。

本人决定：认真细致地讲一下树链剖分求LCA  以及快速地求树上两点的距离的方法

首先来讲解一下树链剖分的模板

1.首先要读入边 建边

根据具体的题目来决定是要建单向边还是双向边

2.两个dfs来进行树链剖分的预处理

3.写一下lca函数

4.询问+输出答案

这是一个非常巧妙的处理

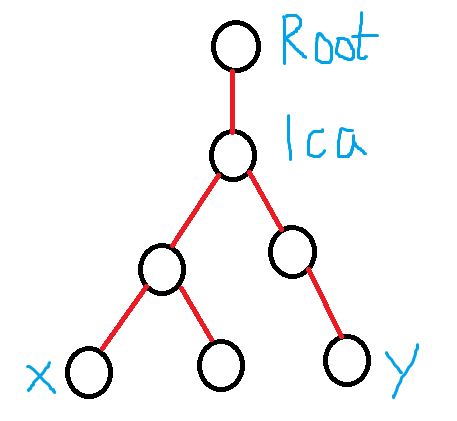
可以从上面的这一个图看出x到Root的距离 - lca到Root的距离  =  x到lca的距离

y到Root的距离   -   lca到Root的距离  =  y到lca的距离

两式合并得dis[x]  -  dis[lca]   +dis[y]  -  dis[lca]   =   x到y的距离

　　　　得出公式 dis[x]+dis[y]-2*dis[lca(x,y)]  =  x到y的距离

#include<bits/stdc++.h>
#define maxn 10005
using namespace std;
int n,q;
vector<int> v[maxn],w[maxn];
int size[maxn],dfn[maxn],pos[maxn],vis[maxn],fa[maxn],son[maxn],top[maxn],dep[maxn];
int cnt=;
int dis[maxn];
void Dfs(int x)
{
    size[x]=;//首先以x为根的子树的大小size  先设为1  就是目前已x为根的子树只有x自己
    for(int i=;i<v[x].size();i++)
    {
        int y=v[x][i];//son
        if(!size[y])//这里的意思其实就是如果这个儿子还没有访问过
        //因为我们可以看到每一次dfs的开始才会把size设一个数值 一开始应该都是0的
        //所以这里就可以直接当做一个vis标记用了
        {
            dep[y]=dep[x]+;//记录深度 son的深度 是father的深度+1
            fa[y]=x;//记录son的father 是谁
            dis[y]=dis[x]+w[x][i];//dis数组是存储每一个节点到根(1)的距离
            //son到根的距离就是father 到根的距离加上father和son之间的距离
            Dfs(y);
            size[x]+=size[y];//更新x为根的子树的大小
            if(size[son[x]]<size[y])//son存储的是重儿子
                son[x]=y;//更新重儿子
        }
    }
}
void Dfs(int x,int tp)
{
    top[x]=tp;//top数组是用来记录一条重链的顶端
    dfn[++cnt]=x;//dfn是记录第cnt个访问的点是x
    pos[x]=cnt;//pos记录第x个点是第cnt个访问的  当然在本题中不会用到
    if(son[x])//如果有重儿子 先走重儿子
        Dfs(son[x],tp);
    for(int i=;i<v[x].size();i++)
    {
        int y=v[x][i];
        if(!top[y])//走轻儿子
            Dfs(y,y);
    }
}
int lca(int x,int y)
{
    while(top[x]!=top[y])//先跳到同一条重链上
    {
        if(dep[top[x]]<dep[top[y]])
            swap(x,y);
        x=fa[top[x]];
    }
    if(dep[x]>dep[y])//保证x的深度更小  x就是lca
        swap(x,y);
    return x;
}
int main()
{
    freopen("distance.in","r",stdin);
    freopen("distance.out","w",stdout);
    scanf("%d%d",&n,&q);
    for(int i=;i<n;i++)
    {
        int x,y,z;
        scanf("%d%d%d",&x,&y,&z);
        v[x].push_back(y);
        w[x].push_back(z);
        v[y].push_back(x);
        w[y].push_back(z);
    }
    Dfs();Dfs(,);
    while(q--)
    {
        int x,y;
        scanf("%d%d",&x,&y);
        printf("%d\n",dis[x]+dis[y]-dis[lca(x,y)]*);
    }
    return ;
}