cf1282c

题意描述：

给你一颗带权无根树，共有2*n个节点，有n对人，然后每一个人被分配到一个节点上

问题1：怎么安排使得这n对人之间距离之和最小

问题2：怎么安排使得这n对人之间距离之和最大

题解：直接去想具体的方案根本无从下手，这里需要转换思维，我们去考虑每一条边对于答案的贡献，可以从下面这张图中找到答案，图来自官方题解

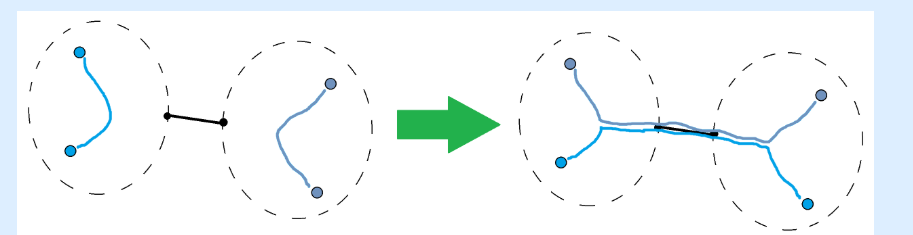
从图中可以看出，如果要最大化答案，那么我们会尽量的让点对不在同一个联通分量中，也就是尽量往两边走，可以证明这样一定是最优的

最小值把图左右两边换一下就好了

看了题解才会的，太巧妙了

#include<bits/stdc++.h>

#define forn(i, n) for (int i = 0 ; i < int(n) ; i++)
#define fore(i, s, t) for (int i = s ; i < (int)t ; i++)
#define fi first
#define se second
#define all(x) x.begin(),x.end()
#define pf2(x,y) printf("%d %d\n",x,y)
#define pf(x) printf("%d\n",x)
#define each(x) for(auto it:x)  cout<<it<<endl;
#define pi pair<int,int>

using namespace std;

char inline nc(){
    static char buf[100000],*p1=buf,*p2=buf;
    return p1==p2&&(p2=(p1=buf)+fread(buf,1,100000,stdin),p1==p2)?EOF:*p1++;
}

template <typename T>
bool rd(T& v){
    static char ch;
    while(ch!=EOF && !isdigit(ch)) ch=nc();
    if(ch==EOF) return false;
    for(v=0;isdigit(ch);ch=nc())
        v=v*10+ch-'0';
    return true;
}

template <typename T>
void o(T p){
    static int stk[70],tp;
    if(p==0) {
        putchar('0');return ;
    }
    if(p<0) {
        p=-p;putchar('-');
    }
    while(p) stk[++tp]=p%10,p/=10;
    while(tp) putchar(stk[tp--]+'0');
}

typedef long long ll;

const int maxn=2e5+5;
const int maxm=5e5+5;
const int inf=1e9;

int n,m;

int size[maxn];

int head[maxn],ver[maxm],nex[maxm],wi[maxm],tot;

void inline AddEdge(int x,int y,int z){
	ver[++tot]=y,nex[tot]=head[x],wi[tot]=z,head[x]=tot;
}

ll mn=0,mx=0;

void dfs(int x,int pa){
	size[x]=1;
	for(int i=head[x];i;i=nex[i]){
		int y=ver[i];
		if(y!=pa) {
			dfs(y,x);
			size[x]+=size[y];
			mn+=1ll*wi[i]*(size[y]%2);
			mx+=1ll*wi[i]*min(size[y],2*n-size[y]);
		}
	}
}

void solve(){
	tot=0;
	cin>>n;
	m=2*n-1;
	for(int i=1;i<=2*n+1;i++)
		head[i]=0;
	for(int i=0;i<m;i++){
		int x,y,z;
		scanf("%d%d%d",&x,&y,&z);
		AddEdge(x,y,z);
		AddEdge(y,x,z);
	}
	mn=0,mx=0;
	dfs(1,0);
	printf("%lld %lld\n",mn,mx);
}

int main(){
	int t;
	cin>>t;
	while(t--)
		solve();
}