AdaBoost笔记之原理

转自：https://www.cnblogs.com/ScorpioLu/p/8295990.html

一、Boosting提升算法

AdaBoost是典型的Boosting算法，属于Boosting家族的一员。在说AdaBoost之前，先说说Boosting提升算法。Boosting算法是将“弱学习算法“提升为“强学习算法”的过程，主要思想是“三个臭皮匠顶个诸葛亮”。一般来说，找到弱学习算法要相对容易一些，然后通过反复学习得到一系列弱分类器，组合这些弱分类器得到一个强分类器。

Boosting算法要涉及到两个部分，加法模型和前向分步算法。

加法模型就是说强分类器由一系列弱分类器线性相加而成。一般组合形式如下：

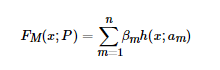
其中，h(x;a_m) 就是一个个的弱分类器，a_m是弱分类器学习到的最优参数，β_m就是弱学习在强分类器中所占比重，P是所有a_m和β_m的组合。这些弱分类器线性相加组成强分类器。

前向分步就是说在训练过程中，下一轮迭代产生的分类器是在上一轮的基础上训练得来的。也就是可以写成这样的形式：

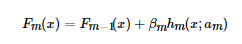
由于采用的损失函数不同，Boosting算法也因此有了不同的类型，AdaBoost就是损失函数为指数损失的Boosting算法。

二、AdaBoost

原理理解

基于Boosting的理解，对于AdaBoost，我们要搞清楚两点：

每一次迭代的弱学习h(x;a_m)有何不一样，如何学习？
弱分类器权值β_m如何确定？

对于第一个问题，AdaBoost改变了训练数据的权值，也就是样本的概率分布，其思想是将关注点放在被错误分类的样本上，减小上一轮被正确分类的样本权值，提高那些被错误分类的样本权值。然后，再根据所采用的一些基本机器学习算法进行学习，比如逻辑回归。

对于第二个问题，AdaBoost采用加权多数表决的方法，加大分类误差率小的弱分类器的权重，减小分类误差率大的弱分类器的权重。这个很好理解，正确率高分得好的弱分类器在强分类器中当然应该有较大的发言权。

实例

为了加深理解，我们来举一个例子。

有如下的训练样本，我们需要构建强分类器对其进行分类。x是特征，y是标签。

序号	1	2	3	4	5	6	7	8	9	10
x	0	1	2	3	4	5	6	7	8	9
y	1	1	1	-1	-1	-1	1	1	1	-1

令权值分布D1=(w₁_,₁,w₁_,₂,…,w₁_,₁₀)

并假设一开始的权值分布是均匀分布：w₁_,_i=0.1，i=1,2,…,10

现在开始训练第一个弱分类器。我们发现阈值取2.5时分类误差率最低，得到弱分类器为：

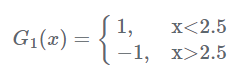
当然，也可以用别的弱分类器，只要误差率最低即可。这里为了方便，用了分段函数。得到了分类误差率e1=0.3。

第二步计算G1(x)在强分类器中的系数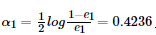，这个公式先放在这里，下面再做推导。

第三步更新样本的权值分布，用于下一轮迭代训练。由公式：

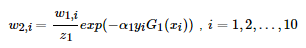
得到新的权值分布，从各0.1变成了：

D2=(0.0715,0.0715,0.0715,0.0715,0.0715,0.0715,0.1666,0.1666,0.1666,0.0715)

可以看出，被分类正确的样本权值减小了，被错误分类的样本权值提高了。

第四步得到第一轮迭代的强分类器：

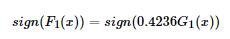
以此类推，经过第二轮……第N轮，迭代多次直至得到最终的强分类器。迭代范围可以自己定义，比如限定收敛阈值，分类误差率小于某一个值就停止迭代，比如限定迭代次数，迭代1000次停止。

这里数据简单，在第3轮迭代时，得到强分类器：

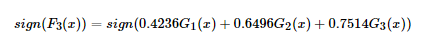
的分类误差率为0，结束迭代。

F(x)=sign(F3(x))就是最终的强分类器。

算法流程

总结一下，得到AdaBoost的算法流程：

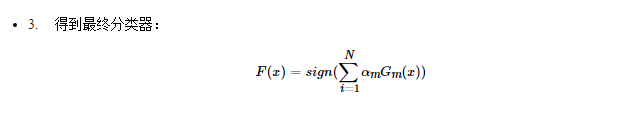
公式推导

现在我们来搞清楚上述公式是怎么来的。

真漂亮！

另外，AdaBoost的代码实战与详解请戳代码实战之AdaBoost

还可参考：机器学习实战之AdaBoost算法