（原创）白话KMP算法详解

引子：BF暴力算法

KMP算法知名度相当高，燃鹅其理解难度以及代码实现对于初学数据结构和算法的同学并不友好，经过两天的总结，详细总结KMP算法如下：

初学串的模式匹配时，我们都会接触到，或者说应该能想到作为教学引子的BF暴力算法，那么先来简单了解一哈：

我有一个大串是"abccabca",小串是"bca",现在要找到小串在大串中的位置,战斗开始

①

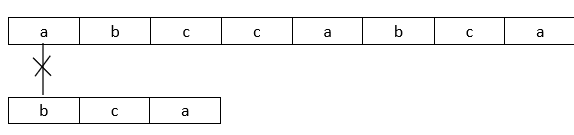
②

③

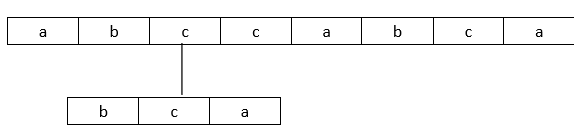
④

⑤

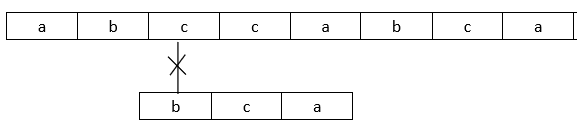
⑥

⑦

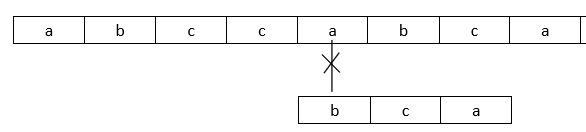
⑧

这个算法理解起来肥肠简单，我在这里假定 i 指针指向大串（主串）的首地址，j 指针指向小串（模式串）的首地址。首先大串第一位正面对比小串第一位，两元素若相等，则两指针分别后移，继续比较第二位。那么这个算法被称为暴力算法的原因就在于当两串元素对比不相等时，j指针就会回溯到小串的首地址，这本无可厚非，而i指针却会回溯到对比之初的后一位，比如上述第四步大小串匹配不上之后i指针马上来到了第三位，导致了完全无用的第五和第六步比较，造成了算法时间复杂度的加大，而且主串元素数嵌套小串元素数的两重循环，直接造成了O（m*n）的人间大惨案。虽然能实现模式匹配，但是我们的D.E.Knuth、J.H.Morris和V.R.Pratt觉得这个算法有必要改进一哈（V.R.Pratt：嘤嘤嘤），而且出于科学家的身份和*友情缘，三位同时研究出了一个船（全）新的匹配方式，KMP算法横空出世，当然只要体验三分钟，你就会跟我当时一样，放弃这个算法。

附：BF暴力算法代码（取自《大话数据结构》   ps： S[0]、T[0]表示该串的长度）

第一章：kmp算法

黄历上写明了，这个算法不宜先学代码，否则可能会造成理解困难。我这里还是先以一个例子来讲解一下这三个外国同学的算法：

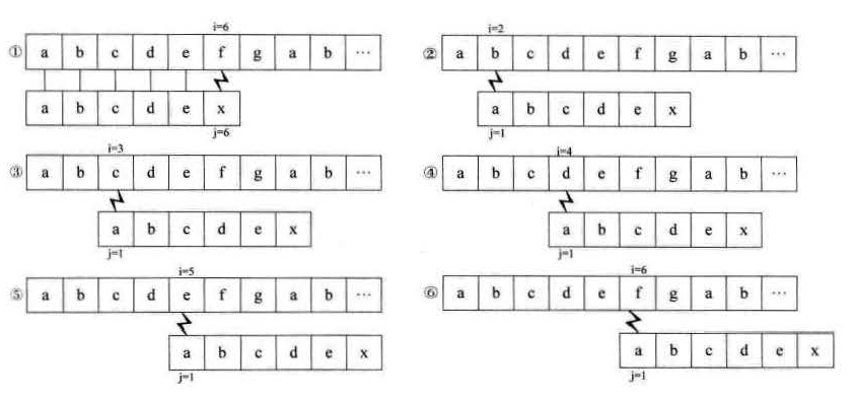(例子取自《大话数据结构》)

不难发现，我们的模式串没有一个字母是重复出现的，而第一步已经确诊主串和模式串的前五位一模一样，所以你如果这时候使用BF暴力算法，依次用主串的第二位到第五位跟模式串的首位正面刚，就是人傻劲大，完全莫得必要。所以我们要想个办法避免这种重复浪费的现象，结合上面的BF例子，我们也可以明白，这种现象的出现并非是 j 指针的错，而是 i 指针作为主串的指针瞎回溯造成的匹配浪费。

好的，理解了上面的步骤为啥子是多余的，我们再次征讨一下曾被我们用了很长一段时间的暴力算法，正因为它能力有限，只能通过把 i 回溯到一个很靠前的位置才能实现匹配，重点来了，这时来了一个叫做KMP的人，告诉你BF能做到的他也能做到，甚至能把时间复杂度降为O（m+n），这个时间复杂度是什么概念，意味着 i 再也不用承受眼看着无用还不得不回溯的命运。我们来看看KMP算法是怎样干掉BF这个老黄牛的。（前方高能，佩戴脑子食用效果更佳）

要想 i 值不回溯，就一定要在 j 上面做文章，我们再次看看上面的例子，如果第一步刚发现 i=6 两串不匹配时，摁住 i 指针，让 i 继续=6 ，然后这时候使j指针回到初始的位置，即 i = 6 时 j = 1，让主串中的 f 和模式串的 a 比较，就很完美辽，那这里也可能有机智的同学问，要是我的模式串中出了一个和首元素相等的元素怎么破？（/手动狗头），不妨看看这个例子，主串是 "abcabcabx", 模式串是 "abcabx" ，当然贼符合你的心意，当用BF第一轮比到第六位，发现 c 和 x 不一样，这时你会想，把 i 回溯到第四个元素（即 a），再用 j = 1 直接就出结果。但是你想一想，可否不移动 i ,让 j = 3 直接匹配，况且这个例子只是特殊情况，所以怎样看来都是不必回溯 i 的，下面我们看看怎样让 j 发挥他的作用。

既然是 j 的事，就和主串没关系了，我们来研究一下上一段这个例子，我们刚才为什么要移动 j 让他等于3，为了省去模式串前面存在的重复比较，这个重复比较是哪来的呢，就在于 模式串结构中的前后重复程度， "abcabx"这个例子中的串可以分为 "a"+"bcabx" 、"ab"+"cabx"、"abc"+"abx"、"abca"+"bx"、"abcab"+"x"，前缀有"a"、"ab"、"abc"、"abca"、"abcab"，定义第一个前缀重复度为0，第二个前缀重复度为1，第三个也是1，第四个我们不难发现首尾呼应，所以他的重复度较前面的加一是2，最后一个前缀ab段重复，故重复度为3。

那我们求出这个重复度有毛用呢，我们再看看那个例子，当我们在第一轮发现第六个不相等时，我们可以发现前五位重复度为3，这个3眼熟不，他可以直接在 i 不回溯的前提下把 j 带到正确的位置，即 j = 3，那我们模式串的每一个数都需要这个值来实现KMP算法，我们用一个 next[x] 数组来储存这些数，至于x的大小取决于你的模式串长度。

这时候我们来看看KMP算法的代码（当然还是来自《大话数据结构》的伪码）：

这段代码是获得 next数组 的

敲了芥末多的字，希望大家可以快速理解这个KMP模式匹配算法，未完待续.......

预告第二章：KMP算法的改进版本

届时神秘的nextval数组将浮现江湖

continued