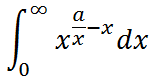洛谷4525 & 4526:【模板】自适应辛普森法——题解
参考:https://phqghume.github.io/2018/05/19/%E8%87%AA%E9%80%82%E5%BA%94%E8%BE%9B%E6%99%AE%E6%A3%AE%E6%B3%95/ 以及洛谷不多的题解。
辛普森推导过程就看参考吧,当然你要想看懂推导需要:
1.会高中导数那点东西,至少知道原函数怎么求。
2.粗略了解定积分。
3.知道微积分第一、第二基本定理(从知乎上找的:https://www.zhihu.com/question/21439225)。
然后推导就很简单了,实际上就是用的是将任意曲线近似转换成二次函数曲线去求。
————————————————————
https://www.luogu.org/problemnew/show/P4525
计算积分
结果保留至小数点后6位。
数据保证计算过程中分母不为0且积分能够收敛。
这就是自适应辛普森的板题了,eps开到1e-12大概就能过了。
(话说为什么要“自适应”?那当然是因为精度的原因啦,我们左右分一下将答案求和和一个区间的答案比较一下没有多少误差就return就行啦。)
#include<cmath>
#include<queue>
#include<cstdio>
#include<cctype>
#include<cstring>
#include<iostream>
#include<algorithm>
using namespace std;
typedef double dl;
const dl eps=1e-;
dl a,b,c,d,L,R;
inline dl f(dl x){
return (c*x+d)/(a*x+b);
}
inline dl simpson(dl l,dl r){
dl mid=(l+r)/;
return (f(l)+*f(mid)+f(r))*(r-l)/;
}
inline dl asr(dl l,dl r,dl ans){
dl mid=(l+r)/;
dl l1=simpson(l,mid),r1=simpson(mid,r);
if(fabs(l1+r1-ans)<eps)return l1+r1;
return asr(l,mid,l1)+asr(mid,r,r1);
}
int main(){
scanf("%lf%lf%lf%lf%lf%lf",&a,&b,&c,&d,&L,&R);
printf("%lf\n",asr(L,R,simpson(L,R)));
return ;
}
————————————————————
https://www.luogu.org/problemnew/show/P4526
计算积分
保留至小数点后5位。若积分发散,请输出"orz"。
挺吓人的,但思考a<0显然就发散了。
a>=0时a越大收敛得越慢,于是打表,大概得出来x=12时就已经约为0了。
于是L=eps,R=12跑一遍自适应辛普森法即可。
#include<cmath>
#include<queue>
#include<cstdio>
#include<cctype>
#include<cstring>
#include<iostream>
#include<algorithm>
using namespace std;
typedef double dl;
const dl eps=1e-;
dl a;
inline dl f(dl x){
return pow(x,a/x-x);
}
inline dl simpson(dl l,dl r){
dl mid=(l+r)/;
return (f(l)+*f(mid)+f(r))*(r-l)/;
}
inline dl asr(dl l,dl r,dl ans){
dl mid=(l+r)/;
dl l1=simpson(l,mid),r1=simpson(mid,r);
if(fabs(l1+r1-ans)<eps)return l1+r1;
return asr(l,mid,l1)+asr(mid,r,r1);
}
int main(){
scanf("%lf",&a);
if(a<)puts("orz");
else printf("%.5lf\n",asr(eps,,simpson(eps,)));
return ;
}
+++++++++++++++++++++++++++++++++++++++++++
+本文作者:luyouqi233。 +
+欢迎访问我的博客:http://www.cnblogs.com/luyouqi233/+
+++++++++++++++++++++++++++++++++++++++++++
洛谷4525 & 4526:【模板】自适应辛普森法——题解的更多相关文章
- 洛谷 P4525 & P4526 [模板] 自适应辛普森积分
题目:https://www.luogu.org/problemnew/show/P4525 https://www.luogu.org/problemnew/show/P4526 学习辛普森积分:h ...
- 洛谷P3387 【模板】缩点 题解
背景 今天\(loj\)挂了,于是就有了闲情雅致来刷\(luogu\) 题面 洛谷P3387 [模板]缩点传送门 题意 给定一个\(n\)个点\(m\)条边有向图,每个点有一个权值,求一条路径,使路径 ...
- 洛谷.4525.[模板]自适应辛普森法1(Simpson积分)
题目链接 Simpson积分公式:\[\int_a^bf(x)dx\approx\frac{b-a}{6}\left[f(a)+f(b)+4f(\frac{a+b}{2})\right]\] 推导过程 ...
- 洛谷 P3385 【模板】负环 题解
P3385 [模板]负环 题目描述 暴力枚举/SPFA/Bellman-ford/奇怪的贪心/超神搜索 寻找一个从顶点1所能到达的负环,负环定义为:一个边权之和为负的环. 输入格式 第一行一个正整数T ...
- 洛谷P4526 【模板】自适应辛普森法2
P4526 [模板]自适应辛普森法2 洛谷传送门 题目描述 计算积分 保留至小数点后5位.若积分发散,请输出"orz". 输入格式 一行,包含一个实数,为a的值 输出格式 一行,积 ...
- 洛谷P4525 【模板】自适应辛普森法1与2
洛谷P4525 [模板]自适应辛普森法1 与P4526[模板]自适应辛普森法2 P4525洛谷传送门 P4525题目描述 计算积分 结果保留至小数点后6位. 数据保证计算过程中分母不为0且积分能够收敛 ...
- P4526 【模板】自适应辛普森法2
P4526 [模板]自适应辛普森法2 #include <bits/stdc++.h> using namespace std; ; double a; inline double f(d ...
- P4525 【模板】自适应辛普森法1
P4525 [模板]自适应辛普森法1 #include <bits/stdc++.h> using namespace std; ; double a, b, c, d, l, r; in ...
- FFT/NTT总结+洛谷P3803 【模板】多项式乘法(FFT)(FFT/NTT)
前言 众所周知,这两个东西都是用来算多项式乘法的. 对于这种常人思维难以理解的东西,就少些理解,多背板子吧! 因此只总结一下思路和代码,什么概念和推式子就靠巨佬们吧 推荐自为风月马前卒巨佬的概念和定理 ...
随机推荐
- Ubuntu Server 下将HTML页面转换为PNG图片
零.前言 最近做一个网站,需要将网页转换为图片.由于服务器是Ubuntu Server,没有图形界面,所以实现的过程中遇到了很多问题.记录下来备用. 一.安装CutyCapt CutyCapt是一个可 ...
- unity面试题二
1.以下哪一个选项不属于Unity引擎所支持的视频格式文件(D) A.后缀为mov的文件 B.后缀为mpg的文件 C.后缀为avi的文件 D.后缀为swf的文件 2.Unity引擎使用的是左手坐标系还 ...
- 2019年猪年海报PSD模板-第五部分
14套精美猪年海报,免费猪年海报,下载地址:百度网盘,https://pan.baidu.com/s/1CuZKPmFbbSBvzSXoCt2few
- Appium Inspector定位元素与录制简单脚本
本次以微信为例, 使用Appium自带的Inspector定位工具定位元素, 以及进行最最最简单脚本的录制: capabilities = { "platformName": &q ...
- 关于Python 中的 if 语句
学习Python,最开始我们都是先从函数学起,Python教程中有很多函数,if算是其中之一. 可能最为人所熟知的编程语句就是 if 语句了.例如: >>> >>> ...
- redis集群搭建(伪集群)
1.准备工作 去官网下载好你想要安装的redis版本,下载链接 2.搭建步骤 输入命令yum install gcc-c++安装好gcc环境,将下载好的redis安装包上传到 /usr/local 解 ...
- 天平 (Not so Mobile UVA - 839)
题目描述: 题目思路: 1.DFS建树 2.只有每个树的左右子树都平衡整颗树才平衡 #include <iostream> using namespace std; bool solve( ...
- [转载]Tensorflow中reduction_indices 的用法
Tensorflow中reduction_indices 的用法 默认时None 压缩成一维
- 官方文档 恢复备份指南三 Recovery Manager Architecture
本节讨论以下问题: About the RMAN Environment 关于RMAN环境 RMAN Command-Line Client ...
- mysql mariadb 密码设置
原文:https://my.oschina.net/uyunsky/blog/109532 一.初始安装 Method 1:在/usr/local/mysql/bin/下:./mysqladmin - ...