动态规划初级 入门理解 C#代码

 

using System;
using System.Collections.Generic;
using System.Linq;
using System.Text;

using Microsoft.Practices.EnterpriseLibrary.Validation.Validators;
using Microsoft.Practices.EnterpriseLibrary.Validation;

namespace ConsoleApplication1
{
    class Program
    {
        static void Main(string[] args) {

            int[] arr = new int[] {10,5,3,6,8,9,7};
            int[] recode = new int[arr.Length];
            recode[0] = 1;
            //求数组中最长非降 子序列
            for (int i = 1; i < arr.Length; i++)
            {
                if (arr[i] > arr[i - 1])
                    recode[i] = recode[i-1]+1;
                else
                    recode[i] = recode[i-1];

            }
            for (int i = 0; i <  recode.Length ; i++)
            {
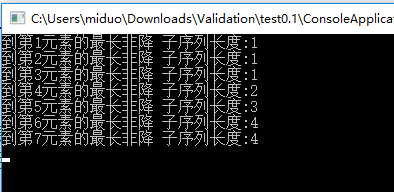
                Console.WriteLine("到第"+(i+1)+"元素的最长非降 子序列长度:"+recode[i]);
            }
            Console.Read();

        }
    }

}

　　执行结果 :这里保存了到某个长度下的所有状态 如果不需要 完全可以用int变量存储 不需要使用数组 这样复杂度分别为 o(n),o(1)

　

问题

一个序列有N个数：A[1],A[2],…,A[N]，求出最长非降子序列的长度

　分析 我先用列举法考虑简单情况 然后找规律

　　第一个元素最长非降序列长度肯定为1 因为只有本身 没有比较对象 记为 f(1)=1

　　到第二个元素 与第一个元素进行对比 如果小于第一个元素 那么这里第二个元素并没有为长度做出贡献 状态还保持在上一个元素 记 f(2)=1=f(1)

　　以此类推

　　最后得到以上结果

　　

这是我对动态规划的入门理解 即之前最优的状态影响着当前状态 而上一个状态就是在这之前的最优状态  这样也能降低算法的复杂程度

第二例

代码

　　

using System;
using System.Collections.Generic;
using System.Linq;
using System.Text;

using Microsoft.Practices.EnterpriseLibrary.Validation.Validators;
using Microsoft.Practices.EnterpriseLibrary.Validation;

namespace ConsoleApplication1
{
    public class NodeDistance
    {
        /// <summary>
        /// 节点名称
        /// </summary>
        public string nodeName { get; set; }
        /// <summary>
        /// 能到达的节点及与他们的距离列表
        /// </summary>
        public List<(string nodeName, int distance)> distance { get; set; }

    }
    class Program
    {
        //记录已到达的（走到当前的）最短路径
        static (string lujin, int distance) luxianDaoDa = ("", int.MaxValue);

        static void Main(string[] args)
        {

            //  问题 无向图上有N(1<N)个节点 每个节点有任意长的距离 计算任意节点A到任意节点B的距离
            //使用二维数组模拟点的情况 以及单个点到其他点的距离 先从简单的情况开始考虑 有abcd四个节点 每个节点可以到达其他节点

            List<NodeDistance> nodeList = new List<NodeDistance>() {
                new NodeDistance
                {
                     nodeName="a",
                      distance=new List<(string nodeName, int distance)>{
                          ("b",2),("c",7),("c",7)
                      }
                },
                new NodeDistance
                {
                     nodeName="b",
                      distance=new List<(string nodeName, int distance)>{
                          ("a",2),("c",3),("d",2)
                      }
                },
                   new NodeDistance
                {
                     nodeName="c",
                      distance=new List<(string nodeName, int distance)>{
                          ("a",7),("d",5),("b",3)
                      }
                },
                        new NodeDistance
                {
                     nodeName="d",
                      distance=new List<(string nodeName, int distance)>{
                          ("a",6),("c",3),("b",2)
                      }
                },

            };
            List<(string lujin, int distance)> luxian = new List<(string lujin, int distance)>();

            //求a-c得最短路径
            CalcDistance("a", "c", "a", 0, nodeList);
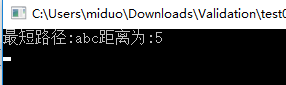
            Console.WriteLine("最短路径:" + luxianDaoDa.lujin + "距离为:" + luxianDaoDa.distance);
            Console.Read();

        }

        /// <summary>
        /// 计算距离
        /// </summary>
        /// <param name="node">当前节点</param>
        /// <param name="endChar">结束位置</param>
        public static void CalcDistance(string startChar, string endChar, string luxianName, int distance, List<NodeDistance> nodeList)
        {
            var node = nodeList.Where(u => u.nodeName == startChar).FirstOrDefault();
            //记录走过的节点
            foreach (var item in node.distance)
            {
                //判断当前节点是否走过 或者是否为起点
                if (item.nodeName == "a") continue;
                luxianName += item.nodeName;
                // 判断是否为当前情况下的最优状态  如果是 判断是否为终点
                distance += item.distance;
                if (distance >= luxianDaoDa.distance) continue;
                if (item.nodeName == endChar)
                    luxianDaoDa = (luxianName, distance);
                else
                    CalcDistance(item.nodeName
                        , endChar, luxianName, distance, nodeList);

            }

        }

    }

}

　　运行结果

　　

抽屉取苹果

using System;
using System.Collections.Generic;
using System.Linq;
using System.Text;

using Microsoft.Practices.EnterpriseLibrary.Validation.Validators;
using Microsoft.Practices.EnterpriseLibrary.Validation;

namespace ConsoleApplication1
{

    class Program
    {

        static int[][] apple = new int[3][];
        static int[][] appleSum = new int[3][];

        static void Main(string[] args) {
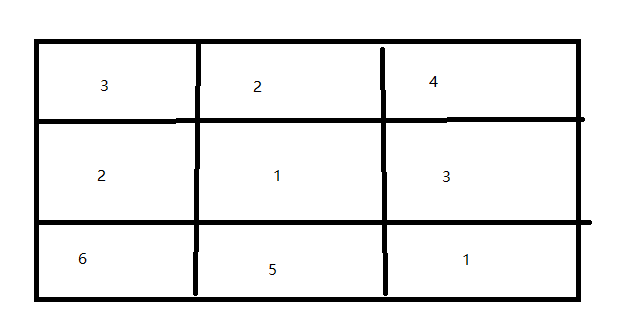
            apple[0] = new int[] {3,2,4};
            apple[1] = new int[] { 2,1,3 };
            apple[2] = new int[] { 6,5,1};
            appleSum[0] = new int[apple[0].Length];
            appleSum[1] = new int[apple[0].Length];
            appleSum[2] = new int[apple[0].Length];

            appleSum[0][0] = apple[0][0];//初始只能取到本身
            //先填充第一行与第一列
            for (int i = 1; i < apple.Length; i++)
            {
                appleSum[0][i] = appleSum[0][i - 1] + apple[0][i];
                appleSum[i][0] = appleSum[i-1][0] + apple[i][0];

            }
            //当前位置记为array[x][y] 然后填充其他行与列 值为max(array[x+1][y],array[x][y+1])
            for (int x = 1; x < apple.Length; x++)
                for (int y = 1; y < apple[0].Length; y++)
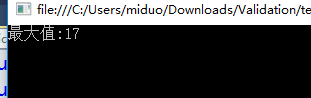
                    appleSum[x][y]= (appleSum[x - 1][y] > appleSum[x][y - 1] ? appleSum[x - 1][y] : appleSum[x][y - 1])+apple[x][y];

            Console.WriteLine("最大值:"+appleSum[apple.Length-1][apple[0].Length-1]);

            Console.Read();
        }

    }

}

　　

　　

具体分析  http://www.cnblogs.com/lihonglin2016/p/4298432.html