DEFENSE-GAN: PROTECTING CLASSIFIERS AGAINST ADVERSARIAL ATTACKS USING GENERATIVE MODELS

目录

• 概
• 主要内容

Samangouei P, Kabkab M, Chellappa R, et al. Defense-GAN: Protecting Classifiers Against Adversarial Attacks Using Generative Models.[J]. arXiv: Computer Vision and Pattern Recognition, 2018.

@article{samangouei2018defense-gan:,

title={Defense-GAN: Protecting Classifiers Against Adversarial Attacks Using Generative Models.},

author={Samangouei, Pouya and Kabkab, Maya and Chellappa, Rama},

journal={arXiv: Computer Vision and Pattern Recognition},

year={2018}}

概

本文介绍了一种针对对抗样本的defense方法, 主要是利用GAN训练的生成器, 将样本\(x\)投影到干净数据集上\(\hat{x}\).

主要内容

我们知道, GAN的损失函数到达最优时, \(p_{data}=p_G\), 又倘若对抗样本的分布是脱离于\(p_{data}\)的, 则如果我们能将\(x\)投影到真实数据的分布\(p_{data}\)(如果最优也就是\(p_G\)), 则我们不就能找到一个防御方法了吗?

对于每一个样本, 首先初始化\(R\)个随机种子\(z_0^{(1)}, \ldots, z_0^{(R)}\), 对每一个种子, 利用梯度下降(\(L\)步)以求最小化

\[\tag{DGAN}
\min \quad \|G(z)-x\|_2^2,
\]

其中\(G(z)\)为利用训练样本训练的生成器.

得到\(R\)个点\(z_*^{(1)},\ldots, z_*^{(R)}\), 设使得(DGAN)最小的为\(z^*\), 以及\(\hat{x} = G(z^*)\), 则\(\hat{x}\)就是我们要的, 样本\(x\)在普通样本数据中的投影. 将\(\hat{x}\)喂入网络, 判断其类别.

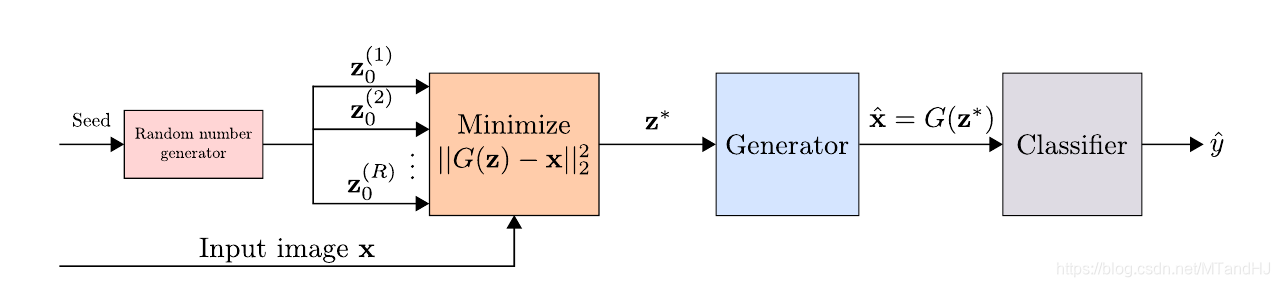
另外, 作者还在实验中说明, 可以直接用\(\|G(z^*)-x\|_2^2 \frac{<}{>} \theta\) 来判断是否是对抗样本, 并计算AUC指标, 结果不错.

注: 这个方法, 利用梯度方法更新的难处在于, \(x \rightarrow \hat{x}\)这一过程, 包含了\(L\)步的内循环, 如果直接反向传梯度会造成梯度爆炸或者消失.