Scalable Rule-Based Representation Learning for Interpretable Classification

目录

• 概
• 主要内容

Wang Z., Zhang W., Liu N. and Wang J. Scalable rule-based representation learning for interpretable classification. In Advances in Neural Information Processing Systems (NIPS), 2021.

概

传统的诸如决策树之类的机器学习方法具有很强的结构性, 也因此具有很好的可解释性. 和深度学习方法相比, 这类方法比较难以推广到大规模的问题上, 很重要的一个原因便是, 其离散的参数和结构导致无法利用梯度进行优化. 本文是对利用梯度来优化这些模型的一个尝试.

主要内容

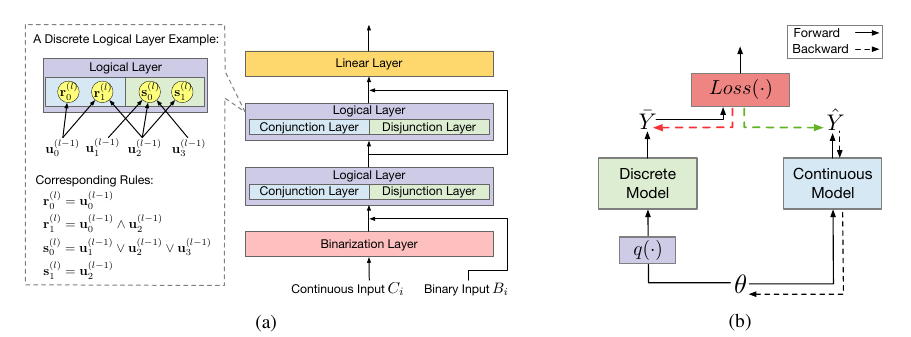
本文考虑的是上图(a)中的离散模型, 其接受连续变量\(C_i\)和离散变量\(B_i\):

1. 通过Binarization Layer 将连续变量\(C_i\)离散化并与\(B_i\)拼接得到输入\(\bm{u}^{(0)}\);
2. 对于Logical Layer, 其以\(\bm{u}^{l-1}\)为输入, 输出\(\bm{u}^l\), 其包含且\(\bm{r}\)和或\(\bm{s}\)两个部分:

\[r_i^{(l)} = \bigwedge_{W_{ij}^{(l, 0)} = 1} u_j^{(l-1)}, \\
s_i^{(l)} = \bigvee_{W_{ij}^{(l, 1)} = 1} u_j^{(l-1)}. \\
\]

其中\(W^{(l, 0)}\)表示\(\bm{r}\)与\(\bm{u}\)的邻接矩阵, 而\(W^{(l, 1)}\)表示\(\bm{s}\)与\(\bm{u}\)的邻接矩阵. 可以发现, Logical Layer中的输入输出和权重都是二元的.

3. 最后通过一个线性层进行分类, 需要说明的是, 线性层的权重是连续的.

显然由于logical layer是离散的, 直接通过梯度更新是办不到的. 一个自然的想法是用一个连续的版本\(\hat{\mathcal{F}}(X; \theta)\)进行替换, 更新连续的参数\(\theta\)然后获得下列的离散的版本:

\[\mathcal{F}(X; q(\theta)), \quad q(x) = \mathbb{I}_{x > 0.5}.
\]

显然直接套用这个方法是低效的, 因为训练过程和离散没有任何关系, 我们没法保证离散后的模型依旧是有效的, 此外还有一个问题, 上述离散模型如何匹配到一个连续的版本.

下面是一个有趣的解决方案, 假设\(\hat{W}_{i,j} \in [0, 1]\), 则

\[Conj (\bm{u}, W_i) = \prod_{j=1}^n \bigg\{1 - W_{i,j}(1 - u_j) \bigg\}, \\
Disj (\bm{u}, W_i) = 1 - \prod_{j=1}^n \bigg\{1 - W_{i,j}u_j \bigg\}, \\
\]

便为且和或操作的连续版本.

试想:

\[\begin{array}{ll}
& r_i = 1 \\
\Leftrightarrow & \bigwedge_j [u_j^{(l-1)} \vee (1 - W_{ij})] = 1\\
\Leftrightarrow & \prod_j \bigg\{1 - W_{i,j}(1 - u_j) \bigg\} = 1.\\
\end{array}
\]

其它情况可以类似推导, 实在是有趣.

但是上述式子在实际中会有一些梯度消失的问题(因为连乘号, 且内部是[0, 1]之间的), 所示在实际使用中, 作者加了一个投影算子

\[Conj_+ = \mathbb{P}(Conj (\bm{u}, W_i)),
\]

其中(这设计都是为了避免梯度消失, 怎么想到的? 怎么会往这个方向去想的?)

\[\mathbb{P}(v) = \frac{-1}{-1 + \log (v)}.
\]

解决了连续版本的问题, 现在剩下的难啃的地方是如何更新\(\theta\)以保证\(q(\theta)\)也是有意义的.

作者采用如下的梯度更新公式:

\[\theta^{t+1} = \theta^t - \eta \frac{\partial \mathcal{L}(\bar{Y})}{\partial \bar{Y}} \cdot \frac{\partial \hat{Y}}{\partial \theta^t},
\]

其中\(\hat{Y} = \hat{\mathcal{F}}(X; \theta)\), \(\bar{Y} = \mathcal{F}(X; \bar{\theta})\).

作者用了一个嫁接的例子来说明该思想, 即损失关于预测的导数用离散的, 内部的导数用连续的.

我惊讶的是, 这些改动居然work? 太不可思议了.