探索颜色渐变绘制算法(基于Processing语言) 第一部分

突然间意识到连续变化的颜色在程序中是如何实现的这一问题。没错，就想有事找事，我会分好几部分慢慢探寻，其实笔者也不会，咱一起研究。ok,我们开始！

第一部分

初始部分就从官方案例来入手学习。官方给了三个相似问题的解决方案：

其中LinearGradient是线性渐变，即两点渐变，RadialGradient是基于圆心渐变，WaveGradient是基于sin函数来绘制渐变色。我们从第一个入手，从两点开始【拉渐变】。

开始

官方示例很明确是采用绘制多条Line来达成效果，即每根线都紧挨着，在宏观上看呈现连续的色块，即：

/**
 * Simple Linear Gradient
 *
 * The lerpColor() function is useful for interpolating
 * between two colors.
 */
// Constants
int Y_AXIS = 1;
int X_AXIS = 2;		//设立横纵两轴拉渐变的方法
color b1, b2, c1, c2;
void setup() {
  size(640, 360);
  // Define colors
  b1 = color(255);
  b2 = color(0);
  c1 = color(204, 102, 0);
  c2 = color(0, 102, 153);
  noLoop();
}
void draw() {
  // Background
  setGradient(0, 0, width/2, height, b1, b2, X_AXIS);
  setGradient(width/2, 0, width/2, height, b2, b1, X_AXIS);
  // Foreground
  setGradient(50, 90, 540, 80, c1, c2, Y_AXIS);
  setGradient(50, 190, 540, 80, c2, c1, X_AXIS);
}
void setGradient(int x, int y, float w, float h, color c1, color c2, int axis ) {
  noFill();
  if (axis == Y_AXIS) {  // Top to bottom gradient
    for (int i = y; i <= y+h; i++) {
      float inter = map(i, y, y+h, 0, 1);
      color c = lerpColor(c1, c2, inter);
      stroke(c);
      line(x, i, x+w, i);
    }
  }
  else if (axis == X_AXIS) {  // Left to right gradient
    for (int i = x; i <= x+w; i++) {
      float inter = map(i, x, x+w, 0, 1);
      color c = lerpColor(c1, c2, inter);   //取两色之间的差值
      stroke(c);        			//每次划线都采取相邻的颜色值
      line(i, y, i, y+h);			//绘制连续的直线
    }
  }
}

代码中设定了横纵两轴方向性，然后新建了自己的函数setGradient()。参数有起始位置以及宽高数值，还有两个颜色极值参考，使用lerpColor()算出介于两颜色间的中间值并定义划线颜色，然后统一在for循环中画出：

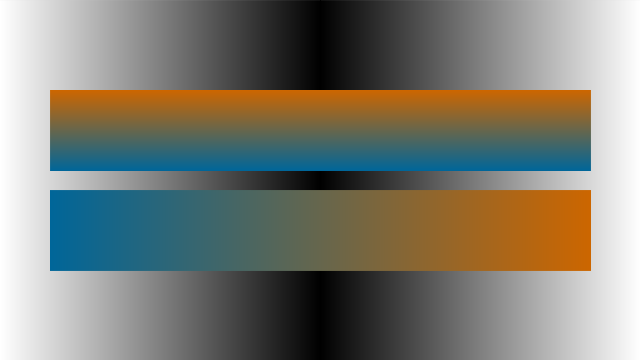
那么我们可以借它的思想来修改。setGradient()重新编写：

void setGradient(int x, int y, float w, float h, color c1, color c2) {   //方向性选择去掉
  noFill();
  for (int i = y; i <= y+h; i++) {
    float inter = map(i, y, y+h, 0, 1);
    color c = lerpColor(c1, c2, inter);
    stroke(c);
    line(x, i, x+w, i);
  }
}

然后可以用该方法绘制出特定方向[横纵两方向]的渐变色，并且可以实时绘制。如：

setGradient(50, 0, width, mouseY, c1, c2);

接着

如果想不定方向地绘制渐变呢？现在的思路是，随意的拖拽鼠标，记录两点，一点为起始点击位置，一点为终点拖拽位置，基于这两点的长度和方向来绘制line线，其中线的颜色基于两个颜色值进行lerpColor()计算得来。先上代码：

PVector p1;
PVector p2;
PVector p3;
PVector p4;
PVector p5, p6;
float len;
color  c1, c2;
int index = 0;
boolean showUI = true;
void setup()
{
  size(800, 600);
  //fullScreen();
  c1 = color(204, 102, 0);
  c2 = color(0, 102, 153);
}
void draw()
{
  background(0);
  //setGradient(50, 0, width, mouseY, c1, c2);
  if (showUI)
  {
    push();
    noFill();
    stroke(250);
    if (p1 != null)
      circle(p1.x, p1.y, 30);
    if (p2 != null)
      circle(p2.x, p2.y, 30);
    if (p2 != null && p1 != null)
    {
      line(p2.x, p2.y, p1.x, p1.y);
      p3 = PVector.sub(p2, p1).normalize().rotate(HALF_PI);
      p3.mult(60).add(p1);
      p4 = PVector.sub(p2, p1).normalize().rotate(-HALF_PI);
      p4.mult(60).add(p1);
      line(p4.x, p4.y, p3.x, p3.y);
      p5 = PVector.sub(p2, p1).normalize().rotate(HALF_PI);
      p5.mult(60).add(p2);
      p6 = PVector.sub(p2, p1).normalize().rotate(-HALF_PI);
      p6.mult(60).add(p2);
      line(p6.x, p6.y, p5.x, p5.y);
      len = PVector.sub(p1,p2).mag();
      for (float i = 0; i <= len; i+=1.0) {
        float x = lerp(p3.x, p5.x, i/len);   //使用lerp函数求得两点之间的中间差值点位置，下同
        float y = lerp(p3.y, p5.y, i/len);
        point(x, y);
        float x2 = lerp(p4.x, p6.x, i/len);
        float y2 = lerp(p4.y, p6.y, i/len);
        point(x2, y2);
          float inter = map(i, 0, len, 0.0, 1.0);
          color c = lerpColor(c1, c2, inter);
          stroke(c);
          line(x, y, x2, y2);
      }
    }
    pop();
  }
}
void setGradient(int x, int y, float w, float h, color c1, color c2) {
  noFill();
  for (int i = y; i <= y+h; i++) {
    float inter = map(i, y, y+h, 0, 1);
    color c = lerpColor(c1, c2, inter);
    stroke(c);
    line(x, i, x+w, i);
  }
}
void mousePressed() {
    p1 = null;    //复位
    p2 = null;
    p1 = new PVector(mouseX, mouseY);
}
void mouseDragged(){
    p2 = new PVector(mouseX, mouseY);      //实时更新第二个点位置
}
void mouseReleased(){
    //p2 = new PVector(mouseX, mouseY);
    println(len);    //将两点距离打印出来
}
void keyPressed() {
  showUI = !showUI;
}

其中鼠标的操作通过mousePressed() mouseDragged() mouseReleased()等事件达成。至于渐变方块的方向计算，具体大小确定，都基于基本的矢量运算得来，详情请参考源代码。效果如下：

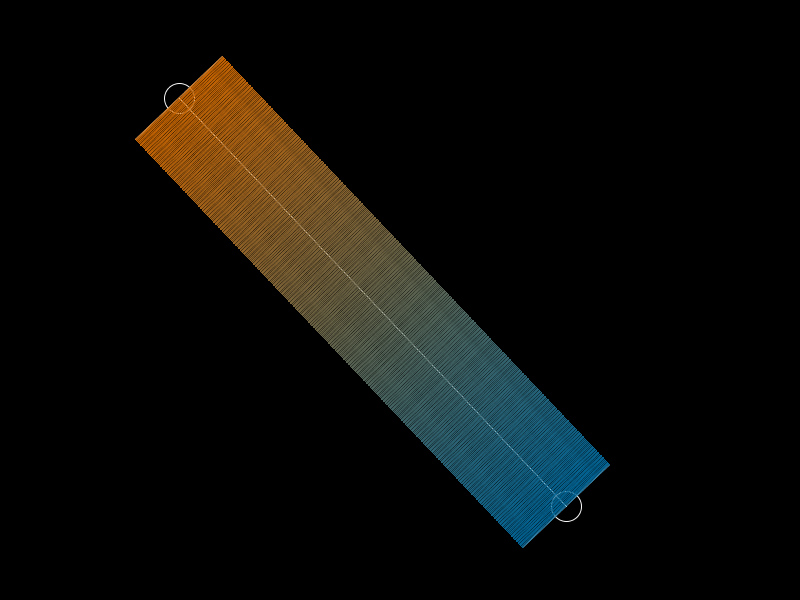
说一下不足。很明显，这样拉出来的渐变带有空隙，不能完美的填充所有像素点，和理想状态差很多，但至少已经达成了初步的想法，在Processing中【拉渐变】！

改进

我们能不能沿用这个思路来改进一下？借用讨巧的方法---矩阵变换。我们先拉出横平竖直的渐变，然后旋转它，最后呈现出来。在P5中默认是画在了一个PGraphics g的图层上，所以渐变让其绘制在单独的一层上方便旋转等变换操作，修改上文代码：

PVector p1;
PVector p2;
PVector p3;
PVector p4;
PVector p5, p6;
PGraphics pg;
float len;
color  c1, c2;
int index = 0;
boolean showUI = true;
void setup()
{
  size(800, 600);
  //fullScreen();
  c1 = color(204, 102, 0);
  c2 = color(0, 102, 153);
  float pgsize = sqrt(sq(width)+sq(height));
  pg = createGraphics(120, (int)pgsize);
}
void draw()
{
  background(0);
  if (showUI)
  {
    push();
    noFill();
    stroke(250);
    if (p1 != null)
      circle(p1.x, p1.y, 30);
    if (p2 != null)
      circle(p2.x, p2.y, 30);
    if (p2 != null && p1 != null)
    {
      line(p2.x, p2.y, p1.x, p1.y);
      p3 = PVector.sub(p2, p1).normalize().rotate(HALF_PI);
      p3.mult(60).add(p1);
      p4 = PVector.sub(p2, p1).normalize().rotate(-HALF_PI);
      p4.mult(60).add(p1);
      line(p4.x, p4.y, p3.x, p3.y);
      p5 = PVector.sub(p2, p1).normalize().rotate(HALF_PI);
      p5.mult(60).add(p2);
      p6 = PVector.sub(p2, p1).normalize().rotate(-HALF_PI);
      p6.mult(60).add(p2);
      line(p6.x, p6.y, p5.x, p5.y);
      len = PVector.sub(p1, p2).mag();
      setGradient(0,0, 60+60, len, c1, c2);   //在新图层上绘制渐变   注意这里宽度设为120，默认基于原点开始画
      push();
      translate(p3.x, p3.y);
      rotate(PVector.sub(p2, p1).heading()-HALF_PI);  //作旋转矩阵变换
      push();
      //translate(-p3.x, -p3.y);
      image(pg, 0, 0);   //渲染新图层
      pop();
      pop();
    }
    pop();
  }
}
void setGradient(float x, float y, float w, float h, color c1, color c2) {
  pg.beginDraw();
  pg.background(0, 0);
  pg.noFill();
  for (float i = y; i <= y+h; i++) {
    float inter = map(i, y, y+h, 0, 1.0);
    color c = lerpColor(c1, c2, inter);
    pg.stroke(c);
    pg.line(x, i, x+w, i);
  }
  pg.endDraw();
}
void mousePressed() {
  p1 = null;
  p2 = null;
  p1 = new PVector(mouseX, mouseY);
}
void mouseDragged() {
  p2 = new PVector(mouseX, mouseY);
}
void mouseReleased() {
  //p2 = new PVector(mouseX, mouseY);
  println(len);
}
void keyPressed() {
  showUI = !showUI;
}

新建PGraphics pg,然后绘制函数改成：

void setGradient(float x, float y, float w, float h, color c1, color c2) {
  pg.beginDraw();
  pg.background(0, 0);
  pg.noFill();
  for (float i = y; i <= y+h; i++) {
    float inter = map(i, y, y+h, 0, 1.0);
    color c = lerpColor(c1, c2, inter);
    pg.stroke(c);
    pg.line(x, i, x+w, i);
  }
  pg.endDraw();
}

将渐变线绘制在新的图层上，这样调用rotate():

push();
  translate(p3.x, p3.y);
  rotate(PVector.sub(p2, p1).heading()-HALF_PI);
  image(pg, 0, 0);
pop();

效果如下图：

很显然，这种方法虽然讨巧，不通用，但是效果很理想，没有之前的细缝问题，而且效率很高，如果宽度调大，可以看成是全幅性的PS【拉渐变】了 ~

（下图为Processing全幅两点渐变效果以及P5制作环境）

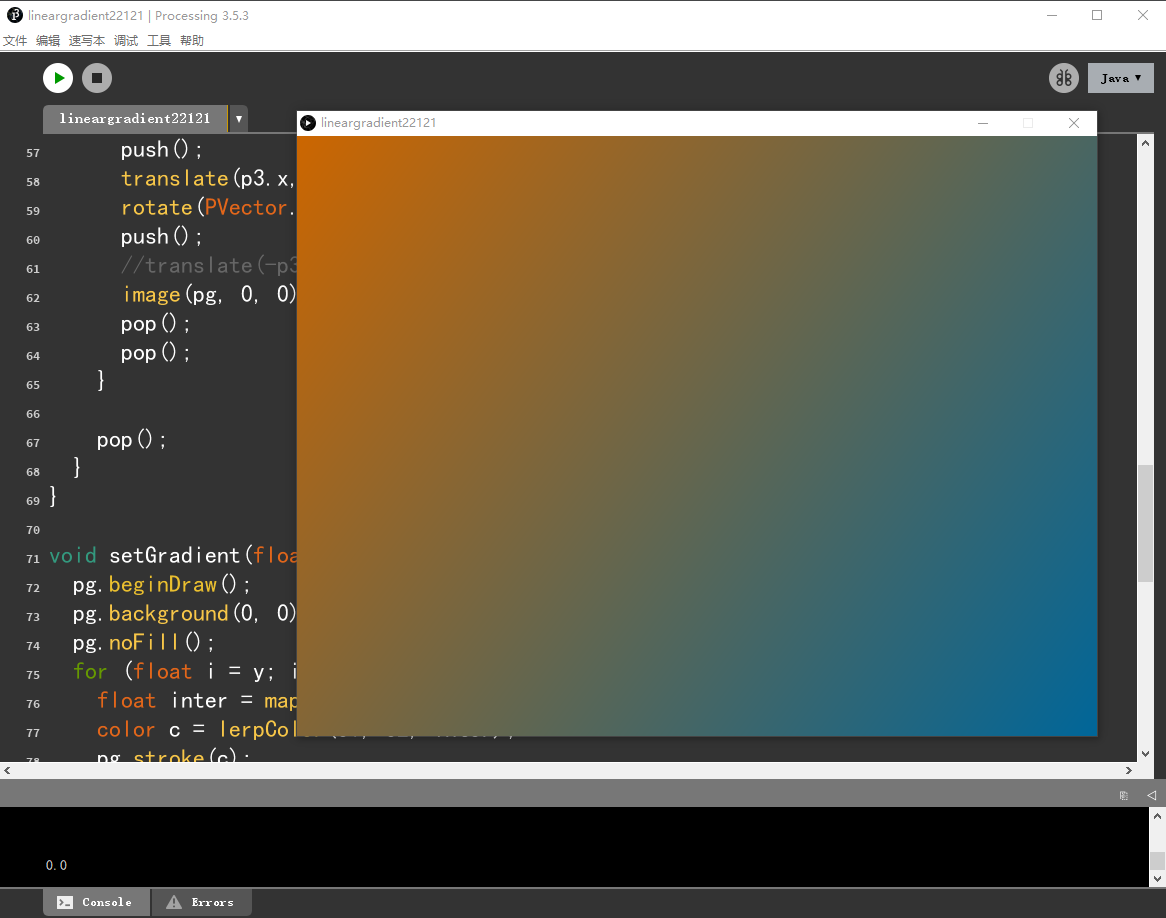
尾声

最初的预想效果正是两点线性渐变，那么接下来要在此基础上进行拓展，比如可视化取点，像ps中的编辑器一样，其次渐变风格可以切换，如圆型渐变、菱形渐变等，再次是非线性渐变算法等，好吧，是有难度的，慢慢来吧 ~ 希望可以借这篇文章给读者一些参考和借鉴，感谢阅读！！！