【leetcode】986. Interval List Intersections (双指针)

You are given two lists of closed intervals, firstList and secondList, where firstList[i] = [starti, endi] and secondList[j] = [startj, endj]. Each list of intervals is pairwise disjoint and in sorted order.

Return the intersection of these two interval lists.

A closed interval [a, b] (with a <= b) denotes the set of real numbers x with a <= x <= b.

The intersection of two closed intervals is a set of real numbers that are either empty or represented as a closed interval. For example, the intersection of [1, 3] and [2, 4] is [2, 3].

Example 1:

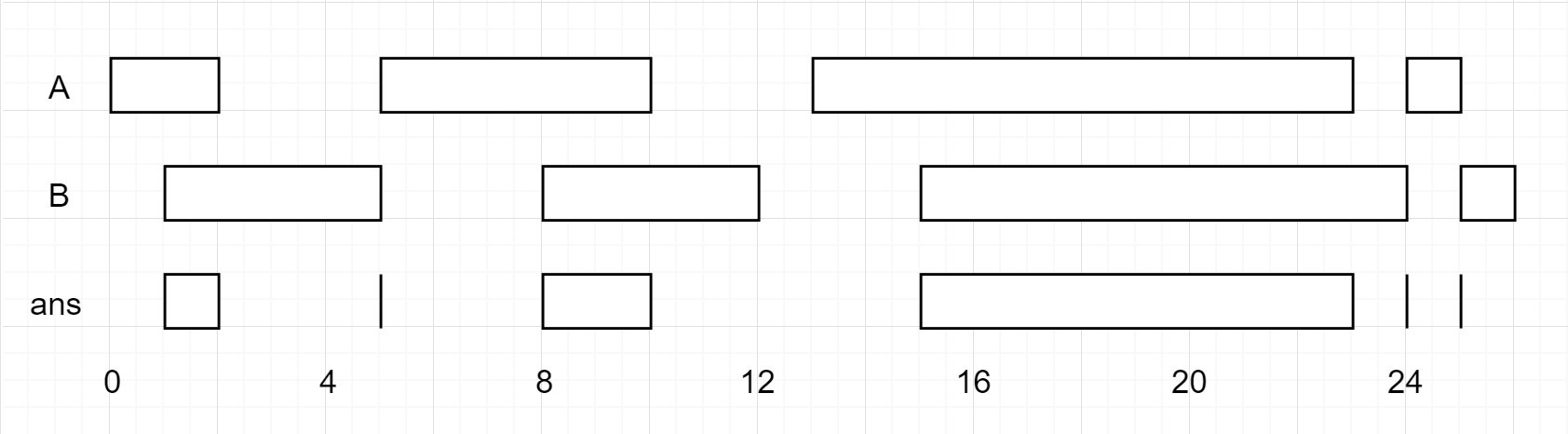
Input: firstList = [[0,2],[5,10],[13,23],[24,25]], secondList = [[1,5],[8,12],[15,24],[25,26]]
Output: [[1,2],[5,5],[8,10],[15,23],[24,24],[25,25]]

这道题需要求两个数组的公共区间的集合，如果用暴力法的话时间复杂度就是o(mn),如果用双指针的话时间复杂度就是o(m+n),这道题用双指针很有意思，需要注意的是两个指针的更新规则。

class Solution {
public:
    vector<vector<int>> intervalIntersection(vector<vector<int>>& firstList, vector<vector<int>>& secondList) {
        // 暴力法的时间复杂就是o(mn)
        // 利用双指针检索 时间复杂度为o(m+n) 用i j 分别指向firstlist 以及secondlist 中的元素
        vector<vector<int>> res;
        int m=firstList.size(),n=secondList.size();
        int i=0,j=0; //双指针
        while(i<m && j<n){
            if(firstList[i][1]<secondList[j][0]) i++;
            else if(firstList[i][0]>secondList[j][1]) j++; //没有交集 小的区间向后移动
            else{
                res.push_back({max(firstList[i][0],secondList[j][0]),min(firstList[i][1],secondList[j][1])}); //存储交集区间
                if(firstList[i][1]<secondList[j][1]) i++;
                else if (firstList[i][1]>secondList[j][1]) j++;
                else{
                    i++;
                    j++;
                }
            }
        }
        return res;

    }
};