对抗攻击(一) FGSM

引言

在对抗样本综述(二)中，我们知道了几种著名的对抗攻击和对抗防御的方法。下面具体来看下几种对抗攻击是如何工作的。这篇文章介绍FGSM(Fast Gradient Sign Method)。

预备知识

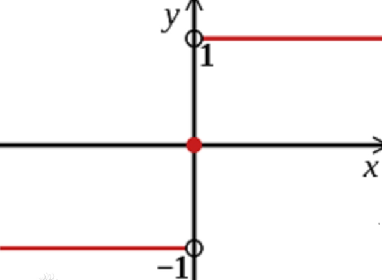
符号函数sign

泰勒展开

当函数\(f(x)\)在点\(x_0\)处可导时，在点\(x_0\)的邻域\(U(x_0)\)内恒有:

\[f(x)=f(x_0)+f'(x_0)*(x-x_0)+o(x-x_0)
\]

因为\(o(x-x_0)\)是一个无穷小量，故有:

\[f(x)≈f(x_0)+f'(x_0)*(x-x_0)
\]

这是在对函数进行局部线性化处理时常用的公式之一。从几何上看，它是用切线近似代替曲线。这样的近似是比较粗糙的，而且只在点的附近才有近似意义。

梯度

梯度是偏导数组成的向量。若有函数\(f(x^{(1)},x^{(2)},x^{(3)})\),则\(f\)在点\(θ_0=[x_0^{(1)},x_0^{(2)},x_0^{(3)}]^T\)处的梯度为：

\[\nabla f_{θ_0}=[\frac{\partial f_{θ_0}}{\partial x^{(1)}}, \frac{\partial f_{θ_0}}{\partial x^{(2)}}, \frac{\partial f_{θ_0}}{\partial x^{(3)}}]^T
\]

一元函数的导数表示函数增加最快的方向，那么梯度表示多元函数值增加最快的方向。

FGSM公式

\[\textbf{x}_{adv}=\textbf{x}+ϵ∗sign(∇_\textbf{x}J(\textbf{x},y,\textbf{θ}))
\]

ϵ为hyperparameter,控制原图像和对抗样本之间的差异程度。（字母加粗表示向量）

在梯度下降法中，我们求损失函数关于权重w、偏移b（统称参数θ）的梯度，然后更新参数，即参数\(\textbf{θ}=\textbf{θ}-η*\nabla_θ J(\textbf{x},y,\textbf{θ})\),η为learning rate。

而在FGSM中，我们用加梯度方向的ϵ倍的方式更新输入。

注意两者的不同：梯度代表函数值增加最快的方向，更新参数时，我们要做的是使损失函数J减小（在输入确定的情况下），因此减去梯度；而获取对抗样本时，我们要做的是使损失函数J增大（在θ确定的情况下），因此增加梯度，但又要控制扰动的大小，因此只取梯度的方向，其大小统一控制为ϵ。

为什么FGSM中要让损失函数增加？因为J 越大，表明预测class概率向量和真实one-hot class向量的距离越大，更有可能使预测器输出错误的label。用数学来解释下，损失函数在输入x附近\(x_{adv}\)处的泰勒展开：

\[J(\textbf{x}_{adv},y,\textbf{θ})=J(\textbf{x},y,\textbf{θ})+\nabla_x J(\textbf{x},y,\textbf{θ})^T*ϵ*sign(∇_\textbf{x}J(\textbf{x},y,\textbf{θ}))
\]

\(ϵ*sign(∇_\textbf{x}J(\textbf{x},y,\textbf{θ}))\)即泰勒展开中的\((x-x_0)\)项。

在上式中，\(\nabla_x J(\textbf{x},y,\textbf{θ})^T*ϵ*sign(∇_\textbf{x}J(\textbf{x},y,\textbf{θ}))\)为非负数，则\(J(\textbf{x}_{adv},y,\textbf{θ})>=J(\textbf{x},y,\textbf{θ})\),说明我们达到了让损失函数增大的目的。

\(\nabla_x J(\textbf{x},y,\textbf{θ})^T*ϵ*sign(∇_\textbf{x}J(\textbf{x},y,\textbf{θ}))\)是非负数，因为：

\[\nabla_x J(\textbf{x},y,\textbf{θ})^T*ϵ*sign(∇_\textbf{x}J(\textbf{x},y,\textbf{θ}))=\nabla_x J(\textbf{x},y,\textbf{θ})^T*ϵ*( ∇_\textbf{x}J(\textbf{x},y,\textbf{θ})/\Vert∇_\textbf{x}J(\textbf{x},y,\textbf{θ})\Vert)
\]

\[=ϵ*\nabla_x J(\textbf{x},y,\textbf{θ})^T*∇_\textbf{x}J(\textbf{x},y,\textbf{θ})/\Vert∇_\textbf{x}J(\textbf{x},y,\textbf{θ})\Vert
\]

\[=ϵ*\Vert∇_\textbf{x}J(\textbf{x},y,\textbf{θ})\Vert^2/\Vert∇_\textbf{x}J(\textbf{x},y,\textbf{θ})\Vert
\]

\[=ϵ*\Vert∇_\textbf{x}J(\textbf{x},y,\textbf{θ})\Vert
\]

\[>=0
\]

FGSM代码

def fgsm(model, loss, eps, softmax=False):
    """
    单次FGSM
    model为目标模型
    loss为传入的损失函数计算函数
    eps为限定扰动大小
    """
    def attack(img, label):
        output = model(img)
        if softmax:
            error = loss(output, label)
        else:
            error = loss(output, label.unsqueeze(1).float())
        error.backward()  # 计算损失函数对输入x的梯度
        # clamp()使perturbed_img的各分量在[0,1]区间
        perturbed_img = torch.clamp(img + eps * img.grad.data.sign(), 0, 1).detach()
        img.grad.zero_()
        return perturbed_img

    return attack

def ifgsm(model, loss, eps, iters=4, softmax=False):
    # 多次FGSM
    def attack(img, label):
        perturbed_img = img
        perturbed_img.requires_grad = True
        for _ in range(iters):
            output = model(perturbed_img)
            if softmax:
                error = loss(output, label)
            else:
                error = loss(output, label.unsqueeze(1).float())
            error.backward()
            temp = torch.clamp(perturbed_img + eps * perturbed_img.grad.data.sign(), 0, 1).detach()
            perturbed_img = temp.data
            perturbed_img.requires_grad = True
        return perturbed_img.detach()

    return attack

---

参考文献

[1] Goodfellow I J , Shlens J , Szegedy C . Explaining and Harnessing Adversarial Examples[J]. Computer Science, 2014.

[2] 为什么函数的导数大于等于零或小于等于零就可以判断函数是增还是减？ - Observer的回答 - 知乎 https://www.zhihu.com/question/377992767/answer/1104094160