2024.9.23 cj 训练总结

T1

这道题目仔细观察就会发现：

1. 异或
2. k=1

这就很好办，考虑 k=1 怎么解 3 1 2 4 5 6 7.......... 即可。

异或，找规律发现有很多数字的异或值为0的。最后的答案是有规律的。

不知道什么问题，场上就70分。

T2

这道题目基本上没啥思路，就是弄了个桶10分。

正解：

由于这个题目的字符集大小只有 \(26\) ,我们显然可以枚举出现次数最多与最少的字符是什么。然后把这两个字符离散出来问题就变成了只有 \(1\) 与 \(-1\) 且强制选取至少一个 \(-1\) 的最大连续子段和问题。

然后关于离散，我们显然可以用 vector 把每中字符的出现位置记录下来。然后用类似归并的方法求解即可。

关于强制选取至少一个 \(-1\) 的最大连续子段和问题,我们可以先把答案预设为 \(-1\) 然后到第一个 \(-1\) 时不减即可解决。

由于每种字符作为最大与最小总共被枚举 \(52\) 次，所有字符的数量和为 \(n\)

所以时间复杂度为 \(O(52n)\)

空间复杂度 \(O(n)\)

Code

#include<iostream>
#include<cstdio>
#include<cmath>
#include<cstring>
#include<vector>
using namespace std;

int n;
vector<int> tong[30];
char s[1000005];
int ans;

int main(){
    cin>>n>>s;
    for(int i=1;i<=n;++i){
        tong[s[i-1]-'a'].push_back(i);
    }
    for(int i=0;i<26;++i){
        if(!tong[i].size()){
            continue;
        }
        for(int j=0;j<26;++j){
            if(!tong[j].size() || i==j){
                continue;
            }
            int num1=0;int num2=0;
            bool f=0;
            int cnt=-1;
            while(num1<tong[i].size() || num2<tong[j].size()){
                int a1,a2;
                if(num1==tong[i].size()){
                    a1=1e9;
                }else{
                    a1=tong[i][num1];
                }

                if(num2==tong[j].size()){
                    a2=1e9;
                }else{
                    a2=tong[j][num2];
                }

                if(a1<a2){
                    num1++;
                    cnt++;
                }
                if(a1>a2){
                    if(f==1){
                        cnt--;
                    }
                    num2++;
                    f=1;
                }
                if(cnt<0){
                    f=0;
                    cnt=-1;
                }
                ans=max(ans,cnt);
            }
        }
    }
    cout<<ans<<'\n';
    return 0;
}

T3

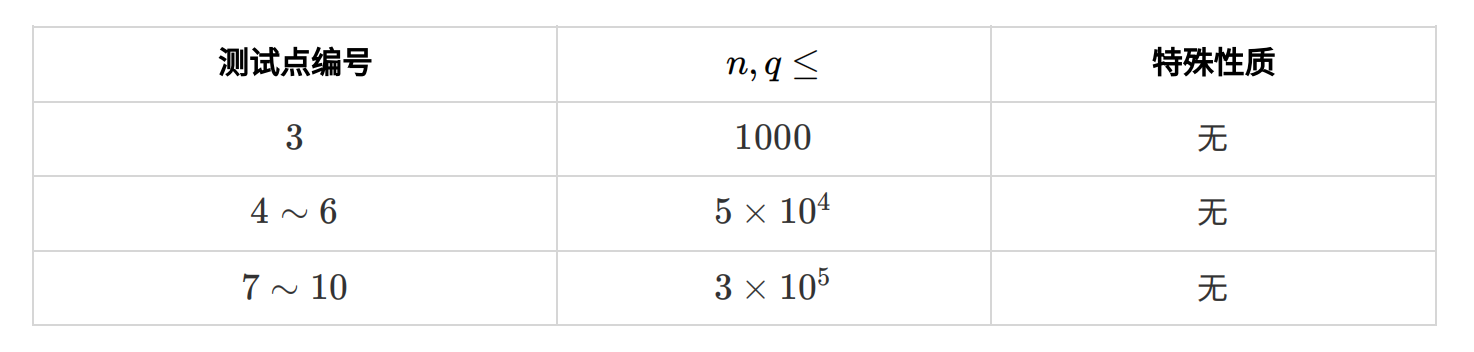
这道题目我就是对于 sub1的分就是 st表 维护一下。

对于 sub2 的分数就是纯暴力。

正解：

这道题目乍一看并没有什么思路，然后会很沮丧地发现其实两条边根本就是个乘法，根本贪心不了。

当时对这种玄学的东西一看就是 dp，然后又觉得是个斜率优化，因为有值相乘，但是dp根本设计不出来

真正的正解：

然后原题在 这里 ，但是题解并没有看懂。

单调站维护还可以，但是后面的树状数组维护真的很迷糊。

T4

完全不会。

tj：



原题