AtCoder Beginner Contest 409

A题

知识点：枚举

题意为给了两个长度为\(N\)的字符串S1和S2，字符串仅包含o和x字符，问两个字符串是否存在一个位置i使得S1[i]==S2[i]&&S1[i]=='o'。时间复杂度为\(O(n)\)。

void solve(){
	int n;cin >> n;
	string s1,s2;
	cin >> s1 >> s2;
	for(int i=0;i<n;i++){
		if(s1[i]==s2[i]&&s1[i]=='o'){
			cout << "Yes" << endl;
			return;
		}
	}
	cout << "No" << endl;
}

---

B题

知识点：枚举，排序+二分查找

题目陈述

给定一个长度为\(N\)的非负整数序列\(A = (A_1, A_2, \ldots, A_N)\)。找出满足以下条件的最大非负整数\(x\)：

• 在\(A\)中，大于或等于\(x\)的元素出现次数（包括重复元素）至少为\(x\)次。

约束条件

• \(1 \leq N \leq 100\)
• \(0 \leq A_i \leq 10^9\)
• 所有输入值均为整数。

解法：由于题目中要找大于等于\(x\)的元素个数，所以可以对序列\(A\)进行升序排序。序列最大长度不超过100，所以我们可以从0到100枚举\(x\)，看那一个符合条件即可。可以使用lower_bound()函数获得大于等于\(x\)的元素个数。时间复杂度为\(O(n\times \log{n})\)。

void solve(){
	int n;cin >> n;
	vector<int> a(n+1);
	for(int i=1;i<=n;i++){
		cin >> a[i];
	}
	sort(a.begin()+1,a.end());
	int x=0;
	for(int i=1;i<=n;i++){
		//枚举x
		int idx=lower_bound(a.begin()+1,a.end(),i)-a.begin();
		if(n-idx+1>=i) x=i;
	}
	cout << x << endl;
}

---

C题

知识点：思维，枚举

题目陈述

有一个周长为\(L\)的圆，圆上放置了点\(1, 2, \ldots, N\)。对于\(i = 1, 2, \ldots, N - 1\)，点\(i + 1\)位于点\(i\)沿顺时针方向\(d_i\)距离的位置上。

请找出满足以下两个条件的整数三元组\((a, b, c)\)（\(1 \leq a < b < c \leq N\)）的数量：

• 点\(a\)、\(b\)、\(c\)都处于不同的位置。
• 以点\(a\)、\(b\)、\(c\)为顶点的三角形是等边三角形。

约束条件

• \(3 \leq L, N \leq 3 \times 10^5\)
• \(0 \leq d_i < L\)
• 所有输入值均为整数。

解法：要出现等边三角形，肯定三个点中任意两个点之间的圆弧长度为\(\frac{L}{3}\)，点1的位置为0，每个点在圆周上的位置一定是一个整数，所以如果3不能整除\(L\)，那么一定不存在这样的等边三角形，输出为0。否则我们计算每一个点在圆周上的位置，并且用一个\(cnt\)记录每个位置点的数量，之后枚举每一个位置，计算另外两个点的位置，统计答案。这样会有一个问题就是每一个等边三角形会被重复统计，比如枚举到a点时，找到另外两个点b和c，那么枚举到b时，会找到a和c，枚举到c时，会找到a和b，那么就统计了三次，所以最后对答案除以3就是最终的答案了。时间复杂度为\(O(n)\)。

void solve(){
	int n,L;cin >> n >> L;
	vector<int> d(n);
	for(int i=1;i<n;i++) cin >> d[i];
	if(L/3*3!=L){
		cout << 0 << endl;
		return;
	}
	vector<int> loca(n+1);
	int s=0;
	loca[1]=s;
	for(int i=1;i<n;i++){
		s=(s+d[i])%L;
		loca[i+1]=s;
	}
	vector<int> cnt(L,0);
	for(int i=1;i<=n;i++){
		cnt[loca[i]]++;
	}
	int ans=0,deg=L/3;
	//枚举每一个位置
	for(int i=0;i<L;i++){
		int p=(i+deg)%L,q=(i+2*deg)%L;
		ans+=cnt[i]*cnt[p]*cnt[q];
	}
	cout << ans/3 << endl;
}

---

D题

知识点：贪心

问题陈述

给定一个长度为\(N\)、由小写英文字母组成的字符串\(S = S_1S_2\ldots S_N\)。你需要对\(S\)恰好执行一次以下操作：

• 选择\(S\)的一个长度至少为 1 的连续子串，将其循环左移 1 位。也就是说，选择整数\(1 \leq \ell \leq r \leq N\)，把\(S_\ell\)插入到\(S\)的第\(r\)个字符右侧，然后删除\(S\)的第\(\ell\)个字符。

找出执行该操作后，所有可能得到的字符串中字典序最小的那个。

你会拿到\(T\)组测试用例，请分别解决每个测试用例。

约束条件

• \(1 \leq T \leq 10^5\)
• \(1 \leq N \leq 10^5\)
• \(S\)是长度为\(N\)、由小写英文字母组成的字符串。
• \(T\)和\(N\)是整数。
• 单个输入文件中所有测试用例的\(N\)之和最多为\(10^5\)。

解法：说到字典序，我们就会想到贪心的思想。在循环左移一次后，要使得字符串字典序是操作后最小的那个，那么肯定是找到第一个\(s_i>s_{i+1}\)的位置\(l\)，循环左移后\(s_i=s_{i+1}\)。现在考虑字串的右端点\(r\)，要将\(s_l\)移动到后面某个位置，且满足在\(l+2\)到结束的某个位置\(j\)使得\(s_j>s_l\)，那么\(r=j-1\)。如果不存在大于\(s_l\)的，那么就把\(s_l\)放在最后。这样一定是最小的，也很容易证明。最后答案就是拼接就好，可以看到上面操作至少包含了3个字符，所以对于\(n \leq 2\)的情况，我们单独处理。时间复杂度为\(O(n)\)。代码写的不是太好。

void solve(){
	int n;cin >> n;
	string s;cin >> s;
	if(n<=2){
		if(n==1){
			cout << s << endl;
		}else{
			if(s[0]>s[1]){
				reverse(s.begin(),s.end());
			}
			cout << s << endl;
		}
		return;
	}
	string ans;
	bool find=false;
	for(int i=0;i<n-1;i++){
		if(s[i]>s[i+1]){
			find=true;
			//从i+2去找第一个大于当前字符的
			char c=s[i];
			ans=s.substr(0,i);
			ans+=s[i+1];
			int r=n-1,f=0;
			for(int j=i+2;j<n;j++){
				if(s[j]>c){
					r=j;
					f=1;
					break;
				}
			}
			if(f){
				for(int k=i+2;k<=r-1;k++) ans+=s[k];
				ans+=c;
				for(int k=r;k<n;k++) ans+=s[k];
			}else{
				for(int k=i+2;k<n;k++) ans+=s[k];
				ans+=c;
			}
			break;
		}
	}
	if(!find) cout << s << endl;
	else cout << ans << endl;
}

---

E题

知识点：树上dp

问题陈述

给定一棵有\(N\)个顶点的树。顶点编号为\(1, 2, \ldots, N\)，边编号为\(1, 2, \ldots, N - 1\)。边\(j\)双向连接顶点\(u_j\)和\(v_j\)，且权重为\(w_j\)。此外，顶点\(i\)被赋予一个整数\(x_i\)。如果\(x_i > 0\)，则在顶点\(i\)放置\(x_i\)个正电子；如果\(x_i < 0\)，则在顶点\(i\)放置\(-x_i\)个电子；如果\(x_i = 0\)，则顶点\(i\)不放置任何粒子。已知\(\sum_{i=1}^N x_i = 0\)。

沿边\(j\)移动一个正电子或电子需要消耗能量\(w_j\)。当正电子和电子处于同一顶点时，它们会等量相互湮灭。

请找出使所有正电子和电子湮灭所需的最小能量。

约束条件

• \(2 \leq N \leq 10^5\)
• \(|x_i| \leq 10^4\)
• \(\sum_{i=1}^N x_i = 0\)
• \(1 \leq u_j < v_j \leq N\)
• \(0 \leq w_j \leq 10^4\)
• 给定的图是一棵树。
• 所有输入值均为整数。

这道题按照给出的示例模拟一下，可以发现这个就是一道树上dp的题，所以思路也很简单了，定义\(dp[i]\)表示以\(i\)为根的子树将\(i\)的所有孩子向上移动能够获得的代价，由于正负电子相遇会抵消，所以要用一个\(cnt[i]\)来记录每一个节点的的电子情况。之后就是列状态转移方程以及初始化等问题，可以在代码中看到。时间复杂度为\(O(n)\)。

示例：

5
-2 -8 10 -2 2
3 5 1
1 3 5
2 5 0
3 4 6

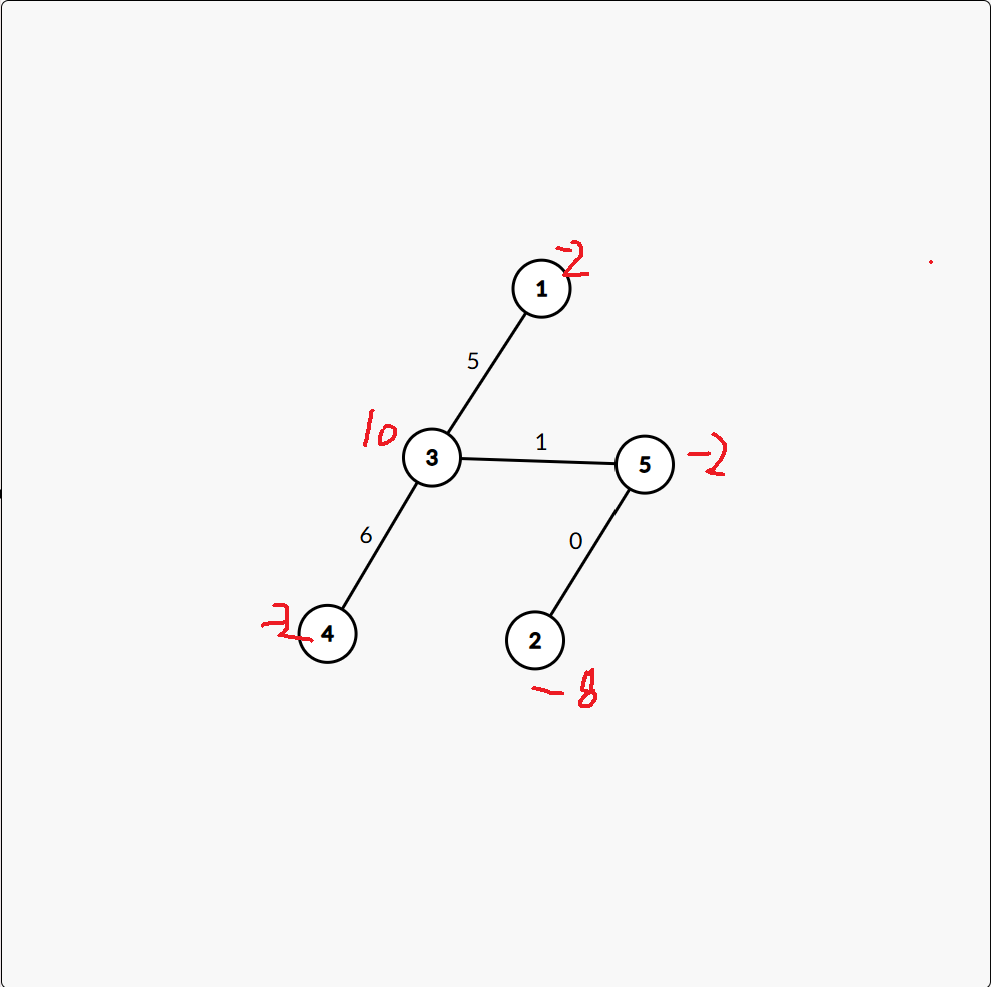
模拟一遍即可。

const int maxn=1e5+9,mod=1e9+7;
//a数组就是每个节点的电子情况，dp[i]表示以i为根的子树的花费，cnt[i]记录节点i的电子情况
int a[maxn],dp[maxn],cnt[maxn];
//tr存树
vector<pair<int,int>> tr[maxn];

void dfs(int u,int p){
    //初始化：开始每个节点为dp[u]=0,cnt[u]=a[u]
	dp[u]=0;
	cnt[u]=a[u];
	for(auto[v,w]:tr[u]){
		if(v==p) continue;
		dfs(v,u);
        //注意这里cnt[v]要加绝对值
		dp[u]+=dp[v]+w*abs(cnt[v]);
        //湮灭电子
		cnt[u]+=cnt[v];
	}
}
void solve(){
	int n;cin >> n;
	for(int i=1;i<=n;i++) cin >> a[i];
	for(int i=1;i<n;i++){
		int u,v,w;
		cin >> u >> v >> w;
		tr[u].push_back({v,w});
		tr[v].push_back({u,w});
	}
	dfs(1,0);
	cout << dp[1] << endl;
}