manim边学边做--空心多边形

空心的多边形Cutout是一种比较特殊的多边形，主要用于解决与形状、大小、位置等相关的数学问题。

Cutout多边形可以定义物体表面的空洞或凹陷部分，从而更准确地模拟现实世界中的复杂形状。

比如，在PCB（印制电路板）设计中，通过放置Cutout空心的多边形，设计师可以精确地控制铜的覆盖区域，从而优化电路布局和信号完整性。

在机械加工时，Cutout多边形也可以用于指导切割工具的运动轨迹，以便于在材料上形成精确的空洞或凹槽。

其实，在我们上学期间学习几何时，也经常遇到Cutout多边形，只是它一般不以Cutout这个名称出现。

比如，计算复杂图形的面积时，经常将其分割成几个简单的多边形（如三角形、矩形等），然后分别计算；

在证明两个图形面积相等、两线段相等或两角相等时，有时需要构造辅助线或辅助图形，这实质上也是一种“cut out”操作。

manim中虽然也可以通过组合前面几篇文章中提及的几何图形对象来构造Cutout图形，

但是直接用其manim提供的Cutout对象则更简单方便。

1. 主要参数

Cutout对象的主要参数就两个。

参数名称	类型	说明
main_shape	VMobject	被切割的主体形状
mobjects	*VMobject	从main_shape中切割出的一个或多个小形状

2. 使用示例

Cutout使用起来比较简单，下面的通用示例中展示空心多边形的使用方式，

其余几个例子演示的是Cutout在一些常见几何题目中的应用。

2.1. 通用示例

通用示例中，演示Cutout的使用方式，在一个大的四边形中切出三角形，四边形，五边形和六边形。

main = Square()scale(2)
sub1 = Triangle().scale(0.5)
sub2 = Square().scale(0.5)
sub3 = RegularPolygon(5).scale(0.5)
sub4 = RegularPolygon(6).scale(0.5)

Cutout(
    main,
    sub1,
    sub2,
    sub3,
    sub4,
    fill_opacity=1,
    color=BLUE,
    stroke_color=YELLOW,
)

2.2. 矩形中的三角形

求解矩形中的一个三角形的面积是常见的题型，利用Cutout，可以构造矩形中“切割”一个三角形的效果。

points = [A, B, C, D]
sub_points = [D, F, E]
main = Polygon(*points)
sub = Polygon(*sub_points)

Cutout(
    main,
    sub,
    fill_opacity=1,
    color=BLUE,
    stroke_color=GREEN,
)

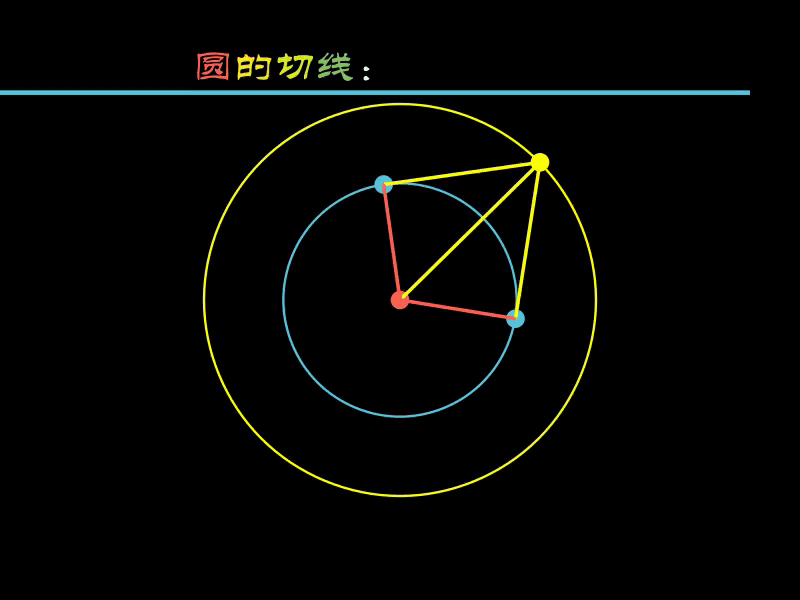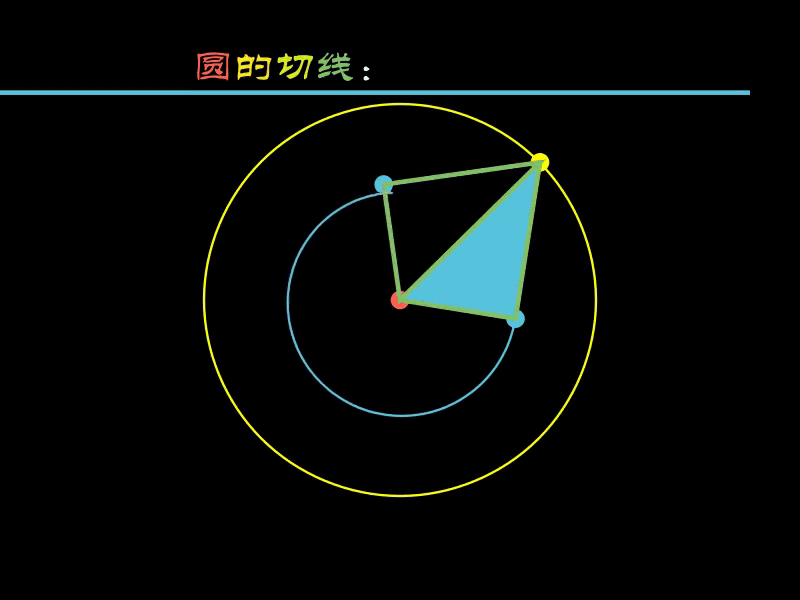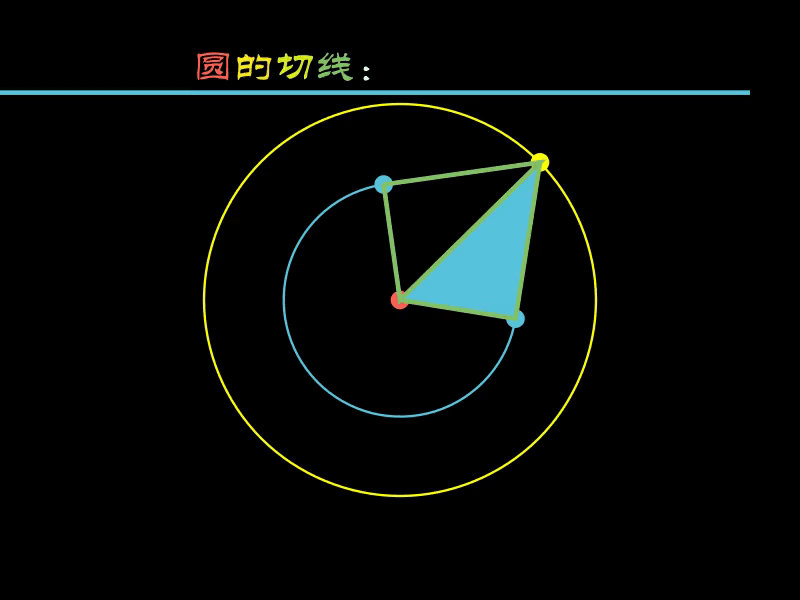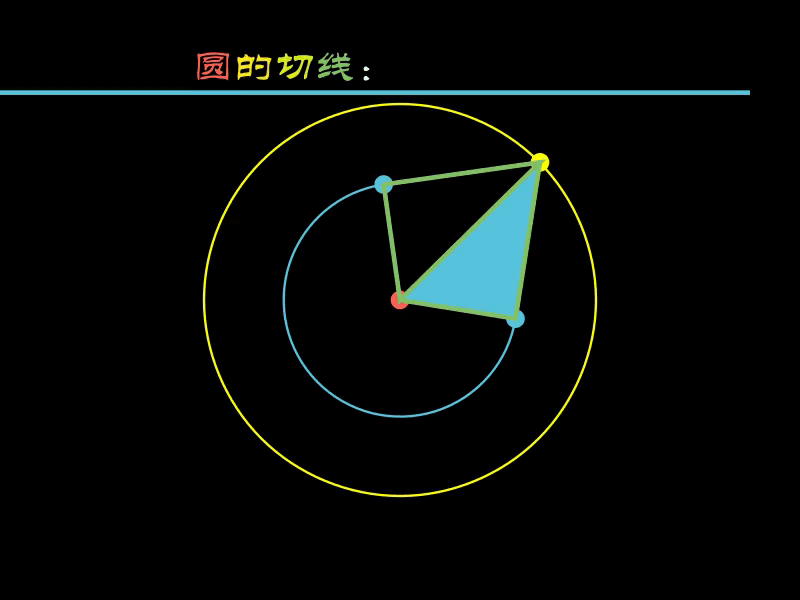
2.3. 圆的切线

圆的切线相关问题也一样，可以沿着切线进行“切割”。

下面的示例中，沿着小圆的切线切割了一个三角形。

main = Polygon(A, P, B, O)
sub = Polygon(A, P, O)
Cutout(
    main,
    sub,
    fill_opacity=1,
    color=BLUE,
    stroke_color=GREEN,
)

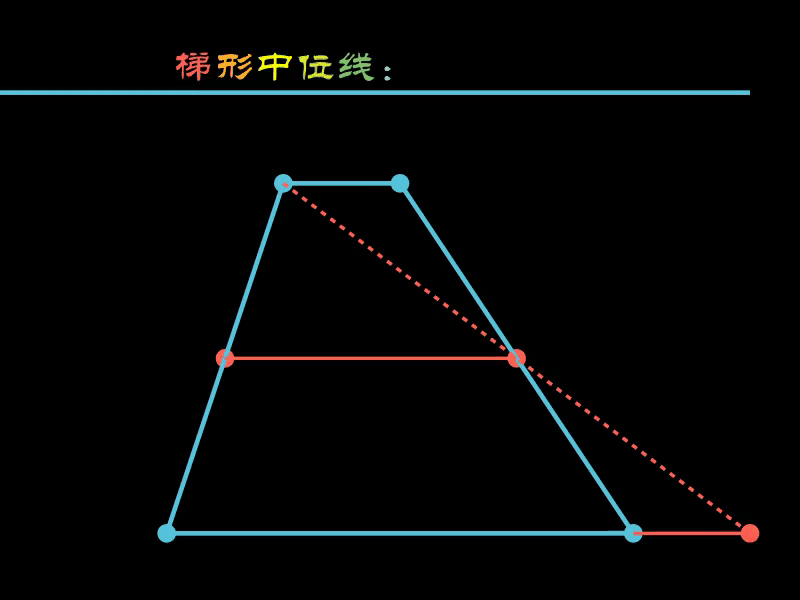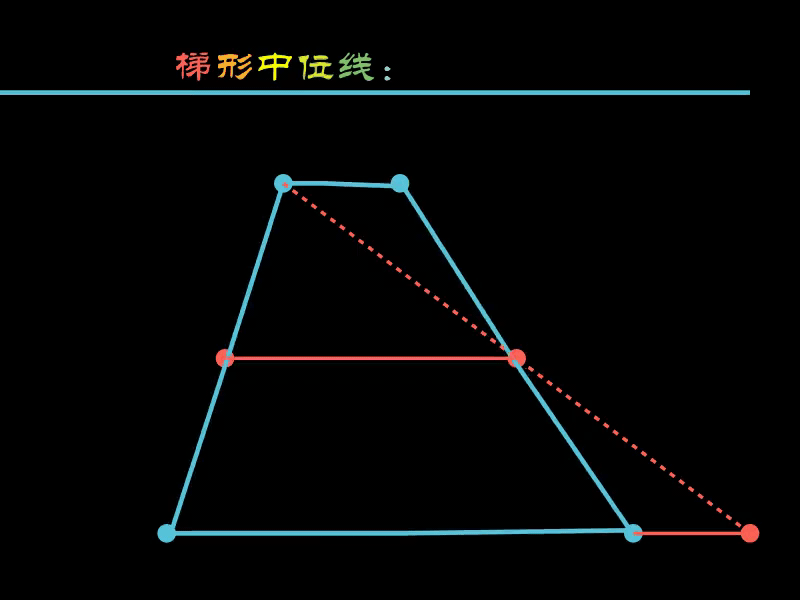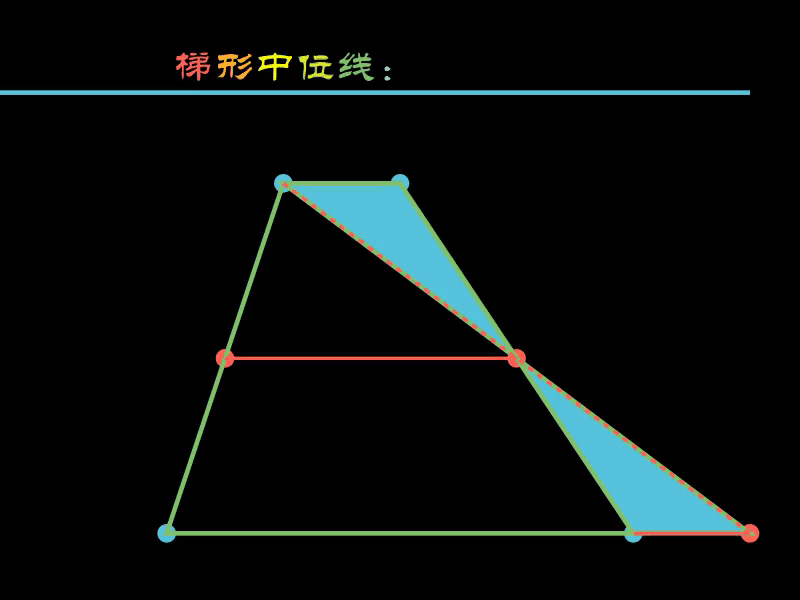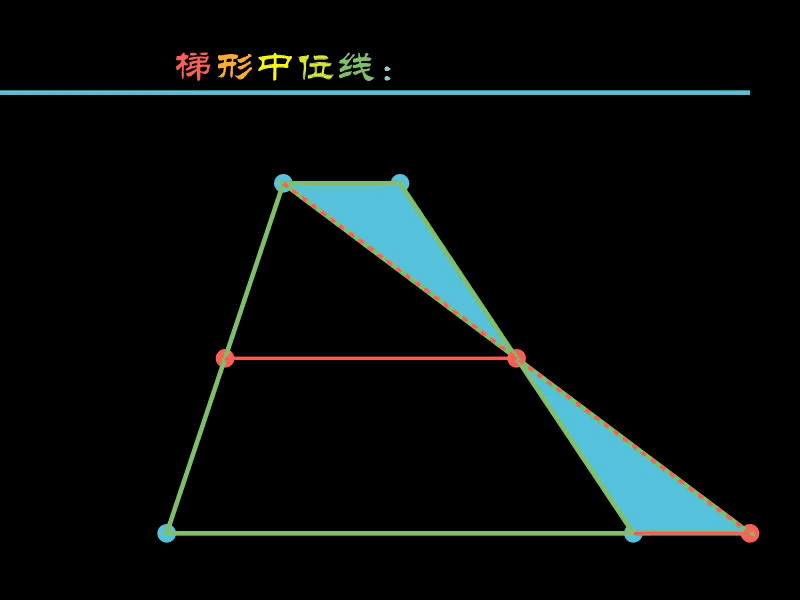
2.4. 梯形的中位线

梯形的中位线定理证明中，关键就是两个全等三角形的全等，

下面的示例将梯形的其他部分“切割”掉，只保留两个全等三角形。

main = Polygon(A, B, F, G, D)
sub = Polygon(A, F, C, D)

Cutout(
    main,
    sub,
    fill_opacity=1,
    color=BLUE,
    stroke_color=GREEN,
)

3. 附件

文中完整的代码放在网盘中了（cutout.py），

下载地址: 完整代码 (访问密码: 6872)