时间复杂度为 O(n^2) 的排序算法

对于小规模数据，我们可以选用时间复杂度为 O(n2) 的排序算法。因为时间复杂度并不代表实际代码的执行时间，它省去了低阶、系数和常数，仅代表的增长趋势，所以在小规模数据情况下， O(n2) 的排序算法可能会比 O(nlogn) 的排序算法执行效率高。不过随着数据规模增大， O(nlogn) 的排序算法是不二选择。本篇我们主要对 O(n2) 的排序算法进行介绍，在介绍之前，我们先了解一下算法特性：

• 算法特性：

  • 稳定性：经排序后，若等值元素之间的相对位置不变则为稳定排序算法，否则为不稳定排序算法

  • 原地排序：是否借助额外辅助空间

  • 自适应性: 自适应性排序受输入数据的影响，即最佳/平均/最差时间复杂度不等，而非自适应排序时间复杂度恒定

本篇我们将着重介绍插入排序，选择排序和冒泡排序了解即可。

插入排序

插入排序的工作方式像整理手中的扑克牌一样，即不断地将每一张牌插入到其他已经有序的牌中适当的位置。

插入排序的当前索引元素左侧的所有元素都是有序的：若当前索引为 i，则 [0, i - 1] 区间内的元素始终有序，这种性质被称为循环不变式，即在第一次迭代、迭代过程中和迭代结束时，这种性质始终保持不变。

不过，这些有序元素的索引位置暂时不能确定，因为它们可能需要为更小的元素腾出空间而向右移动。插入排序的代码实现如下：

    private void sort(int[] nums) {
        for (int i = 1; i < nums.length; i++) {
            int base = nums[i];

            int j = i - 1;
            while (j >= 0 && nums[j] > base) {
                nums[j + 1] = nums[j--];
            }
            nums[j + 1] = base;
        }
    }

它的实现逻辑是取未排序区间中的某个元素为基准数base，将base与其左侧已排序区间元素依次比较大小，并"插入"到正确位置。插入排序对部分有序（数组中每个元素距离它的最终位置都不远或数组中只有几个元素的位置不正确等情况）的数组排序效率很高。事实上，当逆序很少或数据量不大（n2和nlogn比较接近）时，插入排序可能比其他任何排序算法都要快，这也是一些编程语言的内置排序算法在针对小数据量数据排序时选择使用插入排序的原因。

算法特性：

• 空间复杂度：O(1)

• 原地排序

• 稳定排序

• 自适应排序：当数组为升序时，时间复杂度为 O(n)；当数组为降序时，时间复杂度为 O(n2)

希尔排序

插入排序对于大规模乱序数组排序很慢，因为它只会交换相邻的元素，所以元素只能一步步地从一端移动到另一端，如果最小的元素恰好在数组的最右端，要将它移动到正确的位置需要移动 N - 1 次。

希尔排序是基于插入排序改进的排序算法，它可以交换不相邻的元素以对数组的局部进行排序，并最终用插入排序将局部有序的数组排序。它的思想是使数组中间隔为 h 的元素有序（h 有序数组），如下图为间隔为 4 的有序数组：

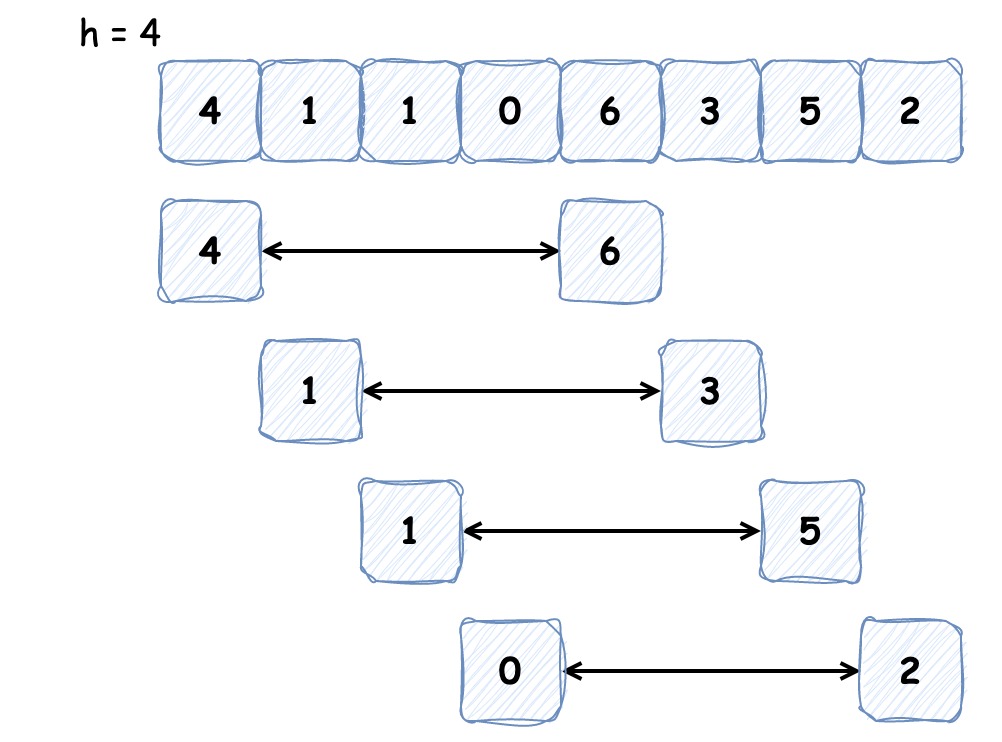
排序之初 h 较大，这样我们能将较小的元素尽可能移动到靠近左端的位置，为实现更小的 h 有序创造便利，最后一次循环时 h 为 1，便是我们熟悉的插入排序。这就是希尔排序的过程，代码实现如下：

    private void sort(int[] nums) {
        int N = nums.length;
        int h = 1;
        while (h < N / 3) {
            h = 3 * h + 1;
        }

        while (h >= 1) {
            for (int i = h; i < N; i++) {
                int base = nums[i];

                int j = i - h;
                while (j >= 0 && nums[j] > base) {
                    nums[j + h] = nums[j];
                    j -= h;
                }
                nums[j + h] = base;
            }

            h /= 3;
        }
    }

希尔排序更高效的原因是它权衡了子数组的规模和有序性，它也可以用于大型数组。排序之初，各个子数组都很短，排序之后子数组都是部分有序的，这两种情况都很适合插入排序。

---

选择排序

选择排序的实现非常简单：每次选择未排序数组中的最小值，将其放到已排序区间的末尾，代码实现如下：

    private void sort(int[] nums) {
        for (int i = 0; i < nums.length; i++) {
            int min = i;
            for (int j = i + 1; j < nums.length; j++) {
                if (nums[j] < nums[min]) {
                    min = j;
                }
            }
            swap(nums, i, min);
        }
    }

    private void swap(int[] nums, int i, int j) {
        int temp = nums[i];
        nums[i] = nums[j];
        nums[j] = temp;
    }

算法特性：

• 空间复杂度：O(1)

• 原地排序

• 非稳定排序：会改变等值元素之间的相对位置

• 非自适应排序：最好/平均/最坏时间复杂度均为 O(n2)

冒泡排序

冒泡排序通过连续地比较与交换相邻元素实现排序，每轮循环会将未被排序区间内的最大值移动到数组的最右端，这个过程就像是气泡从底部升到顶部一样，代码实现如下：

    public void sort(int[] nums) {
        for (int i = nums.length - 1; i > 0; i--) {
            // 没有发生元素交换的标志位
            boolean flag = true;
            for (int j = 0; j < i; j++) {
                if (nums[j] > nums[j + 1]) {
                    swap(nums, j, j + 1);
                    flag = false;
                }
            }

            if (flag) {
                break;
            }
        }
    }

    private void swap(int[] nums, int i, int j) {
        int temp = nums[i];
        nums[i] = nums[j];
        nums[j] = temp;
    }

算法特性：

• 空间复杂度：O(1)

• 原地排序

• 稳定排序

• 自适应排序：经过优化后最佳时间复杂度为 O(n)

---

巨人的肩膀

• 《算法导论 第三版》第 2.1 章

• 《算法 第四版》第 2.1 章

• 《Hello 算法》第 11 章

• 排序算法-希尔排序

作者：京东物流 王奕龙

来源：京东云开发者社区 自猿其说Tech 转载请注明来源