Opencv笔记（12）傅里叶变换

在之前了解的OpenCV为我们实现的图像变换，这些本质上是从图像到输出图像的映射，即输入仍是一幅图像。本章的傅里叶变换，输出数组的值在含义上和原图像的强度值大不相同，是输入图像的频域表示。

cv::dft()离散傅里叶变换

dft(InputArray src,  // 输入图像，可以是实数或虚数 
　　OutputArray dst, // 输出图像，其大小和类型取决于第三个参数flags 
　　int flags = 0,   // 转换的标识符，有默认值0
　　int nonzeroRows = 0);// 当这个参数不为0，函数会假设只有输入数组（没有设置DFT_INVERSE）的第一行或第一个输出数组（设置了DFT_INVERSE）包含非零值

flag参数

• DFT_INVERSE: 用一维或二维逆变换取代默认的正向变换
• DFT_SCALE: 缩放比例标识符，根据数据元素个数平均求出其缩放结果，如有N个元素，则输出结果以1/N缩放输出，常与DFT_INVERSE搭配使用。
• DFT_ROWS: 对输入矩阵的每一行执行正变换或逆变换；此标志允许您同时变换多个向量，并可用于减少执行3D和更高维度变换等的开销（有时比处理本身大几倍）。
• DFT_COMPLEX_OUTPUT: 对一维或二维的实数数组进行正向变换，这样的结果虽然是复数阵列，但拥有复数的共轭对称性（CCS），可以以一个和原数组尺寸大小相同的实数数组进行填充，这是最快的选择也是函数默认的方法。你可能想要得到一个全尺寸的复数数组（像简单光谱分析等等），通过设置标志位可以使函数生成一个全尺寸的复数输出数组。
• DFT_REAL_OUTPUT: 对一维二维复数数组进行逆向变换，这样的结果通常是一个尺寸相同的复数矩阵，但是如果输入矩阵有复数的共轭对称性（比如是一个带有DFT_COMPLEX_OUTPUT标识符的正变换结果），便会输出实数矩阵。

示例：

#include <opencv2/opencv.hpp>
using namespace std;
using namespace cv;
int main() {
    clock_t start, end;
    start = clock();
    int count = 0;

    Mat src = imread("F:/wallpaper/1.jpg", 0);
    //1. 放大到合适尺寸加速运算
    Mat padded;
    int opWidth = getOptimalDFTSize(src.cols);
    int opHeight = getOptimalDFTSize(src.rows);
    copyMakeBorder(src, padded, 0, opHeight - src.rows, 0, opWidth - src.cols, BORDER_REFLECT);

    //2. dft 当输入是双通道时，两个通道分别代表实部和虚部
    Mat planes[] = { Mat_<float>(padded), Mat::zeros(padded.size(),CV_32F) };
    Mat comImg;
    merge(planes, 2, comImg);
    dft(comImg, comImg, DFT_COMPLEX_OUTPUT);

    //3. 分离通道，显示幅值
    split(comImg, planes);
    Mat magMat;
    magnitude(planes[0], planes[1], magMat);
    magMat += Scalar::all(1);
    log(magMat, magMat);
    magMat = magMat(Rect(0, 0, magMat.cols & -2, magMat.rows & -2));
    normalize(magMat, magMat, 0, 1, NORM_MINMAX);

    //4. 把零频移到中心
    Mat magImg(magMat.size(), CV_8UC1);
    magMat.convertTo(magImg, CV_8UC1, 255, 0);
    magMat = magMat(Rect(0, 0, magMat.cols & -2, magMat.rows & -2));
    int cx = magImg.cols / 2;
    int cy = magImg.rows / 2;
    Mat q1 = magImg({ 0, 0, cx, cy });
    Mat q2 = magImg({ 0, cy, cx, cy });
    Mat q3 = magImg({ cx, 0, cx, cy });
    Mat q4 = magImg({ cx, cy, cx, cy });
    Mat temp;
    q1.copyTo(temp);
    q4.copyTo(q1);
    temp.copyTo(q4);
    q2.copyTo(temp);
    q3.copyTo(q2);
    temp.copyTo(q3);

    end = clock();
    cout << end - start << endl;
    return 0;
}

低频信号对应图像内变化缓慢的灰度分量。高频信号对应图像内变化越来越快的灰度分量，是由灰度的尖锐过渡造成的，例如边界。从频谱图上可以看出，当将频谱移频到原点以后，图像中心比较亮。在频谱图中，一个点的亮暗主要与这个频率中点的数目和点的灰度值有关，也就是说在空间域中包含这种频率的点越多。而经过频移后，频率为0的部分，也就是傅里叶变换所得到的常量分量在图像中心，往外扩散，点所代表的频率越来越高。也说明了图像中的“能量”主要集中在低频部分。

cv::idft()离散傅里叶逆变换

dft()不仅可以实现离散傅里叶变换，也可以实现逆变换，dft(src, dst, flags | #DFT_INVERSE) 和idft(src, dst, flags)的效果相等。

void idft(InputArray src, OutputArray dst, int flags = 0, int nonzeroRows = 0);

但是为了代码的可读性，应当使用专门的函数进行逆变换。将flag设置为DFT_REAL_OUTPUT，可以直接输入之前傅里叶变换得到的结果，得到实数矩阵的输出。

cv::mulSpectrums()频谱乘法

void mulSpectrums(InputArray a,   //输入图像（ccs or complex）
　　　　　　　　　　　　InputArray b, //和a一样为ccs格式单通道频谱or双通道复数频谱
　　　　　　　　　　　　OutputArray c, //目标数组，大小类型与输入一样                         
　　　　　　　　　　　　int flags, //只支持DFT_ROWS
　　　　　　　　　　　　bool conjB = false);//可选标志，用于决定在乘法操作前是否对第二个输入频谱取共轭。true表示取共轭；false表示不取

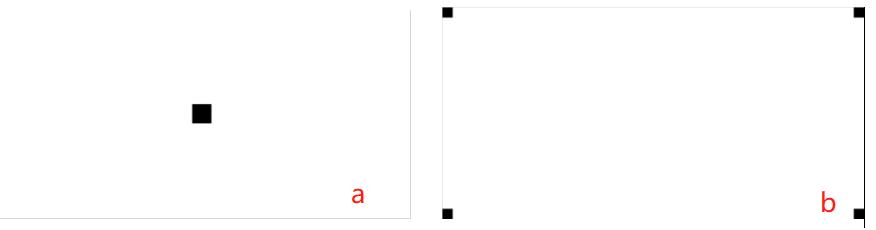
对于将零频移动到中心的频谱图，舍去中心的低频部分，只保留高频，增强图像细节，即用下图a中的mask与频谱图进行频谱乘法。如果没有移动频谱，即用下图b的mask相乘。

#include <opencv2/opencv.hpp>
using namespace std;
using namespace cv;
int main() {
    clock_t start, end;
    start = clock();
    int count = 0;

    Mat src = imread("F:/wallpaper/1.jpg", 0);
    //1. 放大到合适尺寸加速运算
    Mat padded;
    int opWidth = getOptimalDFTSize(src.cols);
    int opHeight = getOptimalDFTSize(src.rows);
    copyMakeBorder(src, padded, 0, opHeight - src.rows, 0, opWidth - src.cols, BORDER_REFLECT);

    //2. dft 当输入是双通道时，两个通道分别代表实部和虚部
    Mat planes[] = { Mat_<float>(padded), Mat::zeros(padded.size(),CV_32F) };
    Mat comImg;
    merge(planes, 2, comImg);
    dft(comImg, comImg, DFT_COMPLEX_OUTPUT);

    //3. 保留高频
    int d = 100;
    Mat mask(opHeight, opWidth, CV_8UC1, Scalar(1));
    Rect r1(0, 0, d, d);
    Rect r2(0, opHeight - d, d, d);
    Rect r3(opWidth - d, 0, d, d);
    Rect r4(opWidth-d, opHeight-d, d, d);
    mask(r1).setTo(0);
    mask(r2).setTo(0);
    mask(r3).setTo(0);
    mask(r4).setTo(0);
    mask.convertTo(mask, CV_32F);
    Mat maskImg;
    Mat masks[] = { mask,mask };
    merge(masks, 2, maskImg);
    mulSpectrums(comImg, maskImg, comImg, DFT_ROWS);

    //4. 傅里叶反变换
    Mat dst;
    idft(comImg, comImg, DFT_COMPLEX_OUTPUT);
    split(comImg, planes);
    magnitude(planes[0], planes[1], dst);
    normalize(dst, dst, 0, 1, NORM_MINMAX);
    dst.convertTo(dst, CV_8U, 255);

    end = clock();
    cout << end - start << endl;
    return 0;
}

结果：

    

参考文献：

1. 图像的二维傅里叶变换频谱图特点研究

2. OpenCV学习笔记(十)——傅里叶变换