LeetCode 周赛上分之旅 #49 再探内向基环树

️ 本文已收录到 AndroidFamily，技术和职场问题，请关注公众号 [彭旭锐] 和 BaguTree Pro 知识星球提问。

学习数据结构与算法的关键在于掌握问题背后的算法思维框架，你的思考越抽象，它能覆盖的问题域就越广，理解难度也更复杂。在这个专栏里，小彭与你分享每场 LeetCode 周赛的解题报告，一起体会上分之旅。

本文是 LeetCode 上分之旅系列的第 49 篇文章，往期回顾请移步到文章末尾~

LeetCode 周赛 365

T1. 有序三元组中的最大值 I（Easy）

• 标签：模拟、前后缀分解、线性遍历

T2. 有序三元组中的最大值 II（Medium）

• 标签：模拟、前后缀分解、线性遍历

T3. 无限数组的最短子数组（Medium）

• 标签：滑动窗口

T4. 有向图访问计数（Hard）

• 标签：内向基环树、拓扑排序、DFS

---

T1. 有序三元组中的最大值 I（Easy）

https://leetcode.cn/problems/maximum-value-of-an-ordered-triplet-i/description/

同 T2。

---

T2. 有序三元组中的最大值 II（Medium）

https://leetcode.cn/problems/maximum-value-of-an-ordered-triplet-ii/description/

问题分析

初步分析：

• 问题目标： 构造满足条件的合法方案，使得计算结果最大；
• 问题条件： 数组下标满足 $i < j < k$ 的三位数；
• 计算结果： $(nums[i] - nums[j]) * nums[k]$。

思考实现：

• T1. 有序三元组中的最大值 I 的数据量只有 $100$，枚举所有合法的 $[i, j, k]$ 组合，时间复杂度是 $O(n^3)$；
• T2. 有序三元组中的最大值 II 的数据量有 $10^5$，我们需要思考更优解法。

思考优化：

为了使得计算结果尽可能大，显然应该让乘法的左右两部分尽可能大。对于存在多个变量的问题，一个重要的技巧是 「固定一个，思考另一个」 ，这就容易多了。

• 固定 $j$： 为了让结果更大，应该找到 $nums[j]$ 左边最大的 $nums[i]$ 和右边最大的 $nums[k]$ 组合，时间复杂度是 $O(n^2)$。我们也可以使用前后缀分解预处理出来，这样时间复杂度就是 $O(n)$；
• 固定 $k$： 同理，固定 $k$ 寻找应该找到左边使得 $nums[i] - nums[j]$ 最大的方案，这可以实现线性时间和常量空间。

题解一（枚举）

枚举所有方案，记录最优解。

class Solution {
    fun maximumTripletValue(nums: IntArray): Long {
        var ret = 0L
        val n = nums.size
        for (i in 0 until n) {
            for (j in i + 1 until n) {
                for (k in j + 1 until n) {
                    ret = max(ret, 1L * (nums[i] - nums[j]) * nums[k])
                }
            }
        }
        return ret
    }
}

复杂度分析：

• 时间复杂度：$O(n^3)$
• 空间复杂度：$O(1)$

题解二（前后缀分解）

预处理出每个位置前后的最大值，再枚举 $nums[j]$ 记录最优解。

class Solution {
    fun maximumTripletValue(nums: IntArray): Long {
        val n = nums.size
        val preMax = IntArray(n)
        var sufMax = IntArray(n)
        for (i in 1 until n) {
            preMax[i] = max(preMax[i - 1], nums[i - 1])
        }
        for (i in n - 2 downTo 0) {
            sufMax[i] = max(sufMax[i + 1], nums[i + 1])
        }
        return max(0, (1 .. n - 2).maxOf { 1L * (preMax[it] - nums[it]) * sufMax[it] })
    }
}

复杂度分析：

• 时间复杂度：$O(n)$
• 空间复杂度：$O(n)$

题解三（线性遍历）

线性遍历 $nums[k]$ 并记录 $(nums[i] - nums[j])$ 的最大值，记录最优解。

class Solution {
    fun maximumTripletValue(nums: IntArray): Long {
        val n = nums.size
        var ret = 0L
        var maxDelta = 0
        var maxI = 0
        for (e in nums) {
            ret = max(ret, 1L * maxDelta * e)
            maxDelta = max(maxDelta, maxI - e)
            maxI = max(maxI, e)
        }
        return ret
    }
}

class Solution:
    def maximumTripletValue(self, nums: List[int]) -> int:
        ret = maxDelta = maxI = 0
        for e in nums:
            ret = max(ret, maxDelta * e)
            maxDelta = max(maxDelta, maxI - e)
            maxI = max(maxI, e)
        return ret

class Solution {
public:
    long long maximumTripletValue(vector<int> &nums) {
        long long ret = 0;
        int max_delta = 0, max_i = 0;
        for (int e : nums) {
            ret = max(ret, (long long) max_delta * e);
            max_delta = max(max_delta, max_i - e);
            max_i = max(max_i, e);
        }
        return ret;
    }
};

复杂度分析：

• 时间复杂度：$O(n)$
• 空间复杂度：$O(1)$

---

T3. 无限数组的最短子数组（Medium）

https://leetcode.cn/problems/minimum-size-subarray-in-infinite-array/description/

问题分析

令 $nums$ 数组的整体元素和为 $s$，考虑 $target$ 的两种情况：

• 对于 $target$ 很小的情况（小于数组整体和 $s$）：这是很简单的滑动窗口问题；
• 对于 $target$ 较大的情况（大于等于数组的整体和 $s$）：那么最小长度中一定包含整数倍的 $s$，以及某个 $nums$ 的子数组。

class Solution {
    fun minSizeSubarray(nums: IntArray, t: Int): Int {
        val n = nums.size
        val s = nums.sum()
        val k = t % s
        // 同向双指针
        var left = 0
        var sum = 0
        var len = n
        for (right in 0 until 2 * n) {
            sum += nums[right % n]
            while (sum > k) {
                sum -= nums[left % n]
                left ++
            }
            if (sum == k) len = min(len, right - left + 1)
        }
        return if (len == n) -1 else n * (t / s) + len
    }
}

复杂度分析：

• 时间复杂度：$O(n)$ 最大扫描 $2$ 倍数组长度；
• 空间复杂度：仅使用常量级别空间。

---

T4. 有向图访问计数（Hard）

https://leetcode.cn/problems/count-visited-nodes-in-a-directed-graph/description/

问题分析

初步分析：

对于 $n$ 个点 $n$ 条边的有向弱连通图，图中每个点的出度都是 $1$，因此它是一棵 「内向基环树」。那么，对于每个点有 $2$ 种情况：

• 环上节点：绕环行走一圈后就会回到当前位置，因此最长访问路径就是环长；
• 树链节点：那么从树链走到环上后也可以绕环行走一圈，因此最长访问路径就是走到环的路径 + 环长。

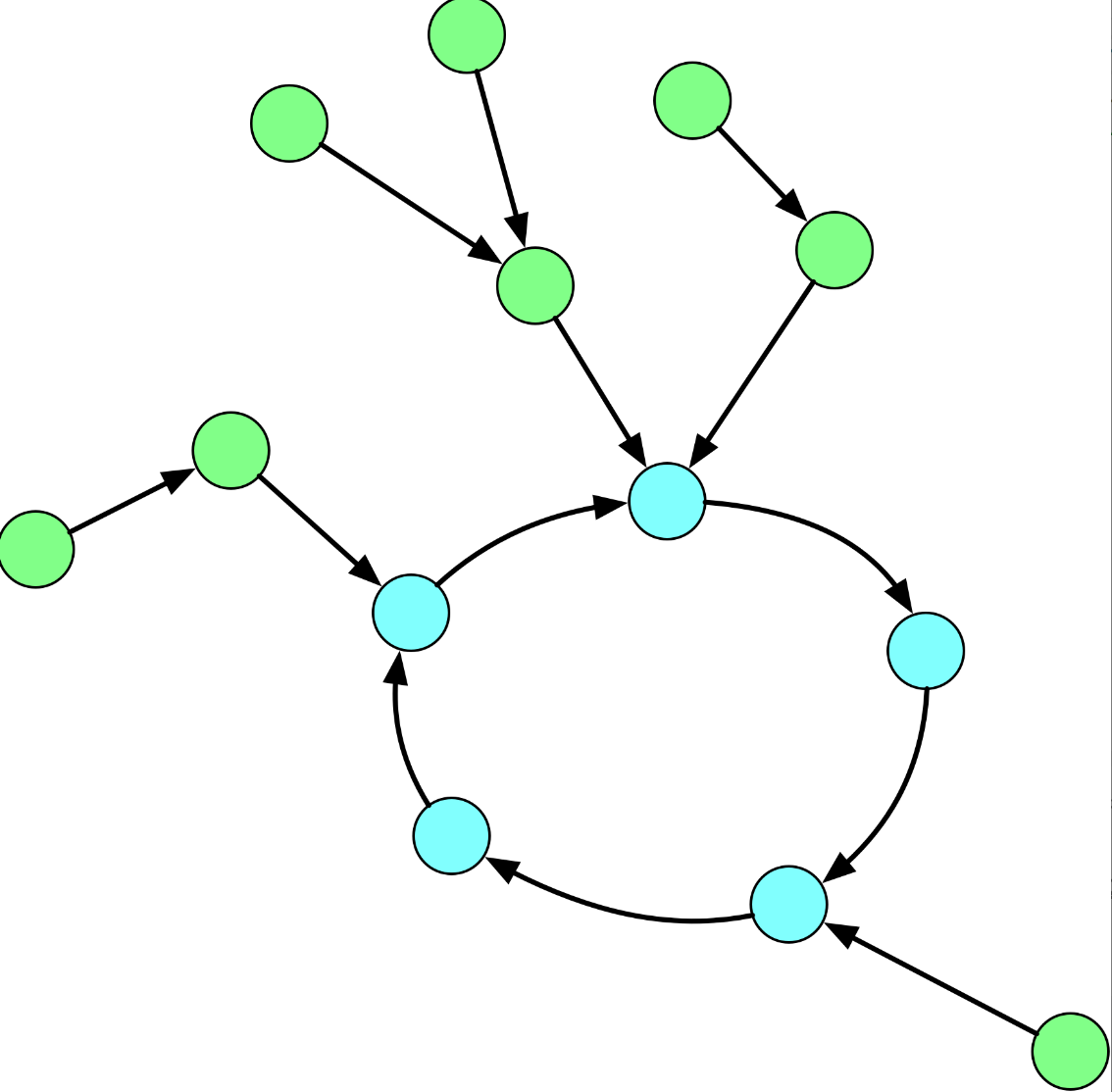
图片不记得出处了~

思考实现：

• 只有一个连通分量的情况： 那么问题就相对简单，我们用拓扑排序剪去树链，并记录链上节点的深度（到环上的距离），最后剩下的部分就是基环；
• 有多个连通分量的情况： 我们需要枚举每个连通分量的基环，再将基环的长度累加到该连通分量的每个节点。

题解（拓扑排序 + DFS）

• 第一个问题：将基环的长度累加到该连通分量的每个节点

拓扑排序减去树链很容易实现，考虑到我们这道题在找到基环后需要反向遍历树链，因此我们考虑构造反向图（外向基环树）；

• 第二个问题：找到基环长度

在拓扑排序后，树链上节点的入度都是 $0$，因此入度大于 $0$ 的节点就位于基环上。枚举未访问的基环节点走 DFS，就可以找到该连通分量的基环。

class Solution {
    fun countVisitedNodes(edges: List<Int>): IntArray {
        // 内向基环树
        val n = edges.size
        val degree = IntArray(n)
        val graph = Array(n) { LinkedList<Int>() }
        for ((x,y) in edges.withIndex()) {
            graph[y].add(x)
            degree[y]++ // 入度
        }
        // 拓扑排序
        val ret = IntArray(n)
        var queue = LinkedList<Int>()
        for (i in 0 until n) {
            if (0 == degree[i]) queue.offer(i)
        }
        while(!queue.isEmpty()) {
            val x = queue.poll()
            val y = edges[x]
            if (0 == -- degree[y]) queue.offer(y)
        }

        // 反向 DFS
        fun rdfs(i: Int, depth: Int) {
            for (to in graph[i]) {
                if (degree[to] == -1) continue
                ret[to] = depth
                rdfs(to, depth + 1)
            }
        }

        // 枚举连通分量
        for (i in 0 until n) {
            if (degree[i] <= 0) continue
            val ring = LinkedList<Int>()
            var x = i
            while (true) {
                degree[x] = -1
                ring.add(x)
                x = edges[x]
                if (x == i) break
            }
            for (e in ring) {
                ret[e] = ring.size
                rdfs(e, ring.size + 1)
            }
        }
        return ret
    }
}

复杂度分析：

• 时间复杂度：$O(n)$ 拓扑排序和 DFS 都是线性时间；
• 空间复杂度：$O(n)$ 图空间和队列空间。

题解二（朴素 DFS）

思路参考小羊的题解。

我们发现这道题的核心在于 「找到每个基环的节点」 ，除了拓扑排序剪枝外，对于内向基环树来，从任何一个节点走 DFS 走到的最后一个节点一定是基环上的节点。

在细节上，对于每个未访问过的节点走 DFS 的结果会存在 $3$ 种情况：

• 环上节点：刚好走过基环；
• 树链节点：走过树链 + 基环。
• 还有 $1$ 种情况：DFS 起点是从树链的末端走的，而前面树链的部分和基环都被走过，此时 DFS 终点就不一定是基环节点了。这种情况就同理从终点直接反向遍历就好了，等于说省略了处理基环的步骤。

class Solution {
    fun countVisitedNodes(edges: List<Int>): IntArray {
        val n = edges.size
        val ret = IntArray(n)
        val visit = BooleanArray(n)
        for (i in 0 until n) {
            if (visit[i]) continue
            // DFS
            val link = LinkedList<Int>()
            var x = i
            while (!visit[x]) {
                visit[x] = true
                link.add(x)
                x = edges[x]
            }
            if (ret[x] == 0) {
                val depth = link.size - link.indexOf(x) // (此时 x 位于基环入口)
                repeat(depth) {
                    ret[link.pollLast()] = depth
                }
            }
            var depth = ret[x]
            while (!link.isEmpty()) {
                ret[link.pollLast()] = ++depth
            }
        }
        return ret
    }
}

复杂度分析：

• 时间复杂度：$O(n)$ DFS 都是线性时间；
• 空间复杂度：$O(n)$ 图空间和队列空间。

---

推荐阅读

LeetCode 上分之旅系列往期回顾：

• LeetCode 单周赛第 364 场 · 前后缀分解结合单调栈的贡献问题
• LeetCode 单周赛第 363 场 · 经典二分答案与质因数分解
• LeetCode 双周赛第 114 场 · 一道简单的树上动态规划问题
• LeetCode 双周赛第 113 场 · 精妙的 O(lgn) 扫描算法与树上 DP 问题

️ 永远相信美好的事情即将发生，欢迎加入小彭的 Android 交流社群~