1.在原理方面

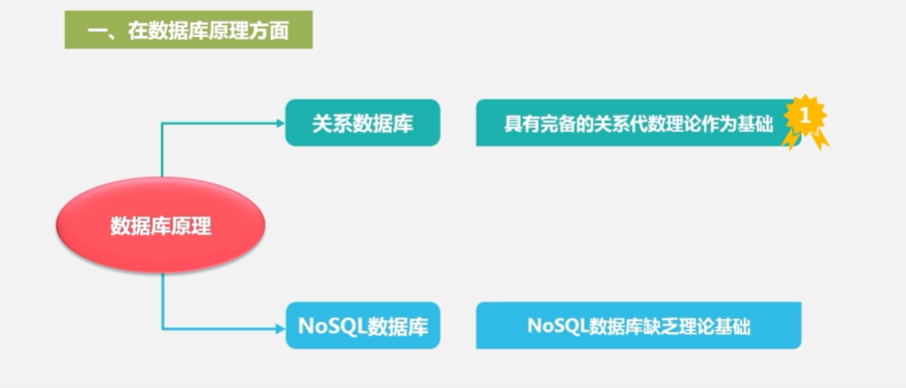
2.在数据规模方面

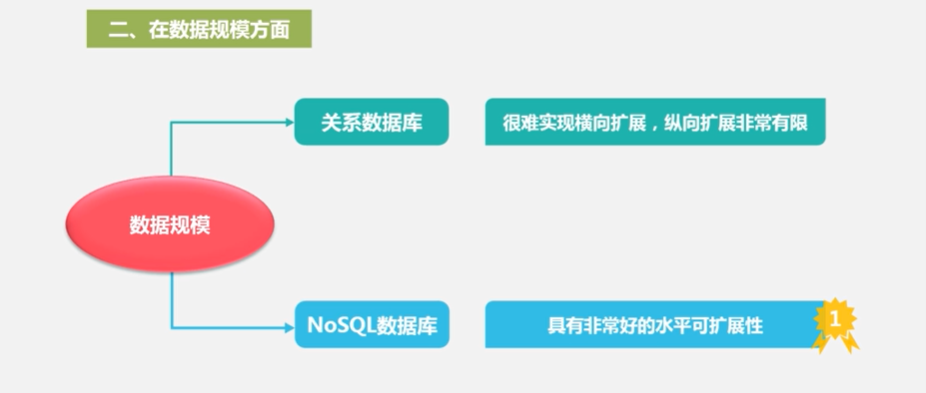
3.在数据库模式方面

4.查询效率方面：

5.在事务一致性方面：

6.在数据完整性方面：

7.在可扩展性方面：

8.在可用性方面

9.在标准化方面：

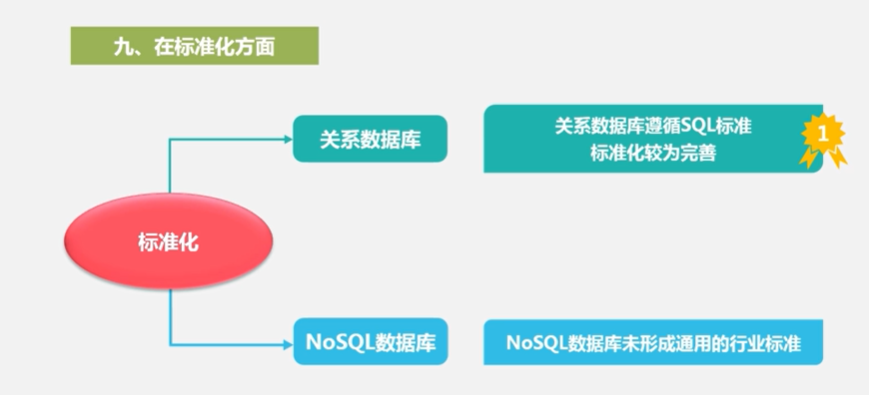
10.在技术支持方面：

11.在可维护方面：

关系数据库的优势：

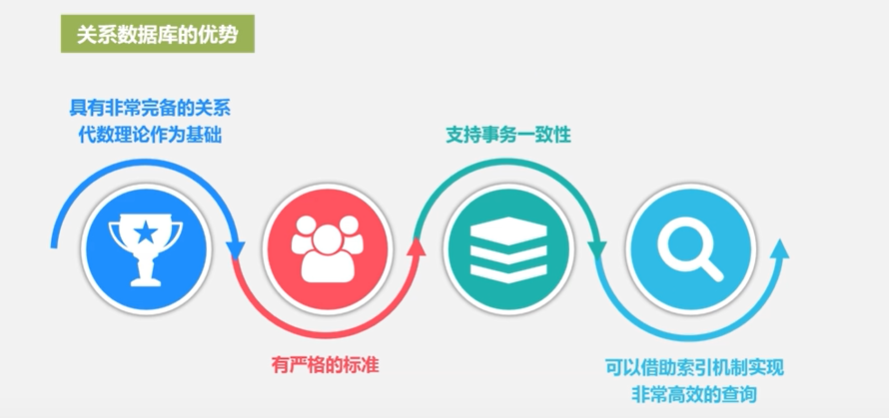
劣势

NoSQL数据库：

两种数据库的应用场景：

NoSQL数据库与关系数据库的比较的更多相关文章

  1. 关于NoSQL数据库你应该知道的10件事

    关系数据库模型已经流行了几十年了,但是一种新类型的数据库——被称为NoSQL,正在引起企业的注意.下面是关于它的优势和劣势的一个概述.二十多年以来,对数据库管理来说,关系数据库(RDBMS)模型一直是 ...

  2. NoSQL数据库探讨之一 － 为什么要用非关系数据库？

    随着互联网web2.0网站的兴起,非关系型的数据库现在成了一个极其热门的新领域,非关系数据库产品的发展非常迅速.而传统的关系数据库在应付 web2.0网站,特别是超大规模和高并发的SNS类型的web2 ...

  3. 关系数据库&&NoSQL数据库

    在过去,我们只需要学习和使用一种数据库技术,就能做几乎所有的数据库应用开发.因为成熟稳定的关系数据库产品并不是很多,而供你选择的免费版本就更加少了,所以互联网领域基本上都选择了免费的MySQL数据库. ...

  4. 关系数据库&&NoSQL数据库

    在过去,我们只需要学习和使用一种数据库技术,就能做几乎所有的数据库应用开发.因为成熟稳定的关系数据库产品并不是很多,而供你选择的免费版本就更加少了,所以互联网领域基本上都选择了免费的MySQL数据库. ...

  5. 大数据技术原理与应用【第五讲】NoSQL数据库：5.1 NoSQL概论&5.2 NoSQL与关系数据库的比较

    5.1 NoSQL概论 最初:反SQL 概念演变,现在:Not only SQL 特点: 1.灵活的可扩展性 所以支持海量数据存储 2.灵活的数据模型 例如:HBase 3.和云计算的紧密结合 (一) ...

  6. NoSql数据库使用半年后在设计上面的一些心得

    NoSql数据库这个概念听闻许久了,也陆续看到很多公司和产品都在使用,优缺点似乎都被分析的清清楚楚.但我心里一直存有一个疑惑,它的出现究竟是为了解决什么问题? 这个疑惑非常大,为此我看了很多分析文章, ...

  7. 小型单文件NoSQL数据库SharpFileDB初步实现

    小型单文件NoSQL数据库SharpFileDB初步实现 我不是数据库方面的专家,不过还是想做一个小型的数据库,算是一种通过mission impossible进行学习锻炼的方式.我知道这是自不量力, ...

  8. NoSQL数据库笔谈（转）

    NoSQL数据库笔谈 databases , appdir , node , paper颜开 , v0.2 , 2010.2 序 思想篇 CAP 最终一致性 变体 BASE 其他 I/O的五分钟法则 ...

  9. NoSQL数据库介绍

    NoSQL在2010年风生水起,大大小小的Web站点在追求高性能高可靠性方面,不由自主都选择了NoSQL技术作为优先考虑的方面.今年伊始,InfoQ中文站有幸邀请到凤凰网的孙立先生,为大家分享他之于N ...

  10. 2013最常用的NoSQL数据库

    摘要:与关系数据库相比,每个NoSQL都有自己不同的适用场景,这里带大家盘点文档数据库.图数据库.键值数据存储.列存储数据库与内存数据网络等领域的常用的NoSQL. 在几年内,NoSQL数据库一直以性 ...

随机推荐

  1. 在.NET Framework中使用RocketMQ（阿里云版）实战【第二章】

    章节 第一章:https://www.cnblogs.com/kimiliucn/p/17662052.html 第二章:https://www.cnblogs.com/kimiliucn/p/176 ...

  2. 使用PIL为图片添加水印

    使用pillow库为图片添加文件或者图片水印 下面是我们想要添加水印的图片: 图片水印: 效果图如下: ps:对图片添加字体时,需指定字体文件,如 simsun.ttc windows中在 C:\Wi ...

  3. SQL注入——搜索型

    SQL注入-搜索型 搜索型注入-原理介绍 一些网站为了方便用户查找网站的资源,都对用户提供了搜索的功能,因为是搜索功能,往往是程序员在编写代码时都忽略了对其变量(参数)的过滤,而且这样的漏洞在国内的系 ...

  4. 提取protobuf定义文件结构

    先安装protobuf的js支持包 npm install protobufjs test.proto文件如下所示 syntax = "proto3"; package Test; ...

  5. .NET周刊【9月第2期 2023-09-10】

    国内文章 使用 OpenTelemetry 构建 .NET 应用可观测性(2):OpenTelemetry 项目简介 https://www.cnblogs.com/eventhorizon/p/17 ...

  6. 使用GPU训练Pytorch模型

    如何使用GPU训练Pytorch模型 这两天的深度学习实验真实让人头疼,传说中的"猫狗大战",对模型的训练用CPU的话9h起步,12h是常态,大学生哪耗得起,因此查找资料搭建了GP ...

  7. 【python】python开源代理ip池

    一.前言 随着互联网的不断发展,越来越多的应用需要使用高匿代理IP才能访问目标网站,而代理IP作为一种能够隐藏本机真实IP地址的工具,在网络抓取.搜索引擎排名.广告投放.反爬虫等方面有着广泛的应用场景 ...

  8. 关于初次new springboot项目

    如果是新手初学,然后做springboot项目报各种错,改来改去最终都无法出现successful字样. 请先检查,maven环境是否配好. maven环境决定你下载依赖的速度,以及能否下载成功. m ...

  9. Python中的转义符\

    1.转义符 可以百度百科查询 2.Python中的转义符 我目前知道的Python中的转义符使用场景有两个:一个是字符串,一个是正则表达式 2.1.字符串的转义 2.1.1.反斜杠"\&qu ...

  10. 普冉PY32系列(八) GPIO模拟和硬件SPI方式驱动无线收发芯片XN297LBW

    目录 普冉PY32系列(一) PY32F0系列32位Cortex M0+ MCU简介 普冉PY32系列(二) Ubuntu GCC Toolchain和VSCode开发环境 普冉PY32系列(三) P ...