一文轻松搞定 tarjan 算法（二）（附带 tarjan 题单）

完结篇：tarjan 求割点、点双连通分量、割边（桥）（附 40 道很好的 tarjan 题目）。

上一篇（tarjan 求强连通分量，缩点，求边双）

tarjan 求割点

还是求强联通分量的大致思路捏.

算法思路：

我们把图中的点分为两种： 每一个联通子图搜索开始的根节点 和 其他点。

判断是不是割点的方式如下：

• 对于根节点：
  
  记一下在跑 tarjan 过程中从这个点出发的未被搜索到的子节点的数量 \(child\)，如果 \(child\ge 2\)，那么这个点为割点，否则就不是割点；

  • 证明（很简单，建议自己先想一想为什么或者手模个图，实在不懂再看证明）：

  设根节点为点 \(u\)，如果 \(child\) 为 1 的话，说明根节点的不同子树上的点可以不经过点 \(u\) 而互相到达，也就是说即使删了 \(u\) 点，图中所有点照样可以互相到达，则 \(u\) 不为割点。反之，同样也易证得为割点。

• 对于其他点：
  
  判断一个点 \(u\) 有没有一个子节点 \(v\) 使得 low[v] >= dfn[u]，若存在，则 \(u\) 为割点，否则不为割点。

  • 证明：

  因为我们在无向图中跑 tarjan 时，已经特判父节点或边的编号来避免走“回头路”了（详见上文求边双部分），所以如果满足判断条件时，说明 \(v\) 通过返祖边只能到达 \(u\) 及其子树部分，并不能到达 \(u\) 的祖先节点，所以若 \(u\) 点删去，那么 \(v\) 点便与 \(u\) 以上部分断开了，此时显然 \(u\) 为割点。

会判断这两类点是不是割点之后就做完了，相信大家也知道该怎么求了。看代码吧！

算法代码：

相比于求边双部分增加了数组 cut[x] 来判断 \(x\) 是不是割点，若为 true 则 \(x\) 是割点，否则不是。

void tarjan(int x, int p){
    low[x] = dfn[x] = ++th;
    s[++top] = x; int child = 0;
    for(int i=head[x]; i; i=nxt[i]){
        int y = to[i];
        if(y == p) continue;
        if(!dfn[y]){
            tarjan(y, x);
            low[x] = min(low[x], low[y]);

            if(low[y] >= dfn[x]){
                child++;
                if(p != 0 or child > 1) cut[x] = 1;
            }
        }
        else low[x] = min(low[x], dfn[y]);
    }
}

为什么 p == 0 说明 \(x\) 为根节点呢，大家肯定知道啦！

因为主函数中是这么写的：

    for(int i=1; i<=n; i++)
        if(!dfn[i]) tarjan(i, 0);

tarjan 求点双连通分量

我该先写求点双好呢还是先写求割边好呢，这俩都是需要割点的相关知识的，啊选择困难症（

但是的但是，学会求割点之后那求点双（简称 BCC）就很简单啦 啦啦小魔仙，玛卡巴卡，卡巴露露，摇身变！

算法思路：

性质：无向连通图中割点一定属于至少两个BCC，非割点只属于一个BCC

如此图：2 号点是个割点，其他点则不是。有红、蓝两个 BCC。

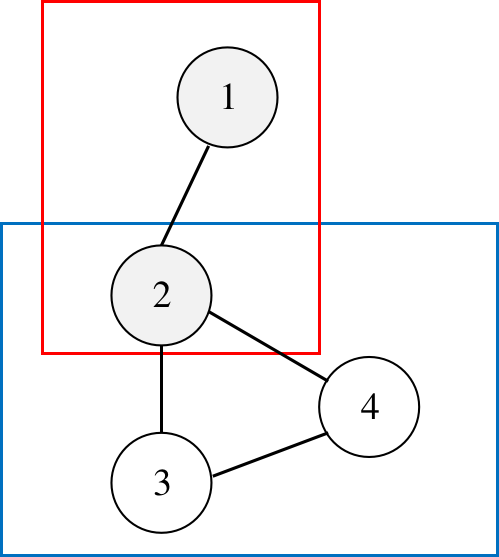
有一条显然的结论：每个点双，它在 dfs 时最先被发现的点一定是割点或者 dfs 树的树根。

证明：这很显然吧？！根据割点的定义自己理解一下，不证明。算了，还是简单说一下吧：我们知道割点是 BCC 的交点，即 BCC 通过割点连接，从一个 BCC 到另一个 BCC 一定是从经过割点开始的，所以证得。

那么这条结论其实就等价于 每个 BCC 都在其最先被发现的点（一个割点或根节点）的子树中。那么我们在上文求割点方法基础上每找到一个割点（或根节点）后，其子树（包含自己）便是一个点双连通分量了。

实现：

我们还是维护一个栈，存点，每当搜索到一个点时就将该点入栈，找到割点（就是找到一个 BCC）时将栈顶到该割点所有元素依次出栈，（但注意：割点并不出栈，因为上文已说一个割点属于两个 BCC，它还需要来更新另一个 BCC，所以先不出栈，特判就行。）那么出栈的元素以及割点就是所求的点双了。

算法演示：

如上图中，我们以 1 为根开始搜索；

搜索到 2 节点时，继续递归 2 -> 3 -> 4；发现 \(low_4 = 2 < dfn_3\)，那么 3 号点则不是割点，回溯；

而 \(low_3 = dfn_2\)，所以 \(2\) 号点是割点，那么将此时栈中从栈顶到 \(2\) 号点所有元素出栈形成点双；

此时栈从栈尾到栈顶依次是：1，2，3，4。那么便是 2，3，4 构成一个点双（但 2 还在栈中）。

继续回溯到 2 -> 1；发现 1 号点是根节点，也将栈中元素出栈（这时 1 是根节点，所以 1 也出栈），那么 1，2 就又构成了一个点双。

算法代码：

void tarjan(int x, int p){
    low[x] = dfn[x] = ++th;
    s[++top] = x;
    if(!p and !head[x]){ // 特判孤点
        BCC[++bcc].emplace_back(x);
        top--; return;
    }
    for(int i=head[x]; i; i=nxt[i]){
        int y = to[i];
        if(y == p) continue;
        if(!dfn[y]){
            tarjan(y, x);
            low[x] = min(low[x], low[y]);
            if(low[y] >= dfn[x] or !p){ //是割点或者根节点
                ++bcc;
                do BCC[bcc].emplace_back(s[top]);
                while(s[top--] != y);
                BCC[bcc].emplace_back(x);
            }
        }
        else low[x] = min(low[x], dfn[y]);
    }
}

例题：

【模板】点双连通分量

板子题练练手。注意这题需要判孤点情况。

tarjan 求割边（桥）

太简单啦！

和割点差不多，改一条：low[y] > dfn[x]，并且不需要特判根节点了（因为 边 != 点）。

解释：（在判边保证不走回头路的条件下）\(low_y = dfn_x\) 时，说明不通过从 \(x -> y\) 这条路径， \(y\) 也照样可以回到 \(x\) 节点，那么就保证从 \(y\) 到 \(x\) 有两条路径可走了，所以 \(x->y\) 这条路不是割边。

那么完了！

算法代码：

cut[i] = true; 表示 \(i\) 这条路为割边。

void tarjan(int x, int p){
    low[x] = dfn[x] = ++th;
    s[++top] = x;
    for(int i=head[x]; i; i=nxt[i]){
        int y = to[i];
        if(y == p) continue;
        if(!dfn[y]){
            tarjan(y, x);
            low[x] = min(low[x], low[y]);
            if(low[y] > dfn[x]){
                cut[i] = true;
            }
        }
        else low[x] = min(low[x], dfn[y]);
    }
}

题目练习：

这有个很好的tarjan 题单，从模板到进阶，题都很好，推荐给大家。

所含题目如下

P1656 炸铁路

P1455 搭配购买

P3916 图的遍历

P2835 刻录光盘

P1073 [NOIP2009 提高组] 最优贸易

P2863 [USACO06JAN]The Cow Prom S

P8436 【模板】边双连通分量

P8287 「DAOI R1」Flame

P2002 消息扩散

P2341 [USACO03FALL / HAOI2006] 受欢迎的牛 G

P3387 【模板】缩点

P3388 【模板】割点（割顶）

P8435 【模板】点双连通分量

P1407 [国家集训队]稳定婚姻

P2194 HXY烧情侣

P2746 [USACO5.3]校园网Network of Schools

P2812 校园网络【[USACO]Network of Schools加强版】

P2941 [USACO09FEB]Surround the Islands S

P2860 [USACO06JAN]Redundant Paths G

P3398 仓鼠找 sugar

P2169 正则表达式

P3627 [APIO2009] 抢掠计划

P2656 采蘑菇

P4306 [JSOI2010]连通数

P5676 [GZOI2017]小z玩游戏

P1656 炸铁路

P1455 搭配购买

P3916 图的遍历

P2835 刻录光盘

P1073 [NOIP2009 提高组] 最优贸易

P2863 [USACO06JAN]The Cow Prom S

P8436 【模板】边双连通分量

P8287 「DAOI R1」Flame

P2002 消息扩散

P2341 [USACO03FALL / HAOI2006] 受欢迎的牛 G

P3387 【模板】缩点

P3388 【模板】割点（割顶）

P8435 【模板】点双连通分量

P1407 [国家集训队]稳定婚姻

P2194 HXY烧情侣

P2746 [USACO5.3]校园网Network of Schools

P2812 校园网络【[USACO]Network of Schools加强版】

P2941 [USACO09FEB]Surround the Islands S

P2860 [USACO06JAN]Redundant Paths G

P3398 仓鼠找 sugar

P1262 间谍网络

P4742 [Wind Festival]Running In The Sky

P8867 [NOIP2022] 建造军营

P3469 [POI2008]BLO-Blockade

P2515 [HAOI2010]软件安装

P5058 [ZJOI2004]嗅探器

P7687 [CEOI2005] Critical Network Lines

P7924 「EVOI-RD2」旅行家

P5236 【模板】静态仙人掌

P3225 [HNOI2012]矿场搭建

P4716 【模板】最小树形图

P4126 [AHOI2009]最小割

P6335 [COCI2007-2008#1] STAZA

P4637 [SHOI2011]扫雷机器人

P5236 【模板】静态仙人掌

P4716 【模板】最小树形图

P4436 [HNOI/AHOI2018]游戏

End

历时多天，终于把这两篇 tarjan 写完了。

tarjan 都学了，那下一章包得是圆方树的啦（

\(敬请期待......\)