数据结构之B树

1 引言

B-tree，B即Balanced，是自平衡的多叉搜索树，用于组织和存储大量数据，以及数据库和文件系统等需要高效查找和插入操作的应用中。

为什么是“大量数据”？当主存不足以放入大量数据时，不常用的数据应存储于外存，而访问外存有额外时间开销（如磁盘转动时间、磁头移动时间等），于是我们需要一个数据结构来减少磁盘访问次数。

B树每个节点包含多个关键字（键）和对应的数据指针（节点），关键字按照大小排序，并且每个节点的关键字都对应子节点的范围。

B树的根节点存储在主存中，而其他节点存储在磁盘或其他外部存储设备上。

M阶B树是有以下特性的M叉树：

1. 数据项（data items）存储在叶节点（leaves）；
2. 非叶节点（nonleaf nodes）最多存储指引搜索路线的M-1个关键字Key，并且Key i是该节点子树i+1的最小值；
3. 根节点（root）也是非叶节点，它有2至M个子节点；
4. 所有非叶节点（root除外）有\(\lceil M/2 \rceil\)至M个子节点；
5. 所有叶节点都位于最底层，有\(\lceil L/2 \rceil\)至L个数据项。L是指定值，由存储块和记录大小决定，即L=存储块大小/记录大小。

五阶B树示例如下图所示：

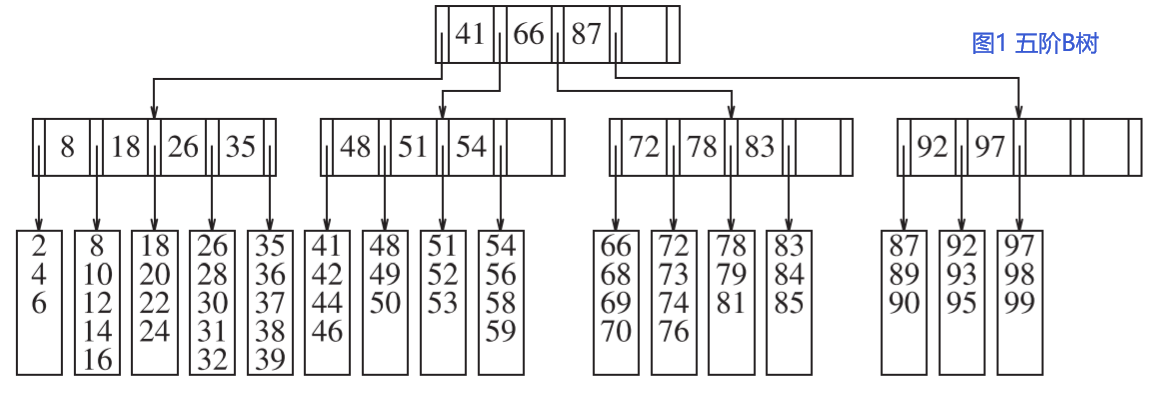
上图中，M=5，L=5，于是，根节点有2到5个子节点，非叶节点最多有4个关键字，除根节点外的非叶结点有3到5个子节点，叶节点有3到5个数据项。每个节点都是一个磁盘块（disk block）。

2 B树的操作

添加

如图2，插入57到图1。

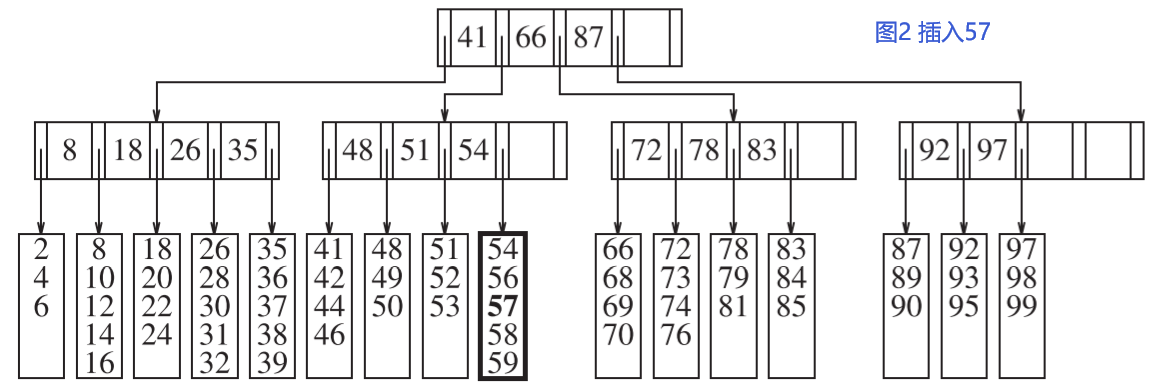
插入操作步骤如下：

1. 从根节点开始，按照键值的大小进行搜索，直到找到合适的叶子节点。在这个例子中，我们找到了可以插入57的叶子节点。
2. 检查叶子节点是否已满。如果叶子节点未满，则可以直接将57插入到适当的位置。
3. 如果叶子节点已满，需要进行节点的分裂操作。首先，将叶子节点中的数据项和新的数据项按照键值的顺序重新排序。然后，将前一半数据项保留在原始叶子节点中，将后一半数据项移动到新创建的叶子节点中。同时，更新父节点中的键值和分支信息，以反映新的叶子节点的存在。
4. 如果父节点也已满，可能需要继续进行分裂操作，以保持B树的平衡性。

如图3，插入55到图2，共两步：分裂页节点和更新父节点。所以一共有三次disk write操作。

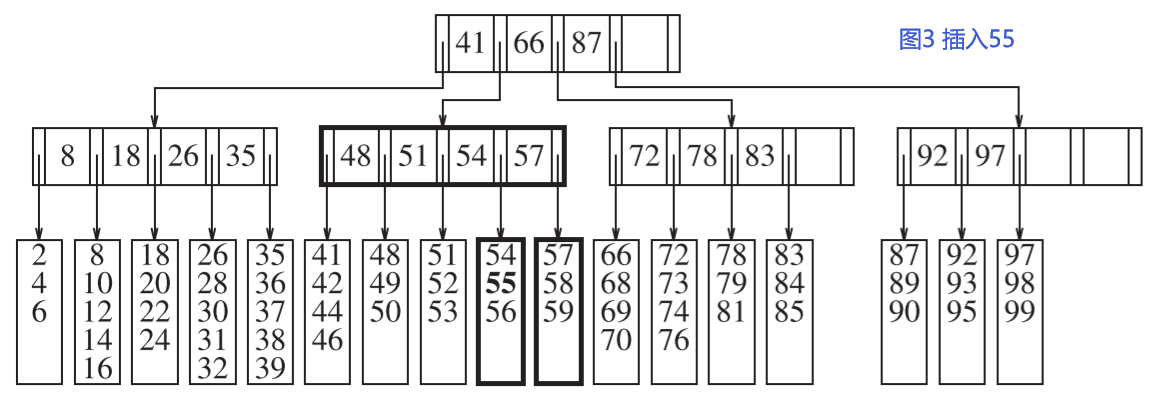
如图4，插入40到图3，由于父节点满项，所以除了分裂子节点，更新父节点，还需要再分裂父节点。一共五次disk write。

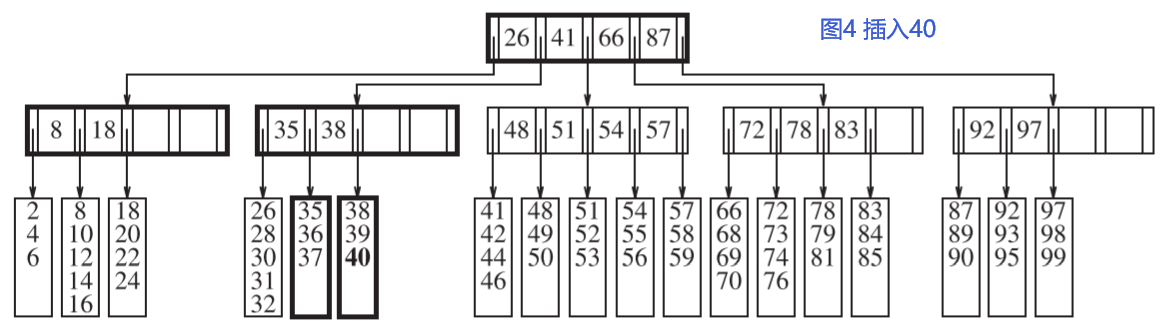
添加操作可能导致的根节点分裂是B树高度增加唯一方式。

删除

flowchart TD
A(寻找键值) ==> B{是否存在}
B ==是==> C[删除键值]
B ==否==> D(结束)
C ==> E{该节点是否符合最小占用}
E ==是==> D
E ==否==> F{邻居节点是否比最小占用多}
F ==是==> G[从邻居节点借一个]
F ==否==> H[合并邻居节点]
G ==> D
H ==> I{父节点是否符合最小占用}
I ==是==> D
I ==否==> J{是否为根节点}
J ==否==> F
J ==是==> K{根节点是否只有一个子节点}
K ==否==> D
K ==是==> L[删除根节点,子节点作为新根节点]
L ==> D

上图删除根节点是B树高度减小的唯一方式。