POJ 3249 Test for Job

Test for Job

Time Limit: 5000MS		Memory Limit: 65536K
Total Submissions: 13457		Accepted: 3100

Description

Mr.Dog was fired by his company. In order to support his family, he must find a new job as soon as possible. Nowadays, It's hard to have a job, since there are swelling numbers of the unemployed. So some companies often use hard tests for their recruitment.

The test is like this: starting from a source-city, you may pass through some directed roads to reach another city. Each time you reach a city, you can earn some profit or pay some fee, Let this process continue until you reach a target-city. The boss will compute the expense you spent for your trip and the profit you have just obtained. Finally, he will decide whether you can be hired.

In order to get the job, Mr.Dog managed to obtain the knowledge of the net profit V_i of all cities he may reach (a negative V_i indicates that money is spent rather than gained) and the connection between cities. A city with no roads leading to it is a source-city and a city with no roads leading to other cities is a target-city. The mission of Mr.Dog is to start from a source-city and choose a route leading to a target-city through which he can get the maximum profit.

Input

The input file includes several test cases.
The first line of each test case contains 2 integers n and m(1
≤ n ≤ 100000, 0 ≤ m ≤ 1000000) indicating the number of cities
and roads.
The next n lines each contain a single integer. The ith line
describes the net profit of the city i, V_i (0 ≤ |V_i|
≤ 20000)
The next m lines each contain two integers x, y indicating
that there is a road leads from city x to city y. It is
guaranteed that each road appears exactly once, and there is no way to
return to a previous city.
　

Output

The output file contains one line for each test cases, in which contains an
integer indicating the maximum profit Dog is able to obtain (or the minimum
expenditure to spend)

Sample Input

Sample Output

Hint

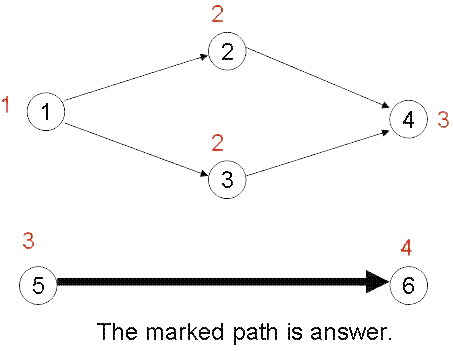
Source

POJ Monthly--2007.07.08, 落叶飞雪

【题意】

给n个点，m条单向边，每个点有点权，没有边权，然后遍历

一条路径：以任意一个入度为0的点为起点，沿着单向边走，走到任意一个出度为0的点为终点，路径长度为经过个点的点权之和。

求最长路径。

【分析】

一开始想的是拓扑排序，分离出起点和终点，然后dijkstra跑一遍。结果，无论算时间复杂度，还是实际交付评测，都会T。

然后，再读题目，发现每个点的后继都唯一，然后，满足无后效性，猜想DP，递推代码不好打，直接从每个起点记忆话搜索，跑最长路。

保证时间复杂度：O(m)

【代码】

#include<vector>

#include<cstdio>

#include<cstring>

#include<iostream>

#define m(s) memset(s,0,sizeof s)

using namespace std;

const int N=1e5+5;

int n,m,val[N],du[N],f[N];

vector<int>e[N];

inline void Clear(){

	m(du);m(f);

	for(int i=1;i<=n;i++) e[i].clear();

}

inline void Init(){

	for(int i=1;i<=n;i++) scanf("%d",val+i);

	for(int i=1,x,y;i<=m;i++) scanf("%d%d",&x,&y),du[y]++,e[x].push_back(y);

}

int dfs(int x){

	int &now=f[x];

	if(now) return now;

	now=-2e9;

	if(!e[x].size()) return now=val[x];

	for(int i=0;i<e[x].size();i++){

		int v=e[x][i];

		now=max(now,val[x]+dfs(v));

	}

	return now;

}

inline void Solve(){

	int ans=-2e9;

	for(int i=1;i<=n;i++){

		if(!du[i]){

			ans=max(ans,dfs(i));

		}

	}

	printf("%d\n",ans);

}

int main(){

	while(scanf("%d%d",&n,&m)==2){

		Clear();

		Init();

		Solve();

	}

	return 0;

}