POJ 2663 Tri Tiling

                                                                                Tri Tiling

 

Time Limit: 1000MS		Memory Limit: 65536K
Total Submissions: 10306		Accepted: 5237

Description

In how many ways can you tile a 3xn rectangle with 2x1 dominoes? 
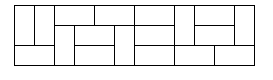
Here is a sample tiling of a 3x12 rectangle. 

Input

Input consists of several test cases followed by a line containing -1. Each test case is a line containing an integer 0 <= n <= 30.

Output

For each test case, output one integer number giving the number of possible tilings.

Sample Input

2
8
12
-1

Sample Output

3
153
2131

这是一维动态规划的一道非常经典的题目

如果n为奇数，必然无解。

当n为偶数时，一个比较直观的思路就是把大矩形用竖线切出左边一部分，然后递归求解，就像UVA_10359那样，直接考虑最左边一个小矩形是如何构成的我们就可以递归得到f(n)递推式。

虽然这个题目乍看上去小矩形似乎拼法比较多，而且要拼出一个不能再用竖线切分的小矩形似乎拼的方法也并不直观。但如果我们在纸上多画一画的话，对于拼任意一个横向边长为x的不可再用竖线切分的小矩形，如果x为2，显然有3种拼法，如果x为大于2的偶数，那么只有2种拼法。

至于如果x>2为什么只有两种拼法，我们不妨实际拼一下。首先第一列肯定只有两种情况，第一种是一个横的在上面，然后一个竖的在左下方，第二种是一个横的在下面，然后一个竖的在左上方，因为两种情况对称，我们只讨论第一种情况。

现在已经拼好两个了，如果横的下面再放一个竖的，那么显然这个就成了一个x=2的小矩形了，那么最后拼出来的就不符合我们前面说的不可再用竖线切分的特征了，因此横的下面也即竖的右边，只能再放两个横的，放完两个横的我们就发现两个横的上面有一个小正方形区域，这个区域只能楔进去一个横的，等把这个横的画完之后，My God，我们会发现一个惊人的事实，现在的这个结构是和我们最初放完一个横的一个竖的的那种情况的结构是一样的！因此，如果我们想继续向右拼出不能被竖线切分的矩形，那么只能是重复之前的操作，因而得到的最后横向边长为x的矩形是唯一确定的。

前面我们最初拼的时候只取了对称的两种情况之一，因此，如果x>2，拼出一个不能被竖线切割的矩形的方法只有两种。

那么递推公式自然就有了，f(n)=3*f(n-2)+2*f(n-4)+…+2*f(0)，然后再写出f(n-2)的递推式后两式作差就可以得到f(n)=4*f(n-2)-f(n-4)，递归的边界是f(0)=1，f(2)=3

 #include<iostream>
 using namespace std;
 int main(){
     int num[];
     int i;
     num[]=;
     num[]=;
     for(i=;i<;i=i+)
         num[i]=*num[i-]-num[i-];
     int n;
     while(cin>>n){
         if(n==-)
             break;
         if(n%==)
             cout<<num[n]<<endl;
         else
             cout<<""<<endl;
     }
     return ;
 }