[UFLDL] Linear Regression & Classification

博客内容取材于：http://www.cnblogs.com/tornadomeet/archive/2012/06/24/2560261.html

Deep learning：六(regularized logistic回归练习)

Deep learning：五(regularized线性回归练习)

Deep learning：四(logistic regression练习)

Deep learning：三(Multivariance Linear Regression练习)

Deep learning：二(linear regression练习)

outline

参考资料：

Comment: 难点不多，故补充CMU 10-702线性部分的章节。

本文主要是个概括，具体内容还需要看具体章节讲解。

概念辨析

线性拟合是线性回归么？

回归，仅表示一个“repeative 回归过程”，或者叫做“回归模型”。

至于要解决什么问题，这要取决于 solver。

基本问题

Ref: https://www.zhihu.com/question/21329754

- Logistic Regression 分类问题
- Linear Regression 拟合问题

- Support Vector Regression 拟合问题
- Support Vector Machine 分类问题

- Naive Bayes 拟合/分类都可以

- A multilayer perceptron (MLP)
- 前馈神经网络(如 CNN 系列) 用于分类和回归
- 循环神经网络(如 RNN 系列) 用于分类和回归

拟合：线性回归

简单模式：一元线性回归问题（一个因子）

Ref: Deep learning：二(linear regression练习)

求：孩子的年纪和身高的关系，training过程。

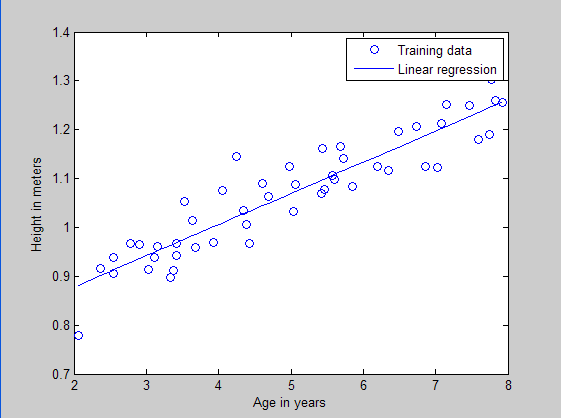
进阶模式：多元线性回归问题（两个因子）

Ref: 三(Multivariance Linear Regression练习)

【损失函数】其向量表达形式如下：

【参数更新】当使用梯度下降法进行参数的求解时，参数的更新公式如下：

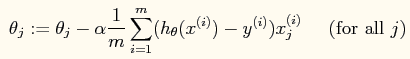
就是感知器，一点小区别的是：1/m有没有必要的问题。

分类：线性分类

二分类 - 逻辑回归

基本原理

Ref: 四(logistic regression练习)

Ref: 一文读懂逻辑回归【比较全面】

【损失函数】采用cross-entropy as loss function:

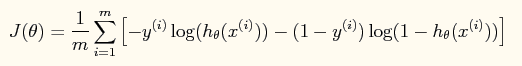
　　【参数更新】如果采用牛顿法来求解回归方程中的参数，则参数的迭代公式为：

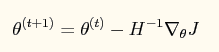
　　其中一阶导函数和hessian矩阵表达式如下：

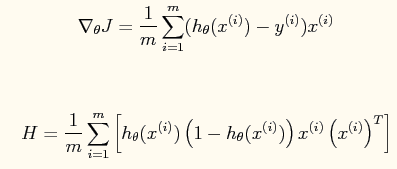
线性不可分 - 升维

五(regularized线性回归练习)

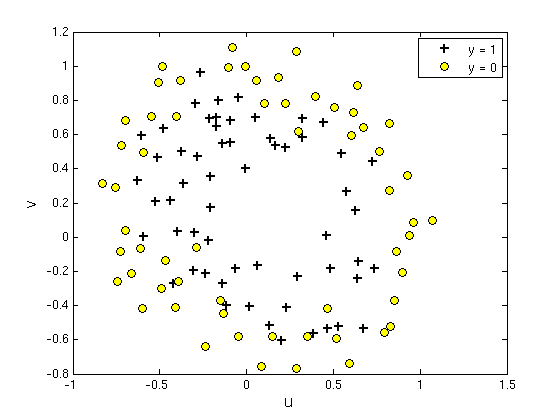
具有2个特征的一堆训练数据集，从该数据的分布可以看出它们并不是非常线性可分的，因此很有必要用更高阶的特征来模拟。

如下用到了特征值的5次方来求解。【升维的意义和思路】

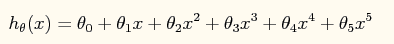
"正则项" 的意义

六(regularized logistic回归练习)

Regularization项在分类问题中（logistic回归）的应用。

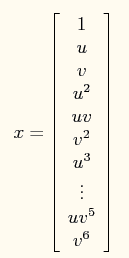
没正则项：

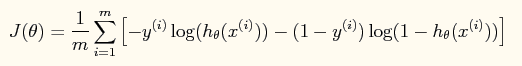
有正则项：

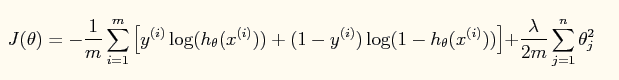
Weight Decay: lamda的选择也可以看作是模型的选择。

小总结：

注意对比”拟合“与“分类”的公式表达的区别。

sigmoid + xentropy算是绝配。

多分类 - Softmax Regression

Ref: 十三(Softmax Regression)

Ref: 十四(Softmax Regression练习)

多分类问题，共有k个类别。在softmax regression中这时候的系统的方程为：

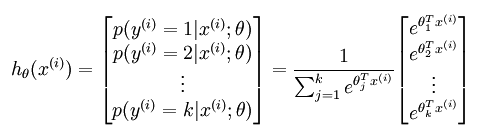
其中的参数sidta不再是列向量，而是一个矩阵，矩阵的每一行可以看做是一个类别所对应分类器的参数【the parameters on edges (fan in) of Output Layer】，总共有k行。

所以矩阵sidta可以写成下面的形式：

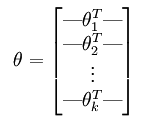
【theta_i就是fan in的各个边的权重们】

“指数分布就有失忆性”

比较有趣的时，softmax regression中对参数的最优化求解不只一个，每当求得一个优化参数时，如果将这个参数的每一项都减掉同一个数，其得到的损失函数值也是一样的。

这说明这个参数不是唯一解。用数学公式证明过程如下所示：

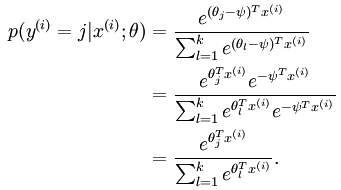
从宏观上可以这么理解，因为此时的损失函数不是严格非凸的，也就是说在局部最小值点附近是一个”平坦”的，所以在这个参数附近的值都是一样的了。

那么怎样避免这个问题呢？加入规则项就可以解决。

比如说，用牛顿法求解时，hession矩阵如果没有加入规则项，就有可能不是可逆的从而导致了刚才的情况，如果加入了规则项后该hession矩阵就不会不可逆。

损失函数的方程对比：【1{.}是一个指示性函数】

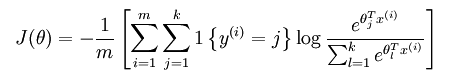
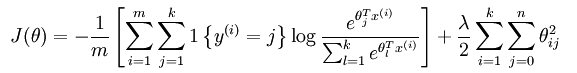
偏导函数对比：

如果要用梯度下降法，牛顿法，或者L-BFGS法求得系统的参数的话，就必须求出损失函数的偏导函数，softmax regression中损失函数的偏导函数如下所示：

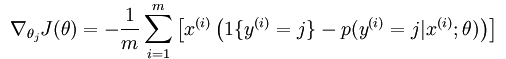
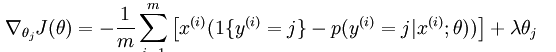
网页教程中还介绍了softmax regression和k binary classifiers之间的区别和使用条件。总结就这么一个要点：

- 如果所需的分类类别之间是严格相互排斥的，也就是两种类别不能同时被一个样本占有，这时候应该使用softmax regression。[one-hot，严格互斥]
- 如果所需分类的类别之间允许某些重叠，这时候就应该使用binary classifiers了。[sigmoid本来就有中间地带]