异常检测LOF

局部异常因子算法-Local Outlier Factor(LOF)
在数据挖掘方面，经常需要在做特征工程和模型训练之前对数据进行清洗，剔除无效数据和异常数据。异常检测也是数据挖掘的一个方向，用于反作弊、伪基站、金融诈骗等领域。

异常检测方法，针对不同的数据形式，有不同的实现方法。常用的有基于分布的方法，在上、下α分位点之外的值认为是异常值（例如图1），对于属性值常用此类方法。基于距离的方法，适用于二维或高维坐标体系内异常点的判别，例如二维平面坐标或经纬度空间坐标下异常点识别，可用此类方法。

这次要介绍一下一种基于密度的异常检测算法，局部异常因子LOF算法（Local Outlier Factor）

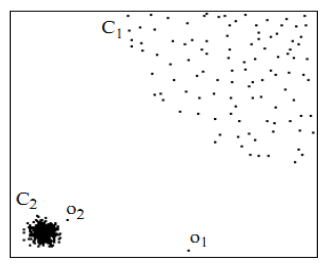
用视觉直观的感受一下，如图2，对于C1集合的点，整体间距，密度，分散情况较为均匀一致，可以认为是同一簇；对于C2集合的点，同样可认为是一簇。o1、o2点相对孤立，可以认为是异常点或离散点。现在的问题是，如何实现算法的通用性，可以满足C1和C2这种密度分散情况迥异的集合的异常点识别。LOF可以实现我们的目标。

下面介绍LOF算法的相关定义：
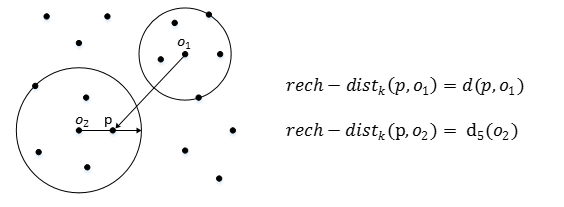
　　1) d(p,o)：两点p和o之间的距离。
　　2) k-distance：第k距离
　　　　对于点p的第k距离dk(p)定义如下：
　　　　dk(p)=d(p,o)，并且满足：
　　　　　　a) 在集合中至少有不包括p在内的k个点o' ∈ C{x ≠ p}， 满足d(p,o') ≤ d(p,o) 。
　　　　　　b) 在集合中最多有不包括p在内的k−1个点o' ∈ C{x ≠ p}，满足d(p,o') < d(p,o)。

如下图，离p第5远的点在以p为圆心，d5(p)为半径的

　　3) k-distance neighborhood of p：第k距离邻域
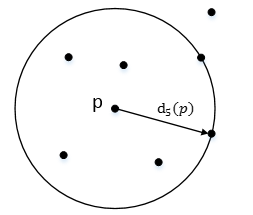
　　　　点p的第k距离邻域Nk(p)，就是p的第k距离即以内的所有点，包括第k距离。
　　　　因此p的第k邻域点的个数 |Nk(p)| ≥ k。
　　4) reach-distance：可达距离
　　　　点o到点p的第k可达距离定义为：reach−distancek(p,o) = max{dk(o), d(p,o)}
　　　　也就是，点o到点p的第k可达距离，至少是o的第k距离，或者为o、p间的真实距离。
　　　　
　　5) local reachability density：局部可达密度
　　　　点ｐ的局部可达密度表示为：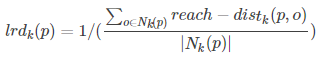
　　　　表示点p的第k邻域内的点到p的平均可达距离的倒数。

　　6) local outlier factor：局部离群因子
　　　　点p的局部离群因子表示为：
　　　　表示点p的邻域点Nk(p)的局部可达密度与点p的局部可达密度之比的平均数。

　　　　local outlier factor越接近1，说明p的其邻域点密度差不多，p可能和邻域同属一簇；

　　　　local outlier factor越小于1，说明p的密度高于其邻域点密度，p为密集点；

　　　　local outlier factor越大于1，说明p的密度小于其邻域点密度，p越可能是异常点。

因为LOF对密度的是通过点的第k邻域来计算，而不是全局计算，因此得名为“局部”异常因子，这样，对于图1的两种数据集C1和C2，LOF完全可以正确处理，而不会因为数据密度分散情况不同而错误的将正常点判定为异常点。

转自：https://blog.csdn.net/wangyibo0201/article/details/51705966