BZOJ1040 [ZJOI2008]骑士 基环树林(环套树) 树形动态规划

欢迎访问~原文出处——博客园-zhouzhendong

去博客园看该题解

---

题意概括

有n个人，每一个人有一个最恨的人。

并且，每一个人有一个权值。

一个人不可以和他最恨的人同时被选中。

现在请你求出在这n个人中选出一些人，使得其权值和最大。

（题解在“心塞史”后面）

---

心塞史

注：蒟蒻第一次遇见这种基环树题QAQ。

先看样例。

3

10 2

20 3

30 1

Ⅰ

瞬间开心。

随便选了一道，居然是水题？

这种类似的题目我貌似做过，好像是找几个环就可以了？

当然，于是我找完环，打完线性动归，一交wa掉，才发现错了。约2000B。

Ⅱ

然而可怕的事情没这么容易结束。

我灵机一动~哦！不就是环再连一条线出去嘛……

分3种情况dp一下就可以了。

于是又wa掉了。约2500B。

Ⅲ

不过事情总是有转机的。

终于发现这是一道树形dp题，只不过有基环树林(环套树，而且是森林)。

理了2个小时思路，证明了一个连通分量中有且仅有一个环（应该没有自环，一个人总不至于恨自己吧）。

然后开开心心的编。一开始我还以为这一题卡栈空间，为了不用手工扩栈这种卑（ji）鄙（zhi）的手段，我打了bfs序写树形dp。结果有情况没考虑，一发wa掉。3000B

Ⅳ

第二天重看这一题。

之前的代码居然一点都看不懂，于是果断again。最终过了。

---

题解

这一题是一道基环树林的树形动归题。

我们按照最恨的人建边。

首先，我们可以分析，这个图虽然看似是有向的，实际上是无向的。

那么，两个不同的连通分量是互不影响的。所以我们下面只考虑一个连通分量。对于每一个连通分量，把结果加起来就可以了。

对于一个连通分量，总共有n条边。如果只有n-1条边，那么显然是一棵树。

但是多了一条边，那么这棵树中一定会出现一个环。

有，且仅有一个环！

如果不考虑环，只考虑树，那么我们明显可以写一份树形dp。

用dp[i][0]表示节点i不取的最大权值和，dp[i][1]表示取节点i的最大权值和。

那么设S为节点i的儿子集合，那么，

有dp[i][0] = Σmax(dp[x][0] , dp[x][1])  x∈S

dp[i][1] = Σdp[x][0]  x∈S

那么有环的情况怎么办？

其实就是在树形dp的基础上，再限制两个节点不能同时为1。那么实际上我们可以特殊标记。

我们可以先找出环，然后断环，然后分别以环的两个端点为根跑一次树形dp。

但是事情没这么简单。

我们认为不为根的那个端点一定不取，那么我们只要在求完该子树的时候，把它的dp[][0]赋值为-INF即可。

关键是，我们不能随随便便的不取某一个点。

比如说这样一个图：

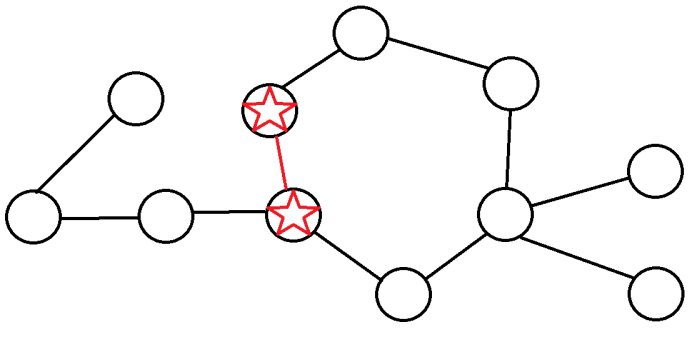
我假设以红色边断开，上面那个节点为根。

我们不可以不访问下面那个。我们要dp。

但是，我们也不能通过两个五角星之间的连边互相访问。

于是我们要判断边。

这里又有一个问题了。

聪（lan）明（duo）的我一开始选择了记录两个端点。

然后莫名wa掉了。

呵呵，对着hzwer大佬的标算对拍了一会儿。排出一组数据。

是这样的：

两个人互相恨对方。任何我保存点的方法就wa掉了。因为他们之间有两条无向边，一条是找环的时候剪掉的，一条其实还是留着的，然而都被我当作没有了。

所以我只能写了记录边的，好像改变不是很大。

我想找个环的事情总不用说了吧？既然你来做这题了，至少应该会找环吧?。

该程序挺繁的，100w个数字，建议读入优化。

代码

#pragma comment(linker, "/STACK:1024000000,1024000000")
#include <cstring>
#include <algorithm>
#include <cstdio>
#include <cstdlib>
#include <cmath>
using namespace std;
typedef long long LL;
bool isd(char ch){return ''<=ch&&ch<='';}
void read(int &x) {x=;char ch=getchar();while (!isd(ch))ch=getchar();while (isd(ch))x=x*+ch-,ch=getchar();}
void readLL(LL &x){x=;char ch=getchar();while (!isd(ch))ch=getchar();while (isd(ch))x=x*+ch-,ch=getchar();}
LL max(LL a,LL b){
    return a>b?a:b;
}
const LL N=+,M=N*,INF=N*N;
struct Gragh{
    int cnt,x[M],y[M],nxt[M],fst[N];
    void set(){
        cnt=;
        memset(fst,,sizeof fst);
    }
    void add(int a,int b){
        y[++cnt]=b,x[cnt]=a;
        nxt[cnt]=fst[a],fst[a]=cnt;
    }
}g;
LL v[N],dp[N][];
int n,p[N],head,tail,fa[N],q[N],vis[N],vis_cnt,dis_use_point;
int pointx,pointy,del_point,del_e;
void dfs(int prev,int rt){
    dp[rt][]=,dp[rt][]=v[rt];
    for (int i=g.fst[rt];i;i=g.nxt[i]){
        int y=g.y[i];
        if (y==prev||i==del_e||(i^)==del_e)
            continue;
        dfs(rt,y);
        dp[rt][]+=max(dp[y][],dp[y][]);
        dp[rt][]+=dp[y][];
    }
    if (rt==del_point)
        dp[rt][]=-INF;
}
LL solve(int root){
    head=tail=;
    q[++tail]=root,vis[root]=vis_cnt;
    fa[root]=;
    pointx=pointy=del_point=;
    while (head<tail)
        for (int x=q[++head],i=g.fst[x];i;i=g.nxt[i]){
            int y=g.y[i];
            if (y==fa[x])
                continue;
            if (vis[y]==vis_cnt){
                pointx=x,pointy=y;
                del_e=i;
                continue;
            }
            vis[y]=vis_cnt;
            fa[y]=x;
            q[++tail]=y;
        }
    for (int i=;i<=tail;i++)
        dp[q[i]][]=dp[q[i]][]=;
    del_point=pointx;
    dfs(,pointy);
    LL ans1=max(dp[pointy][],dp[pointy][]);
    for (int i=;i<=tail;i++)
        dp[q[i]][]=dp[q[i]][]=;
    del_point=pointy;
    dfs(,pointx);
    LL ans2=max(dp[pointx][],dp[pointx][]);
    return max(ans1,ans2);
}
int main(){
    read(n);
    for (int i=;i<=n;i++)
        readLL(v[i]),read(p[i]);
    g.set();
    for (int i=;i<=n;i++)
        g.add(i,p[i]),g.add(p[i],i);
    memset(vis,,sizeof vis);
    vis_cnt=;
    LL ans=;
    for (int i=;i<=n;i++){
        if (vis[i])
            continue;
        vis_cnt++;
        ans+=solve(i);
    }
    printf("%lld",ans);
    return ;
}