深度学习：Sigmoid函数与损失函数求导

1、sigmoid函数

​ sigmoid函数，也就是s型曲线函数，如下：

函数：

导数：

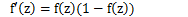
​ 上面是我们常见的形式，虽然知道这样的形式，也知道计算流程，不够感觉并不太直观，下面来分析一下。

1.1 从指数函数到sigmoid

​ 首先我们来画出指数函数的基本图形：

​ 从上图，我们得到了这样的几个信息，指数函数过(0,1)点，单调递增/递减，定义域为(−∞,+∞)，值域为(0,+∞)，再来我们看一下sigmoid函数的图像：

​

​ 如果直接把e−x放到分母上，就与ex图像一样了，所以分母加上1，就得到了上面的图像，定义域是(−∞,+∞)，值域是(0,1)，那么就有一个很好地特性了，就是不管x是什么，都可以得到(0,1)之间的值；

1.2 对数函数与sigmoid

​ 首先来看一下对数函数的图像：

​ 对数函数的图像如上，单调递减，有一个比较好的特性就是在(0,1)之间，在接近0的时候，就近无穷大，接近1的时候为0，如果我们把前面的sigmoid函数放到自变量的位置上，就得到了(0,1)的图像；

​ 我们如何来衡量一个结果与实际计算值得差距呢？一种思路就是，如果结果越接近，差值就越小，反之越大，这个函数就提供了这样一种思路，如果计算得到的值越接近1，那么那么表示与世界结果越接近，反之越远，所以利用这个函数，可以作为逻辑回归分类器的损失函数，如果所有的结果都能接近结果值，那么就越接近于0，如果所有的样本计算完成以后，结果接近于0，就表示计算结果与实际结果非常相近。

2、sigmoid函数求导

​ sigmoid导数具体的推导过程如下：

3、神经网络损失函数求导

​ 神经网络的损失函数可以理解为是一个多级的复合函数，求导使用链式法则。

先来说一下常规求导的过程：

​ e=(a+b)(b+1)

​ 这是一个简单的复合函数，如上图所示，c是a的函数，e是c的函数，如果我们用链式求导法则，分别对a和b求导，那么就是求出e对c的导数，c对a的导数，乘起来，对b求导则是求出e分别对c和d的导数，分别求c和d对b的导数，然后加起来，这种方法使我们常规的做法，有一个问题就是，我们在求到的过程中，e对c求导计算了2次，如果方程特别复杂，那么这个计算量就变得很大，怎样能够让每次求导只计算一次呢？

​

​ 如上图所示，我们从上往下开始计算，将每个单元的值计算出来，然后计算每个单元的偏导数，保存下来；

​ 接下来继续计算子单元的值，子单元的偏导数，保存下来；将最后的子单元到根节点所在的路径的所有偏导乘起来，就是该函数对这个变量的偏导，计算的本质就是从上往下，计算的时候将值存起来，乘到后面的单元上去，这样每个路径的偏导计算只需要一次，从上到下计算一遍就得到了所有的偏导数。

​ 实际上BP(Backpropagation，反向传播算法)，就是如此计算的，如果现在有一个三层的神经网络，有输入、一个隐藏层，输出层，我们对损失函数求权重的偏导数，它是一个复杂的复合函数，如果先对第一层的权重求偏导，然后在对第二层的权重求偏导，会发现，其中有很多重复计算的步骤，就像上面的简单函数的示例，所以，为了避免这种消耗，我们采用的就是从后往前求偏导，求出每个单元的函数值，求出对应单元的偏导数，保存下来，一直乘下去，输入层。

​ 下面用一个简单的示例来演示一下反向传播求偏导的过程：

​ 那么我们会有两个初始的权重矩阵：

​ 我们得到了上面的矩阵，现在我们以sigmoid函数作为激活函数，分别来计算每一层网络的激励（假设我们只有一个样本，输入是x1,x2,输出是y）；

​ 第一层是输入，激励就是样本的特征值；记为:

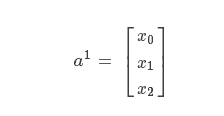
​ x0是偏置项，为1.

​ 第二层是隐藏层，激励通过特征值与区中相乘得到，然后取sigmoid函数变换，得到，未变换之前的记为：

在上面，我们最后加上了偏置项；

​ 接下来第三层是输出层：

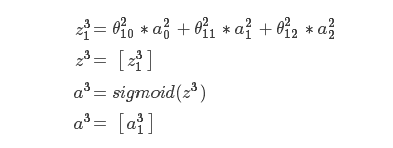
​ 因为是输出层了，所以不需要再往下计算，所以不加偏置项；

​ 上面的计算流程，从输入到输出，我们也称为前向传播(Forward propagation)。

​ 然后，我们根据损失函数，写出损失函数的公式，在这里，只有一个输入，一个输出，所以损失函数写出来较为简单：

​ 在这里，m=1;

​ 说明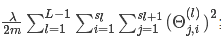：实际上就是所有的权重的平方和，一般不会将和偏置项相乘的那个放进来；这个项很简单，暂时先不管它，后面不暂时不写这一项（这个是正则化）。

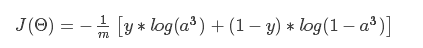
​ 然后我们得到了上面的式子，这里我们知道，如果我们想要求θ212的偏导数的话，会发现，这个式子其实是一个复合函数，y是常数，a3是z3的sigmoid函数变换，而z3则是a2与权重相乘得来的，现在我们找到了权重在哪里，就可以开始求偏导了，在这里，a3写成s(z3)，然后，我们就得到了下面的推导：

 

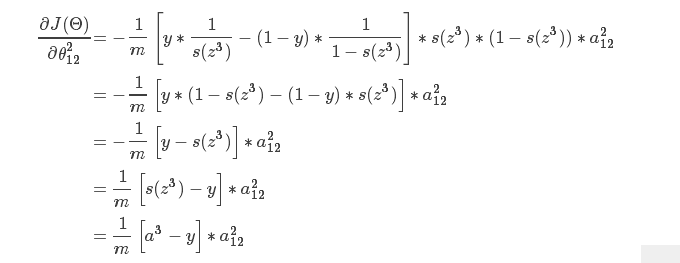
​ 根据上面的推导，可以得到下面的式子：

​ 所以，还记得前面所说的，我盟从上往下求导，保存当前对多个子单元的偏导数，根据上面的式子，我们知道，对于第二个权重矩阵的偏导，可以由[a3−y]乘以前一层网络的激励，然后除以样本个数来得到，因此有时候我们会将这个差值称为δ3，保存下来，使用矩阵的形式相乘，得到第二个权重矩阵的偏导数；

​ 现在我们已经得到了第二个权重矩阵的偏导数，如何求第一个权重矩阵中的偏导数呢？

​ 比如说，我们现在要对θ112求偏导：

​ 从上线的式子，我们就可以看出来，我们保存的导数可以直接乘，如果而不用再次计算一遍，如果有多层网络，实际上后面的过程与这个是一样的，所以就得到了这样的式子：

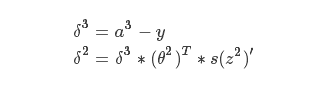
​ 因为这个网络就是3层，所以这样就可以得出全部的偏导数，如果是多层，原理是一样的，不断地乘下去，从第二个式子开始，后面的形式都是一样的。