[POJ 1003] Hangover C++解题

 

 

Hangover

Time Limit: 1000MS		Memory Limit: 10000K
Total Submissions: 95164		Accepted: 46128

Description

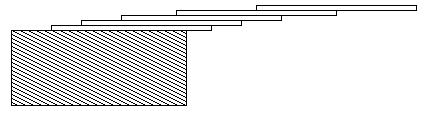
How far can you make a stack of cards overhang a table? If you have one card, you can create a maximum overhang of half a card length. (We're assuming that the cards must be perpendicular to the table.) With two cards you can make the top card overhang the bottom one by half a card length, and the bottom one overhang the table by a third of a card length, for a total maximum overhang of 1/2 + 1/3 = 5/6 card lengths. In general you can make n cards overhang by 1/2 + 1/3 + 1/4 + ... + 1/(n + 1) card lengths, where the top card overhangs the second by 1/2, the second overhangs tha third by 1/3, the third overhangs the fourth by 1/4, etc., and the bottom card overhangs the table by 1/(n + 1). This is illustrated in the figure below.

Input

The
input consists of one or more test cases, followed by a line containing
the number 0.00 that signals the end of the input. Each test case is a
single line containing a positive floating-point number c whose value is
at least 0.01 and at most 5.20; c will contain exactly three digits.

Output

For
each test case, output the minimum number of cards necessary to achieve
an overhang of at least c card lengths. Use the exact output format
shown in the examples.

Sample Input

1.00
3.71
0.04
5.19
0.00

Sample Output

3 card(s)
61 card(s)
1 card(s)
273 card(s)

翻译：

翻译：

　　若将一叠卡片放在一张桌子的边缘，你能放多远？如果你有一张卡片，你最远能达到卡片长度的一半。（我们假定卡片都正放在桌 子上。）如果你有两张卡片，你能使最上的一张卡片覆盖下面那张的1/2，底下的那张可以伸出桌面1/3的长度，即最远能达到 1/2 + 1/3 = 5/6 的卡片长度。一般地，如果你有n张卡片，你可以伸出 1/2 + 1/3 + 1/4 + ... + 1/(n + 1) 的卡片长度，也就是最上的一张卡片覆盖第二张1/2，第二张超出第三张1/3，第三张超出第四张1/4，依此类推，最底的一张卡片超出桌面1/(n + 1)。下面有个图形的例子：

　　

　　现在给定伸出长度C（0.00至5.20之间），输出至少需要多少张卡片。

解决思路

这是一道水题，直接按照要求模拟就可以了。

源码

 /*
 poj 1000
 version:1.0
 author:Knight
 Email:S.Knight.Work@gmail.com
 */

 #include<cstdio>
 using namespace std;
 int main(void)
 {
     double c;
     int i;
     double Overhangs;
     while(scanf("%lf", &c) == )
     {
         if (0.0 == c)
         {
             return ;
         }
         Overhangs = ;
         for (i=; i; i++)
         {
             Overhangs += 1.0 / (i + );
             if (Overhangs >= c)
             {
                 break;
             }
         }
         printf("%d card(s)\n", i);
     }
     return ;
 }