二叉树遍历入门 Lebal：research

解决二叉树遍历的画法

对于二叉树的基本概念，一般学生都知道，但对于二叉树的遍历，在实际运用中可以发现很多问题，这里提供一次性彻底解决这个问题的方法。

二叉树的遍历

二叉树的遍历是指不重复地访问二叉树中的所有结点。

由于二叉树是一种非线性结构，因此，对二叉树的遍历要比遍历线性表复杂得多。在遍历二叉树的过程中，当访问到某个结点时，再往下访问可能有两个分支，那么先访问哪一个分支呢?

对于二叉树来说，需要访问根结点、左子树上的所有结点、右子树上的所有结点，在这三者中，究竟先访问哪一个?也就是说，遍历二叉树的方法实际上是要确定访问各结点的顺序，以便不重不漏地访问到二叉树中的所有结点。

在遍历二叉树的过程中，一般先遍历左子树，然后再遍历右子树。在先左后右的原则下，根据访问根结点的次序，二叉树的遍历可以分为三种：前序遍历、中序遍历、后序遍历。这三种说法实际是指对根结点的访问顺序决定的，下面分别介绍这三种遍历的方法。

1．前序遍历(DLR)

所谓前序遍历是指在访问根结点、遍历左子树与遍历右子树这三者中，首先访问根结点，然后遍历左子树，最后遍历右子树；并且，在遍历左、右子树时，仍然先访问根结点，然后遍历左子树，最后遍历右子树。因此，前序遍历二叉树的过程是一个递归的过程。

下面是二叉树前序遍历的简单描述：

若二叉树为空，则结束返回。

否则：

(1)访问根结点；

(2)前序遍历左子树；

(3)前序遍历右子树。

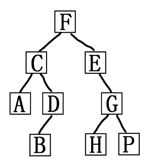
在此特别要注意的是，在遍历左右子树时仍然采用前序遍历的方法。如图所示：

二叉树进行前序遍历，则遍历的结果为F，C，A，D，B，E，G，H，P(称为该二叉树的前序序列)。

2．中序遍历(LDR)

所谓中序遍历是指在访问根结点、遍历左子树与遍历右子树这三者中，首先遍历左子树，然后访问根结点，最后遍历右子树；并且，在遍历左、右子树时，仍然先遍历左子树，然后访问根结点，最后遍历右子树。因此，中序遍历二叉树的过程也是一个递归的过程。

下面是二叉树中序遍历的简单描述：

若二叉树为空，则结束返回。

否则：

(1)中序遍历左子树；

(2)访问根结点；

(3)中序遍历左子树。

二叉树进行中序遍历，则遍历结果为A，C，B，D，F，E，H，G，P(称为该二叉树的中序序列)。
    在此也要特别注意的是，在遍历左右子树时仍然采用中序遍历的方法。如图所示：

3．后序遍历(LRD)    ．

所谓后序遍历是指在访问根结点、遍历左子树与遍历右子树这三者中，首先遍历左子树，然后遍历右子树，最后访问根结点，并且，在遍历左、右子树时，仍然先遍历左子树，然后遍历右子树，最后访问根结点。因此，后序遍历二叉树的过程也是一个递归的过程。

下面是二叉树后序遍历的简单描述：

若二叉树为空，则结束返回。否则：

(1)后序遍历左子树；

(2)后序遍历右子树；

(3)访问根结点。

在此也要特别注意的是，在遍历左右子树时仍然采用后序遍历的方法。如图所示：

二叉树进行后序遍历，则遍历结果为A，B，D，C，H，P，G，E， F。

配套练习

练习一:

某图遍历顺序如下：

先序遍历：

ABDGCEF

中序遍历：

DGBAECF

请写出该图后续遍历

-------------------------------------------我是分割线 -------------------------------------------

答案:

后序遍历：

GDBEFCA

个人方法:先写出中序投影,再根据中序投影及前序画图,最后写后序,

投影如下图:（非本例题，仅供参考）

从左往右即为中序

还有一个很好的前序解释图：