计算城市间的球面距离（C++实现）

#include<iostream>
#include<string>
#include<cmath>
#include<iomanip>

using namespace std;

struct City          //城市结构体
{
    string name;
    int EorW;//东经还是西经？东经1，西经0
    int NorS;//北纬还是南纬？北纬1，南纬0
    double lon;//经度
    double lat;//纬度
    City()
    {
        EorW = ;
        NorS = ;
    }
};

const double PI = 3.1415926;
const double R = 6371.0;//地球半径

int Iputn()   //input number输入城市数量
{
    int n;
    bool flag = true;
    while (flag)
    {
        cout << "请输入城市个数（正整数）：" << '\n';
        cin >> n;
        if ( >= n)
        {
            cout << "您的输入不符合要求！重新输入请按1，退出请按0：" << '\n';
            int choice;
            cin >> choice;
            if ( != choice){ flag = false;  }
        }
        if (flag)flag = false;
        else flag = true;
    }
    return n;
}

int ChoDir(int dir)   //choose direction  选择方向（东西经，南北纬）
{
    string str1, str2;
    if ( == dir){ str1 = "东经"; str2 = "西经"; }
    else{ str1 = "北纬"; str2 = "南纬"; }
    bool flag = true;
    int choice;
    while (flag)
    {
        cout << "请您选择"<<str1<<"还是"<<str2<<"：" <<"1." <<str1 << "；" << "0."<<str2 << '\n';
        cin >> choice;
        if (choice< || choice>)
        {
            cout << "您的输入不符合要求！重新输入请按1，退出程序请按0：" << '\n';
            int choice1;
            cin >> choice1;
            if (!= choice1)flag = false;
        }
        if (flag)flag = false;
        else flag = true;
    }
    return choice;
}

double Iputcoo(int option)  //input coordinate    输入坐标
{
    string str;
    double up;
    if ( == option){ str = "东经"; up = 180.0; }
    else if ( == option){ str = "西经"; up = 180.0; }
    else if ( == option){ str = "北纬"; up = 90.0; }
    else { str = "南纬"; up = 90.0; }
    double coor;
    bool flag = true;
    while (flag)
    {
        cout << "请您输入" << str << "（0到"<<up<<"间的有理数）：" << '\n';
        cin >> coor;
        if (coor<0.0||coor>up)
        {
            cout << "您的输入不符合要求，重新输入请按1，退出请按0：" << '\n';
            int choise;
            cin >> choise;
            if ( != choise)flag = false;
        }
        if (flag)flag = false;
        else flag = true;
    }
    return coor;
}

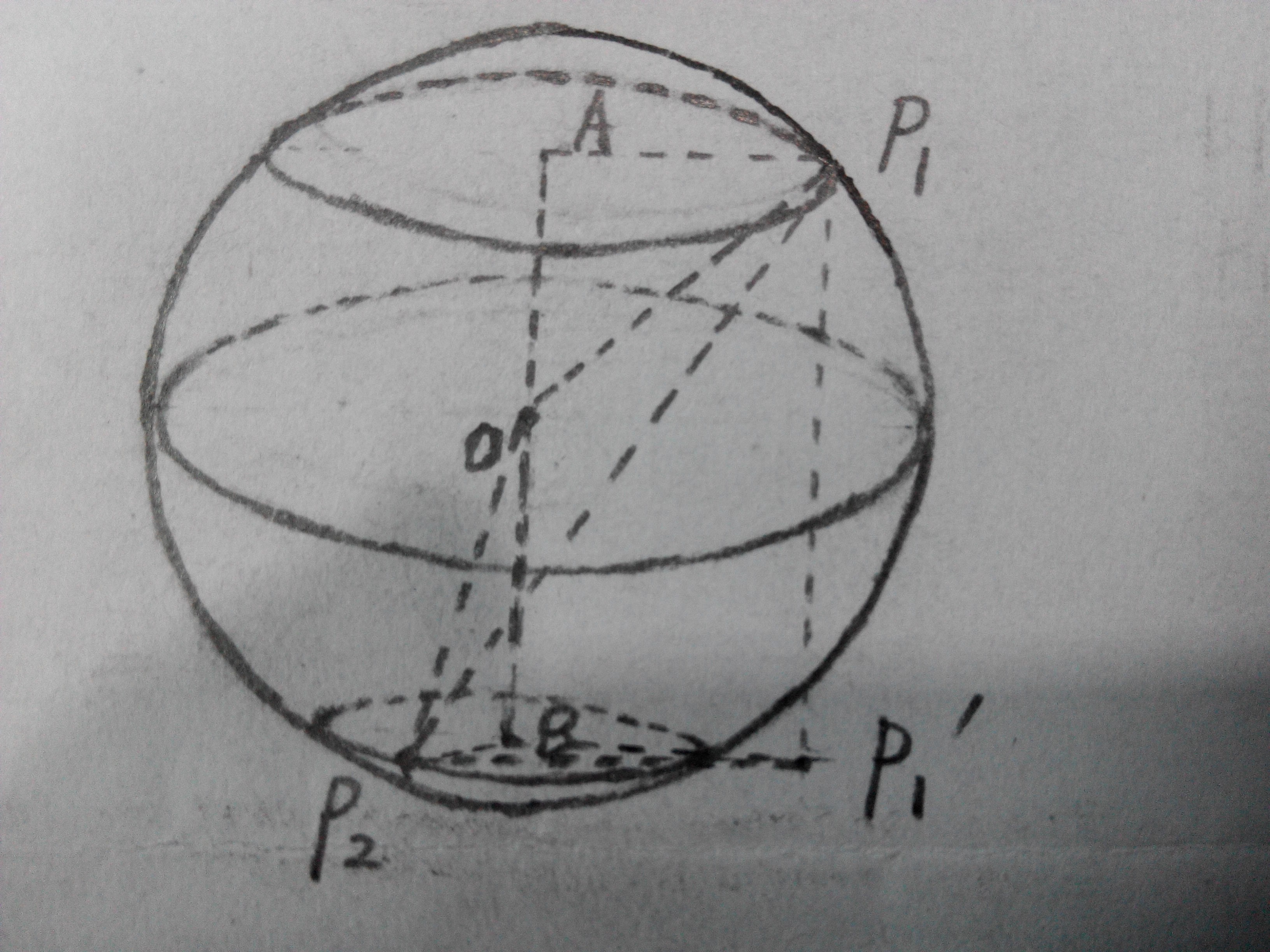
double Calcu(City& P1, City& P2)      //calculate 计算两点加球面距
{
    if (P1.name == P2.name)return 0.0;
    //求AB
    double AB;
    double OA = sin(P1.lat); double OB = sin(P2.lat);
    if (P1.NorS == P2.NorS) AB = fabs(OA - OB);
    else AB = OA + OB;
    //求夹角
    double angle;
    if (P1.EorW == P2.EorW)  angle = fabs(P1.lon - P2.lon);
    else angle = P1.lon + P2.lon;
    //求P1A、P2B
    double P1A = cos(P1.lat); double P2B = cos(P2.lat);
    //求_P1P2_2   （P1'P2的平方）
    double _P1P2_2 = P1A*P1A + P2B*P2B -  * cos(angle)*P1A*P2B;
    //求P1P2_2   （P1P2的平方）
    double P1P2_2 = _P1P2_2 + AB*AB;
    //求夹角1   （OP1与OP2间的夹角）
    double angle1 = acos(( - P1P2_2) / 2.0);
    //求球面距
    return R*angle1;
}

int main()
{
    int num = Iputn();                //输入城市数量
    if ( >= num){ exit(); }
    struct City* city = new City[num];//创建数组
    for (int i = ; i < num; i++)
    {
        getchar();                               //输入城市名称
        cout << "请您输入城市" << i +  << "的名称：" << '\n';
        getline(cin, city[i].name);
        int choice = ChoDir();                  //输入东西经
        if (choice< || choice>){ delete[] city; exit(); }
        if ( == choice)
        {
            double elon = Iputcoo();
            if (elon<0.0|| elon>180.0)
            {
                delete[] city;
                exit();
            }
            city[i].lon = PI*elon / 180.0;     //角度转弧度
            city[i].EorW = ;      //东经
        }
        else
        {
            double wlon = Iputcoo();
            if (wlon<0.0 || wlon>180.0)
            {
                delete[] city;
                exit();
            }
            city[i].lon = PI*wlon / 180.0;
            city[i].EorW = ;      //西经
        }
        choice = ChoDir();                  //输入南北纬
        if (choice< || choice>){  delete[] city; exit(); }
        if ( == choice)
        {
            double nlat = Iputcoo();
            if (nlat<0.0 || nlat>90.0)
            {
                delete[] city;
                exit();
            }
            city[i].lat = PI*nlat / 180.0;
            city[i].NorS = ;      //北纬
        }
        else
        {
            double slat = Iputcoo();
            if (slat<0.0 || slat>90.0)
            {
                delete[] city;
                exit();
            }
            city[i].lat = PI*slat / 180.0;
            city[i].NorS = ;        //南纬
        }
    }
    cout << "Start\\End   ";
    for (int i = ; i < num; i++)
        cout << setw()<<setiosflags(ios::left)<<city[i].name;
    cout << '\n';
    for (int i = ; i < num; i++)
    {
        cout << setw()<<setiosflags(ios::left)<<city[i].name;
        for (int j = ; j < num; j++)
            cout << setw() << setiosflags(ios::fixed) << setprecision() << Calcu(city[i], city[j]);
        cout << '\n';
    }
    delete[] city;//delete掉new的数组
    return ;
}