雷达无线电系列（一）几种常见的幅度分布函数（matlab）

文件下载地址：

https://github.com/mufasa007/myblog/tree/master/%E9%9B%B7%E8%BE%BE%E6%97%A0%E7%BA%BF%E7%94%B5%E7%B3%BB%E5%88%97%EF%BC%88%E4%B8%80%EF%BC%89%E5%87%A0%E7%A7%8D%E5%B8%B8%E8%A7%81%E7%9A%84%E5%B9%85%E5%BA%A6%E5%88%86%E5%B8%83%E5%87%BD%E6%95%B0%EF%BC%88matlab%EF%BC%89

一，瑞利幅度分布模型

　　① 常规模型

  

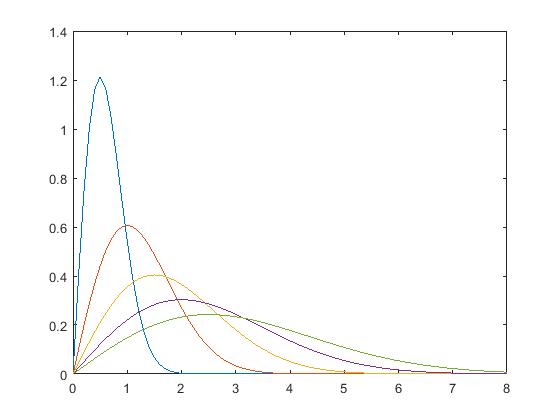
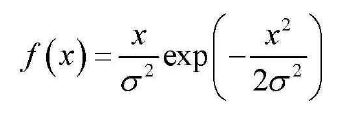
function [fx, Fx, Exn, Ex] = pdf_rayleigh(x, sigma, n)
fx = x./(sigma.^2).*exp(-1.*x.^2./(2.*sigma.^2));
Fx = 1 - exp(-x.^2/(2.*sigma.^2));
Exn = 2.^(n./2).*sigma.^2.*gamma(1+n./2);
Ex = sqrt(pi/(2.*sigma));
end

　　

　　②AB模型

  

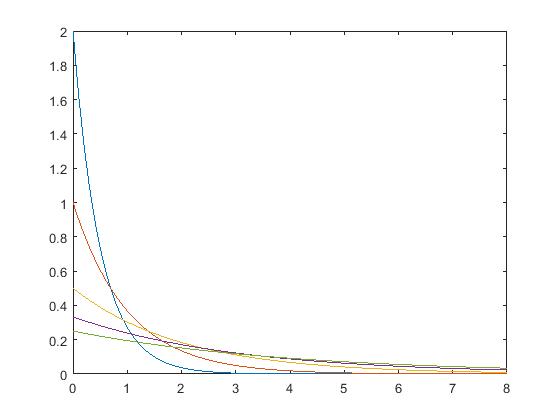
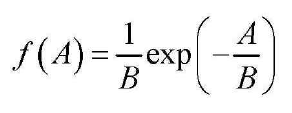
function [fA] = pdf_ABrayleigh(A, B)
fA = 1/B.*exp(-1.*(A/B));
end

　　

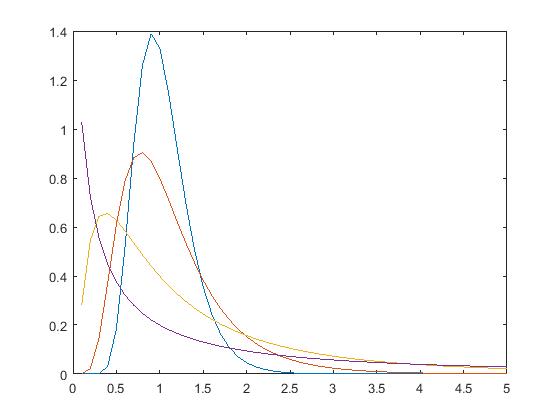
二，对数正态分布模型

   

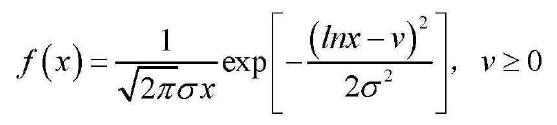
function [fx, Fx, Exn, Ex, Dx] = pdf_lognormal(x, sigma, v, n)
fx = 1./(sqrt(2.*pi).*sigma.*x).*exp(-1.*(log(x)-v).^2./(2.*sigma.^2));
Fx = 1 - exp(-((log(x)-v)/sigma).^2/(2.*sigma.^2));
Exn = exp(1/2.*(n.*sigma).^2+n.*v);
Ex = v.*exp((sigma.^2)/2);
Dx = v.^2.*exp(sigma.^2).*(exp(sigma.^2)-1);
end

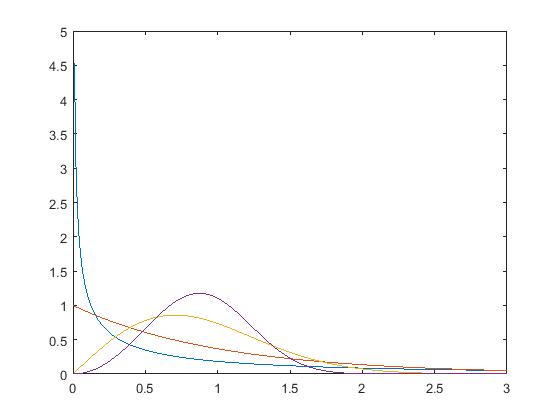
三，韦布尔幅度分布模型

 

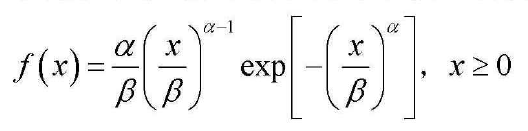
function [fx, Fx, Exn, Ex, Dx] = pdf_weibull(x, alpha, beta, n)
fx = alpha./beta.*(x./beta).^(alpha-1).*exp(-(x./beta).^alpha);
Fx = 1 - exp(-(x./beta).^alpha);
Exn = beta.^n.*gamma(n./alpha+1);
Ex = beta.*gamma(1./alpha+1);
Dx = beta.^2.*(gamma(2./alpha + 1) - gamma(1./alpha + 1).^2);
end

　

四，k分布

  

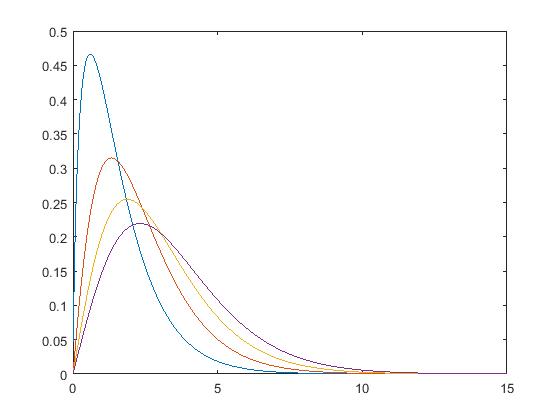
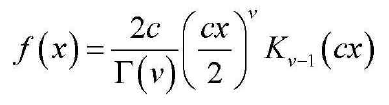
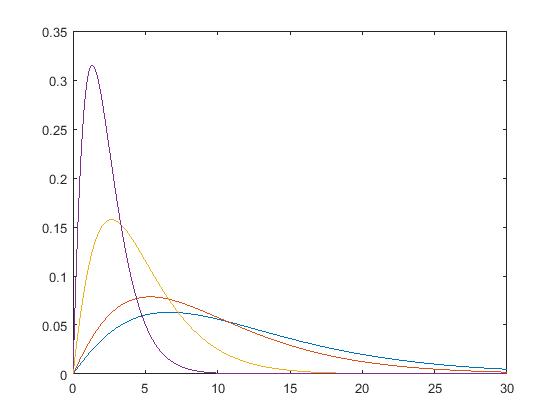
function [fx, Fx, Exn] = pdf_k(x, c, v, n)
fx = (2.*c./gamma(v)).*(c.*x./2).^v.*besselk(v-1,c.*x);
Fx = 1 - 2./gamma(v).*(c.*x./2).^v.*besselk(v,c.*x);
Exn = gamma(n./2+1).*gamma(n./2+v)./gamma(v).*(2./c).^n;
end

　　

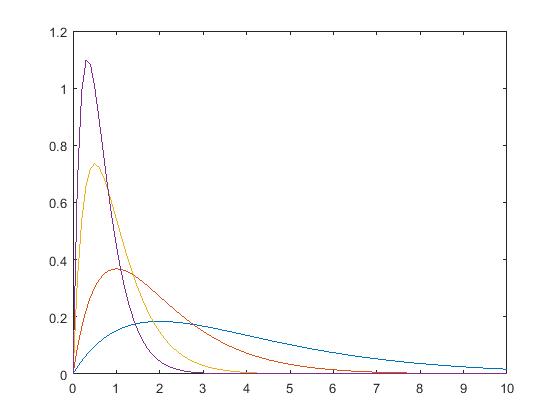
五，Gamma分布

   

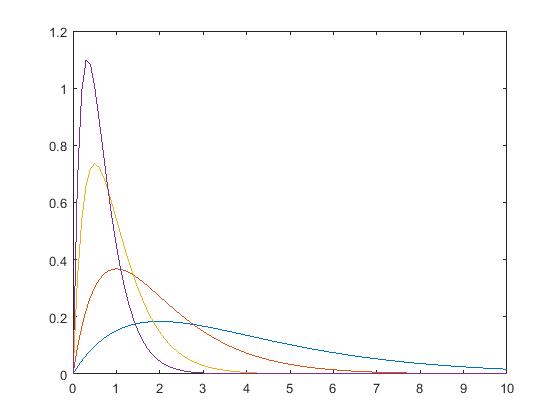
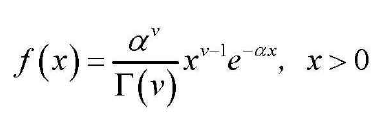
function [fx, Ex, Dx] = pdf_gamma(x, v, alpha)
fx = alpha.^v/gamma(v).*x.^(v-1).*exp(-alpha.*x);
Ex = v/alpha;
Dx = v/alpha^2;
end

　　

六，测试运行程序

clc;
%% 测试k分布v参数
% x = 0:0.01:15;
% c=1;
% n=1;
% figure;
% [fx0, Fx, Exn] = pdf_k(x, c, 1, n);
% [fx1, Fx, Exn] = pdf_k(x, c, 2, n);
% [fx2, Fx, Exn] = pdf_k(x, c, 3, n);
% [fx3, Fx, Exn] = pdf_k(x, c, 4, n);
% [fx4, Fx, Exn, Ex, Dx] = pdf_lognormal(x, 2.5, v, n);
% plot(x,fx0, x,fx1, x,fx2, x,fx3);
 
%% 测试k分布c参数
% x = 0:0.01:30;
% v=2;
% n=1;
% figure;
% [fx0, Fx, Exn] = pdf_k(x, 0.2, v, n);
% [fx1, Fx, Exn] = pdf_k(x, 0.25, v, n);
% [fx2, Fx, Exn] = pdf_k(x, 0.5, v, n);
% [fx3, Fx, Exn] = pdf_k(x, 1, v, n);
% % [fx4, Fx, Exn, Ex, Dx] = pdf_lognormal(x, 2.5, v, n);
% plot(x,fx0, x,fx1, x,fx2, x,fx3);
 
%% 测试韦布尔分布beta参数
% x = 0:0.01:8;
% alpha=3;
% n=1;
% figure;
% [fx0, Fx, Exn, Ex, Dx] = pdf_weibull(x, alpha, 1, n);
% [fx1, Fx, Exn, Ex, Dx] = pdf_weibull(x, alpha, 2, n);
% [fx2, Fx, Exn, Ex, Dx] = pdf_weibull(x, alpha, 3, n);
% [fx3, Fx, Exn, Ex, Dx] = pdf_weibull(x, alpha, 4, n);
% % [fx4, Fx, Exn, Ex, Dx] = pdf_lognormal(x, 2.5, v, n);
% plot(x,fx0, x,fx1, x,fx2, x,fx3);
 
%% 测试韦布尔分布alpha参数
% x = 0:0.01:3;
% beta=1;
% n=1;
% figure;
% [fx0, Fx, Exn, Ex, Dx] = pdf_weibull(x, 0.5, beta, n);
% [fx1, Fx, Exn, Ex, Dx] = pdf_weibull(x, 1, beta, n);
% [fx2, Fx, Exn, Ex, Dx] = pdf_weibull(x, 2, beta, n);
% [fx3, Fx, Exn, Ex, Dx] = pdf_weibull(x, 3, beta, n);
% % [fx4, Fx, Exn, Ex, Dx] = pdf_lognormal(x, 2.5, v, n);
% plot(x,fx0, x,fx1, x,fx2, x,fx3);
 
%% 测试对数正态v参数
% x = 0:0.1:20;
% sigma=1;
% n=1;
% figure;
% [fx0, Fx, Exn, Ex, Dx] = pdf_lognormal(x, sigma, 0.5, n);
% [fx1, Fx, Exn, Ex, Dx] = pdf_lognormal(x, sigma, 1, n);
% [fx2, Fx, Exn, Ex, Dx] = pdf_lognormal(x, sigma, 2, n);
% [fx3, Fx, Exn, Ex, Dx] = pdf_lognormal(x, sigma, 3, n);
% % [fx4, Fx, Exn, Ex, Dx] = pdf_lognormal(x, 2.5, v, n);
% plot(x,fx0, x,fx1, x,fx2, x,fx3);
 
%% 测试对数正态sigma参数
% x = 0:0.1:5;
% v=0;
% n=1;
% figure;
% [fx0, Fx, Exn, Ex, Dx] = pdf_lognormal(x, 0.3, v, n);
% [fx1, Fx, Exn, Ex, Dx] = pdf_lognormal(x, 0.5, v, n);
% [fx2, Fx, Exn, Ex, Dx] = pdf_lognormal(x, 1, v, n);
% [fx3, Fx, Exn, Ex, Dx] = pdf_lognormal(x, 2, v, n);
% % [fx4, Fx, Exn, Ex, Dx] = pdf_lognormal(x, 2.5, v, n);
% plot(x,fx0, x,fx1, x,fx2, x,fx3);
 
%% 测试rayleigh_AB分布函数
% figure;
% x=0:0.1:8;
% [fx0] = pdf_ABrayleigh(x, 0.5);
% [fx1] = pdf_ABrayleigh(x, 1);
% [fx2] = pdf_ABrayleigh(x, 2);
% [fx3] = pdf_ABrayleigh(x, 3);
% [fx4] = pdf_ABrayleigh(x, 4);
% plot(x,fx0, x,fx1, x,fx2, x,fx3, x,fx4);
 
%% 测试rayleigh分布函数
% n = 1;
% figure;
% [fx0, Ex0, Dx0] = pdf_rayleigh(x, 0.5, n);
% [fx1, Ex1, Dx1] = pdf_rayleigh(x, 1, n);
% [fx2, Ex2, Dx2] = pdf_rayleigh(x, 1.5, n);
% [fx3, Ex3, Dx3] = pdf_rayleigh(x, 2, n);
% [fx4, Ex4, Dx4] = pdf_rayleigh(x, 2.5, n);
% plot(x,fx0, x,fx1, x,fx2, x,fx3, x,fx4);
 
%% 测试gamma分布v参数
% x = 0:0.1:10;
% alpha = 1;
% figure;
% [fx0, Ex0, Dx0] = pdf_gamma(x, 0.5, alpha);
% [fx1, Ex1, Dx1] = pdf_gamma(x, 1, alpha);
% [fx2, Ex2, Dx2] = pdf_gamma(x, 2, alpha);
% [fx3, Ex3, Dx3] = pdf_gamma(x, 3, alpha);
% plot(x,fx0, x,fx1, x,fx2, x,fx3);
 
%% 测试gamma分布alpha参数
% x = 0:0.1:10;
% alpha = 1;
% figure;
% [fx0, Ex0, Dx0] = pdf_gamma(x, v, 0.5);
% [fx1, Ex1, Dx1] = pdf_gamma(x, v, 1);
% [fx2, Ex2, Dx2] = pdf_gamma(x, v, 2);
% [fx3, Ex3, Dx3] = pdf_gamma(x, v, 3);
% plot(x,fx0, x,fx1, x,fx2, x,fx3);