优化算法：AdaGrad | RMSProp | AdaDelta | Adam

0 - 引入

　　简单的梯度下降等优化算法存在一个问题：目标函数自变量的每一个元素在相同时间步都使用同一个学习率来迭代，如果存在如下图的情况（不同自变量的梯度值有较大差别时候），存在如下问题：

• 选择较小的学习率会使得梯度较大的自变量迭代过慢
• 选择较大的学习率会使得梯度较小的自变量迭代发散

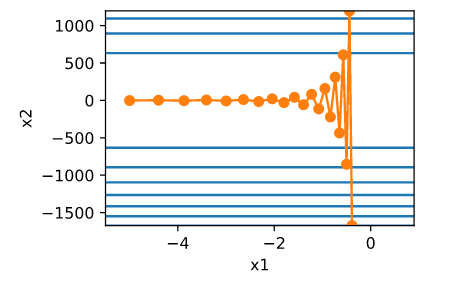　　因此，自然而然想到，要解决这一问题，不同自变量应该根据梯度的不同有不同的学习率。本篇介绍的几种优化算法都是基于这个思想的。

1 - AdaGrad算法

　　使用一个小批量随机梯度$g_t$按元素平方的累加变量$s_t$，在时间步0，AdaGrad将$s_0$中每个元素初始化为0，其更新公式为：

$$s_t\leftarrow s_{t-1}+g_t\odot g_t$$

$$x_t\leftarrow x_{t-1}-\frac{\eta}{\sqrt{s_t+\epsilon}}\odot g_t$$

　　其中$\odot$是按元素相乘，$\eta$是学习率，$\epsilon$是为了维持数值稳定性而添加的常数（如$10^{-6}$）。

2 - RMSProp算法

　　由于AdaGrad算法的机制，导致每个元素的学习率在迭代过程中只能降低或者不变，因此很可能出现早期迭代到不好的极值点之后，由于学习率太小而无法冲出这个极值点导致最后收敛到的解不优，为了解决这一问题，RMSProp是基于AdaGrad算法做了一点小修改，其更新公式为：

$$s_t\leftarrow \gamma s_{t-1}+(1-\gamma)g_t\odot g_t$$

$$x_t\leftarrow x_{t-1}-\frac{\eta}{\sqrt{s_t+\epsilon}}\odot g_t$$

　　其中，$\eta$是学习率，$\epsilon$是为了维持数值稳定性而添加的常数（如$10^{-6}$）。另外，比AdaGrad多了超参数$\gamma\in [0, 1)$，$s_t$可以看作是最近$\frac{1}{(1-\gamma)}$个时间步的小批量随机梯度平方项的加权平均，从而使得每个元素的学习率在迭代过程中不再一直降低或者不变。具体可以理解为：

• 如果最近的时间步梯度平方加权累积较小，说明梯度较小，那么学习率会增加
• 如果最近的时间步梯度平方加权累计较大，说明梯度较大，那么学习率会减小

　　有了如上机制，可以使得收敛稳定的同时，有一定几率冲出不优解，而使得最后收敛结果和开始的迭代表现相关性降低。

3 - AdaDelta算法

　　AdaDelta算法和RMSProp算法一样，使用小批量随机梯度$g_t$按元素平方的指数加权移动平均变量$s_t$，在时间步为0时，所有元素被初始化为0，其更新公式为：

$$s_t\leftarrow \rho s_{t-1}+(1-\rho)g_t\odot g_t$$

$$g_{t}^{'} \leftarrow \sqrt{\frac{\Delta x_{t-1}+\epsilon }{s_t+\epsilon}}\odot g_t$$

$$x_t\leftarrow t_{t-1}-g_{t}^{'}$$

$$\Delta x_t\leftarrow \rho \Delta x_{t-1} + (1-\rho)g_{t}^{'}\odot g_{t}^{'}$$

　　其中，$\epsilon$是为了维持数值稳定性而添加的常数（如$10^{-5}$）。另外，AdaDelta算法没有学习率这个超参，而是通过$\Delta x_t$来记录自变量变化量$g_t^'$按元素平方的指数加权移动平均，如果不考虑$\epsilon$的影响，AdaDelta算法跟RMSProp算法的不同之处在于使用$\sqrt{\Delta x_{t-1}}$来替代学习率$\eta$。

4 - Adam算法

　　Adam算法使用了动量变量$v_t$和RMSProp算法中小批量随机梯度按元素平方的指数加权移动平均变量$s_t$，并在时间步0将它们中的每个元素初始化为0。其更新公式为：

$$v_t\leftarrow \beta_1 v_{t-1} + (1-\beta_1)g_t$$

$$s_t\leftarrow \beta_2 s_{t-1} + (1-\beta_2)g_t \odot g_t$$

$$\hat{v_t}\leftarrow \frac{v_t}{1-\beta^t_1}$$

$$\hat{s_t}\leftarrow \frac{s_t}{1-\beta^t_2}$$

$$g_t^{'}\leftarrow \frac{\eta \hat{v_t}}{\sqrt{\hat{s_t}}+\epsilon}$$

$$x_t\leftarrow x_{t-1}-g_t^{'}$$

　　其中，$\eta$是学习率，$\epsilon$是为了维持数值稳定性而添加的常数（如$10^{-8}$），超参数$\beta_1\in [0, 1)$建议设为0.9，超参数$\beta_2\in [0, 1)$建议设为0.999。

5 - 总结

　　综上分析，可以得出如下几个结论：

• AdaGrad、RMSProp、AdaDelta和Adam几个优化算法，目标函数自变量中每个元素都分别拥有自己的学习率；
• AdaGrad目标函数自变量中各个元素的学习率只能保持下降或者不变，因此当学习率在迭代早期降得较快且当前解依然不佳时，由于后期学习率过小，可能较难找到一个有用的解；
• RMSProp和AdaDelta算法都是解决AdaGrad上述缺点的改进版本，本质思想都是利用最近的时间步的小批量随机梯度平方项的加权平均来降低学习率，从而使得学习率不是单调递减的（当最近梯度都较小的时候能够变大）。不同的是，RMSProp算法还是保留了传统的学习率超参数，可以显式指定。而AdaDelta算法没有显式的学习率超参数，而是通过$\Delta x$做运算来间接代替学习率；
• Adam算法可以看成是RMSProp算法和动量法的结合。

6 - 参考资料

http://zh.d2l.ai/chapter_optimization/adagrad.html

http://zh.d2l.ai/chapter_optimization/rmsprop.html

http://zh.d2l.ai/chapter_optimization/adadelta.html

http://zh.d2l.ai/chapter_optimization/adam.html