支持向量机SVM原理_python sklearn建模乳腺癌细胞分类器（推荐AAA）

python机器学习-乳腺癌细胞挖掘（博主亲自录制视频）

https://study.163.com/course/introduction.htm?courseId=1005269003&utm_campaign=commission&utm_source=cp-400000000398149&utm_medium=share

支持向量机python代码和博客介绍

https://github.com/adashofdata/muffin-cupcake

YouTube介绍

https://www.youtube.com/watch?v=N1vOgolbjSc

这是线性支持向量机，LSVM

margin

margin值越大越好，因为margin值越大，空间区分两组数据效果越好，margin值越小，空间区分两组数据效果越差

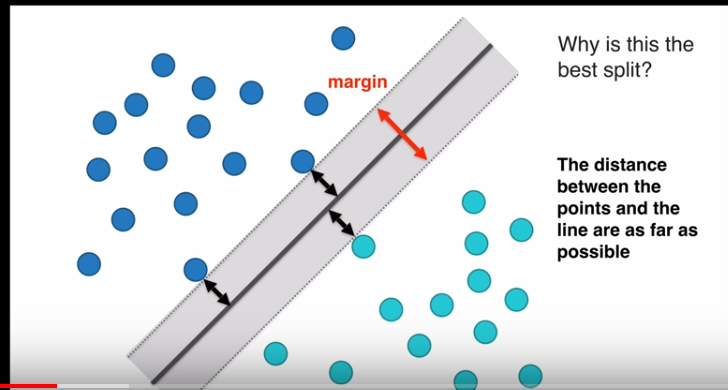
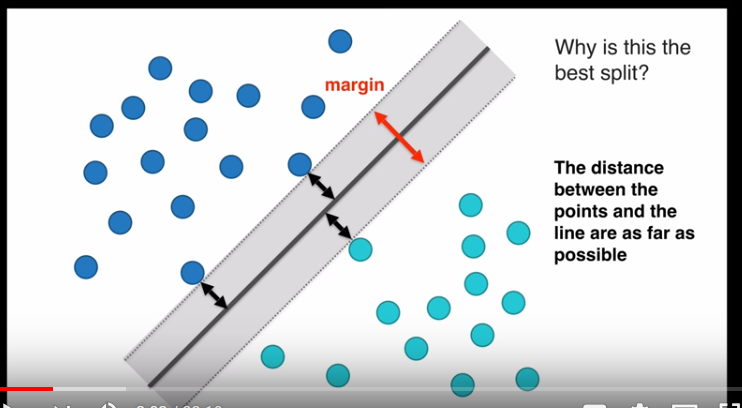
margin值最大的向量空间最好

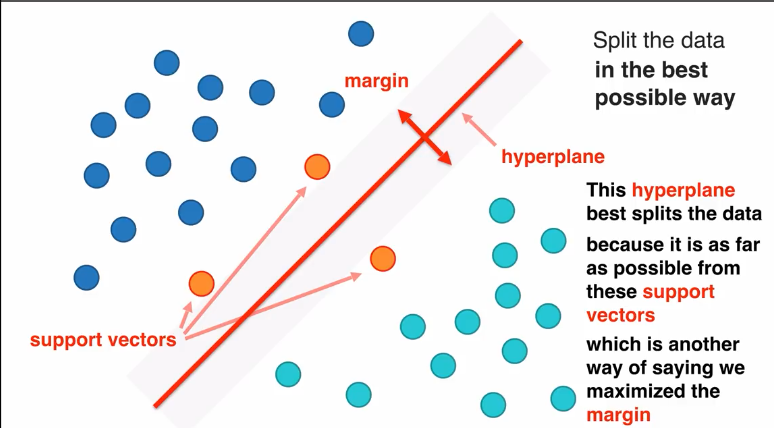
lagrange multipliers拉格朗日乘数法是解决支持向量机margin最大值方法

在数学最优问题中，拉格朗日乘数法（以数学家约瑟夫·路易斯·拉格朗日命名）是一种寻找变量受一个或多个条件所限制的多元函数的极值的方法。这种方法将一个有n 个变量与k 个约束条件的最优化问题转换为一个有n + k个变量的方程组的极值问题，其变量不受任何约束。这种方法引入了一种新的标量未知数，即拉格朗日乘数：约束方程的梯度（gradient）的线性组合里每个向量的系数。 ^[1]  此方法的证明牵涉到偏微分，全微分或链法，从而找到能让设出的隐函数的微分为零的未知数的值。

支持向量优点

1.支持多维空间

2.不同核函数用于不同决策函数

支持多维空间

非线性SVM可以转换为多维空间支持向量机

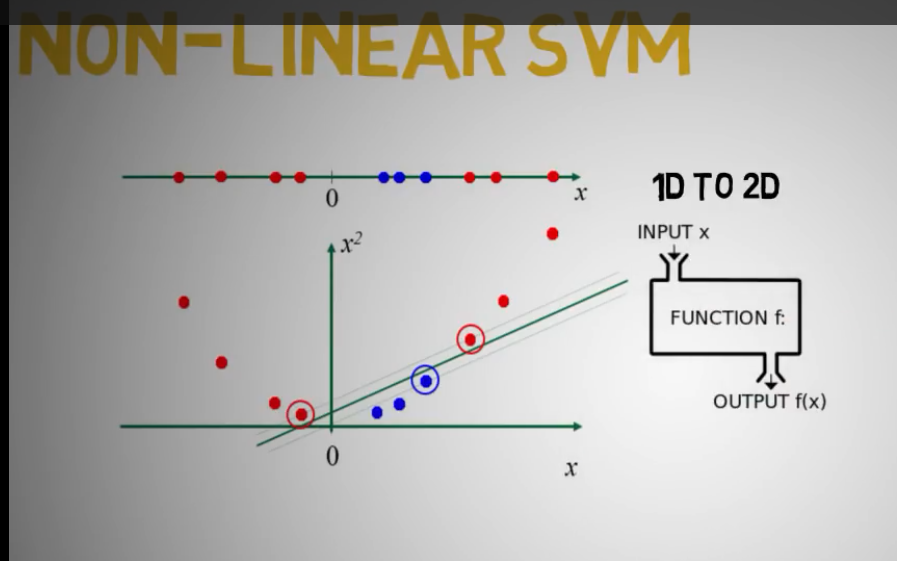
支持向量缺点：

1.如果数据特征（维度）大于样本量，支持向量机表现很差

2.支持向量机不提供概率区间估计

优点：可处理多维度数据分类，小样本数据可以工作

缺点：找到准确的核函数和C参数，gamma参数需要很大计算量

优点：灵活，处理低维度和高维度数据，高维度数据小样本量表现良好

缺点：高维度，大样本表现较差，需要数据预处理和调参

很难监控和可视化

另外推荐算法：决策树和随机森林（方便可视化，监控，容易理解）

通过核函数，非线性空间可以转换为线性空间

支持向量应用积极广泛

python脚本应用

区分两种蛋糕，根据奶油和糖两种成分，首先数据可视化

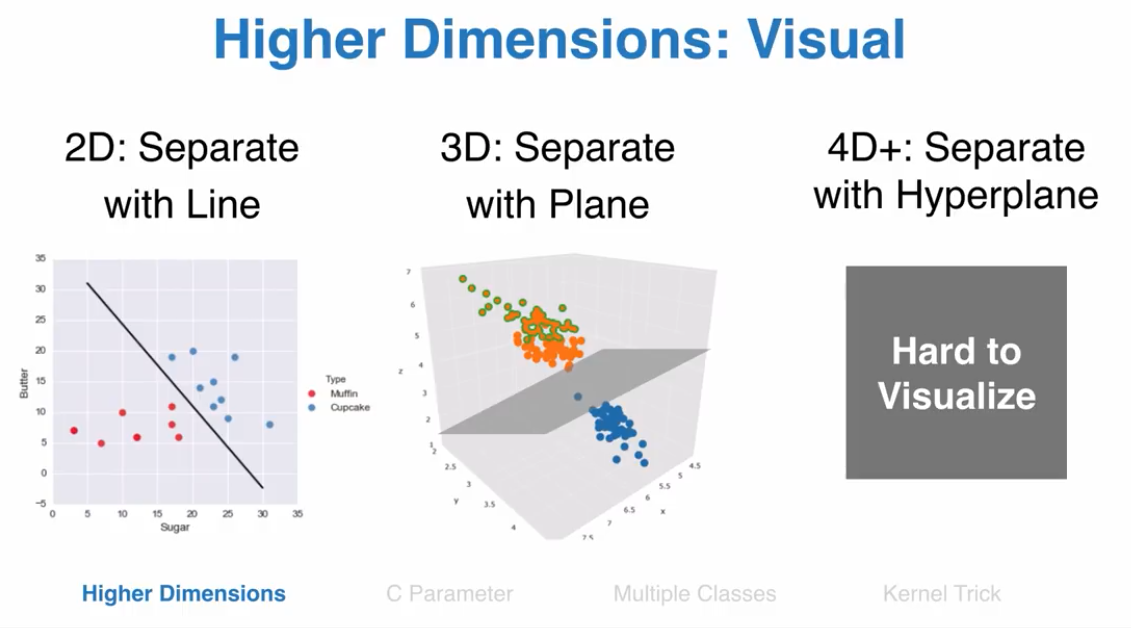
C 参数

C参数表示，你惩罚错误分类点的力度

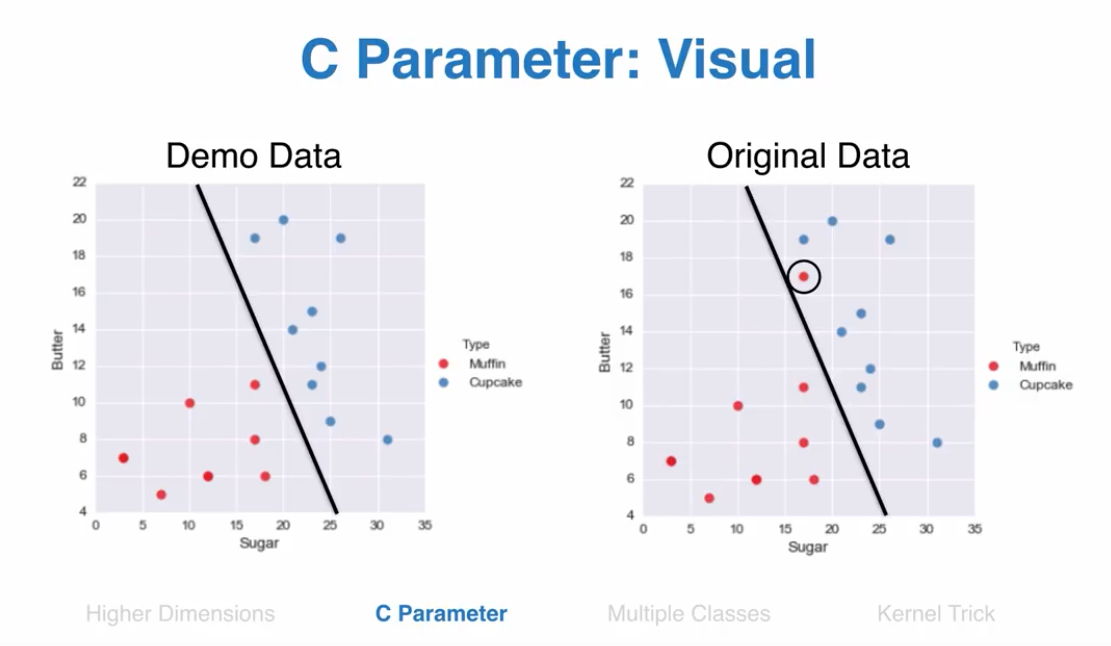
sklearn默认C参数是1

C参数设置小，算法复杂度小，C参数高，追求错误率最低

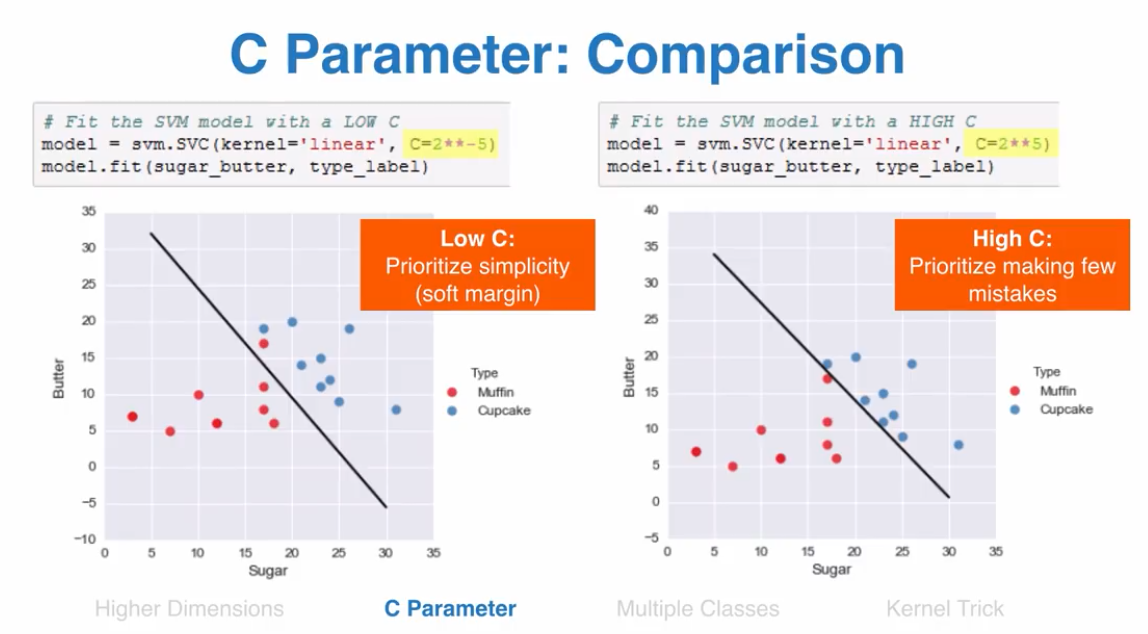
支持多个分层

python代码实现分多类，decision_function_shape="ovr"

核函数

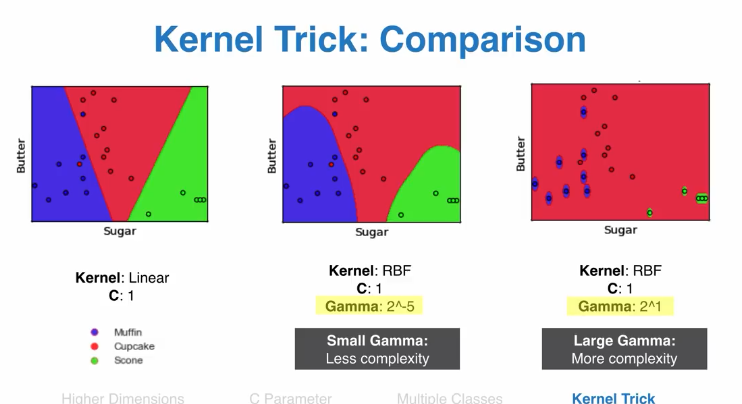
通过核函数，二维数据难以分类的可以转换为多维函数，然后分类

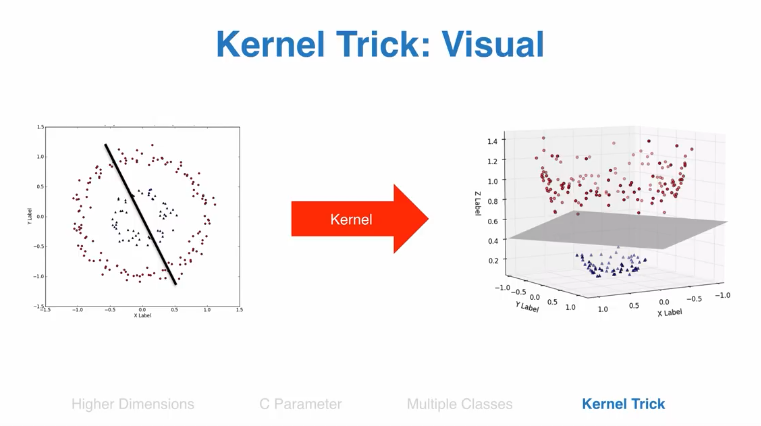
python代码kernel函数设置

gamma越高，复杂度越高

其它机器学习分类算法

 

decision_function

SVM分割超平面的绘制与SVC.decision_function( )的功能

https://blog.csdn.net/qq_33039859/article/details/69810788?locationNum=3&fps=1

在李航老师的《统计学习方法》— 支持向量机那章有个例题： 
样本点x1=(3,3),x2=(4,3),x3=(1,1),labels=(1,1,−1)x1=(3,3),x2=(4,3),x3=(1,1),labels=(1,1,−1),求分割超平面？

• 先说decision_function()的功能：计算样本点到分割超平面的函数距离。 
  • 没错，是函数距离（将几何距离，进行了归一化，具体看书）
  • 将x1=(3,3),x2=(4,3),x3=(1,1),labels=(1,1,−1)x1=(3,3),x2=(4,3),x3=(1,1),labels=(1,1,−1)带入决策函数decision_function( )，也就是分割超平面12x1+12x2−212x1+12x2−2即可得到函数距离：1, 1.5, -1,其中1 和 -1 刚好在margin边缘上，x1,x3x1,x3也就是支持向量。

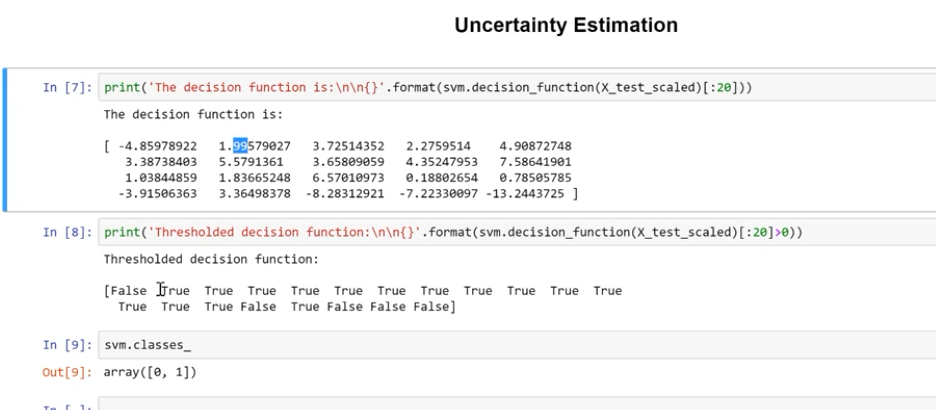
decision_function()的功能：计算样本点到分割超平面的函数距离,分割超平面一边数据是正数，一边是负数，如果是二分类，正数代表一类，负数代表另一类

乳腺癌python脚本

此脚本包括参数设置，自动调优，数据规范化，概率计算，分类预测等等

# -*- coding: utf-8 -*-
"""
Created on Fri Mar 30 21:57:29 2018

@author: Toby
项目合作联系QQ：231469242
"""
#标准化数据
from sklearn import preprocessing
from sklearn.svm import SVC
from sklearn.datasets import load_breast_cancer
from sklearn.model_selection import train_test_split
import matplotlib.pyplot as plt

cancer=load_breast_cancer()
data=cancer.data
featureNames=cancer.feature_names
#random_state 相当于随机数种子
X_train,x_test,y_train,y_test=train_test_split(cancer.data,cancer.target,stratify=cancer.target,random_state=42)
svm=SVC()
svm.fit(X_train,y_train)
print("accuracy on the training subset:{:.3f}".format(svm.score(X_train,y_train)))
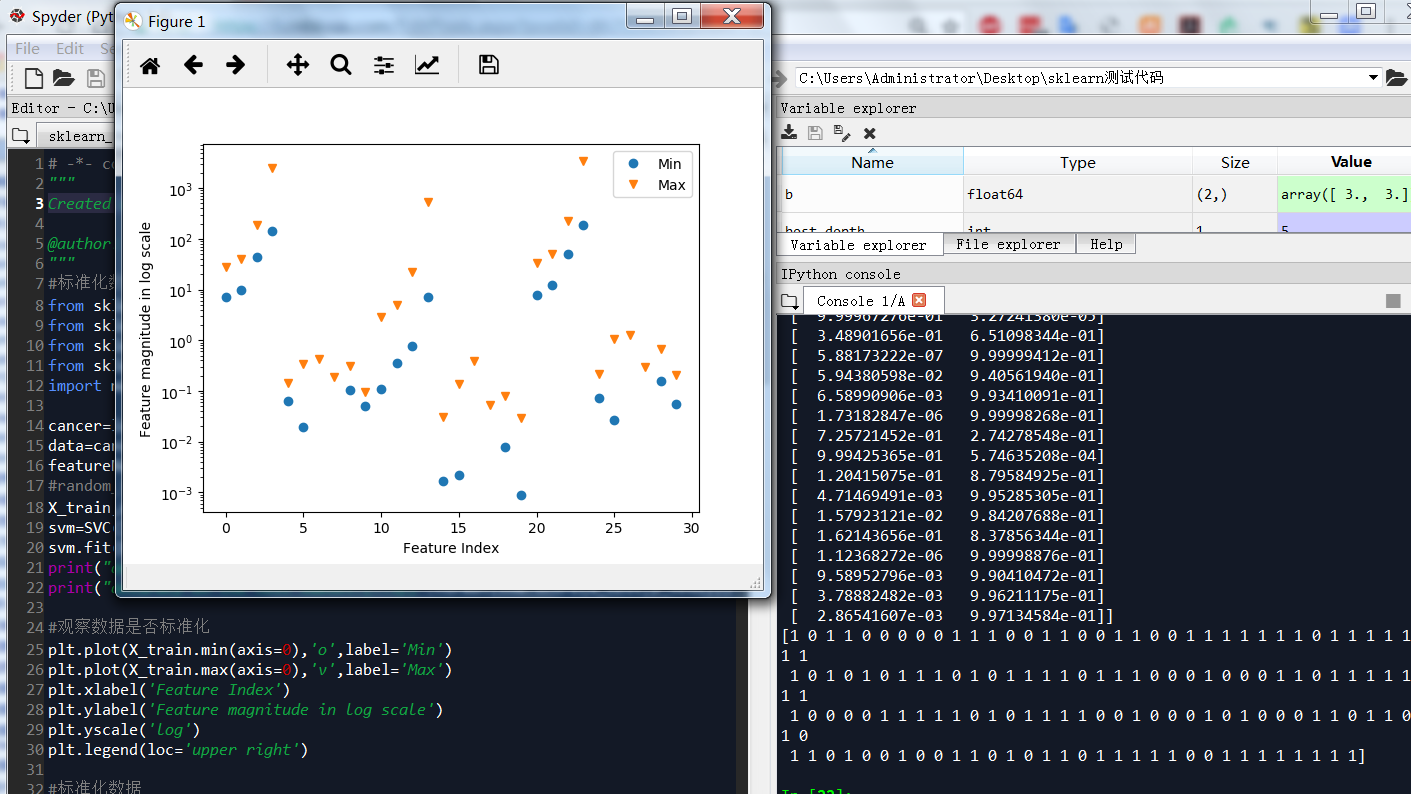
print("accuracy on the test subset:{:.3f}".format(svm.score(x_test,y_test)))

#观察数据是否标准化
plt.plot(X_train.min(axis=0),'o',label='Min')
plt.plot(X_train.max(axis=0),'v',label='Max')
plt.xlabel('Feature Index')
plt.ylabel('Feature magnitude in log scale')
plt.yscale('log')
plt.legend(loc='upper right')

#标准化数据
X_train_scaled = preprocessing.scale(X_train)
x_test_scaled = preprocessing.scale(x_test)
svm1=SVC()
svm1.fit(X_train_scaled,y_train)
print("accuracy on the scaled training subset:{:.3f}".format(svm1.score(X_train_scaled,y_train)))
print("accuracy on the scaled test subset:{:.3f}".format(svm1.score(x_test_scaled,y_test)))

#改变C参数，调优,kernel表示核函数，用于平面转换，probability表示是否需要计算概率
svm2=SVC(C=10,gamma="auto",kernel='rbf',probability=True)
svm2.fit(X_train_scaled,y_train)
print("after c parameter=10,accuracy on the scaled training subset:{:.3f}".format(svm2.score(X_train_scaled,y_train)))
print("after c parameter=10,accuracy on the scaled test subset:{:.3f}".format(svm2.score(x_test_scaled,y_test)))
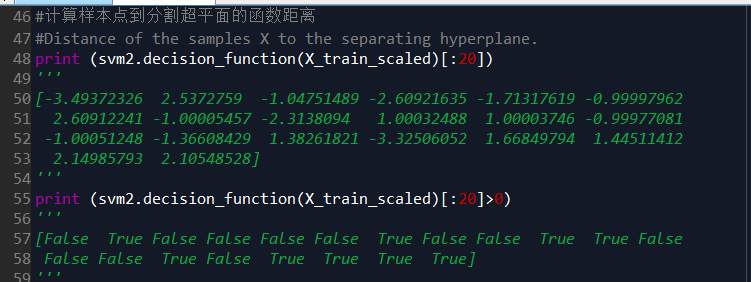
#计算样本点到分割超平面的函数距离
print (svm2.decision_function(X_train_scaled))

print (svm2.decision_function(X_train_scaled)[:20]>0)
#支持向量机分类
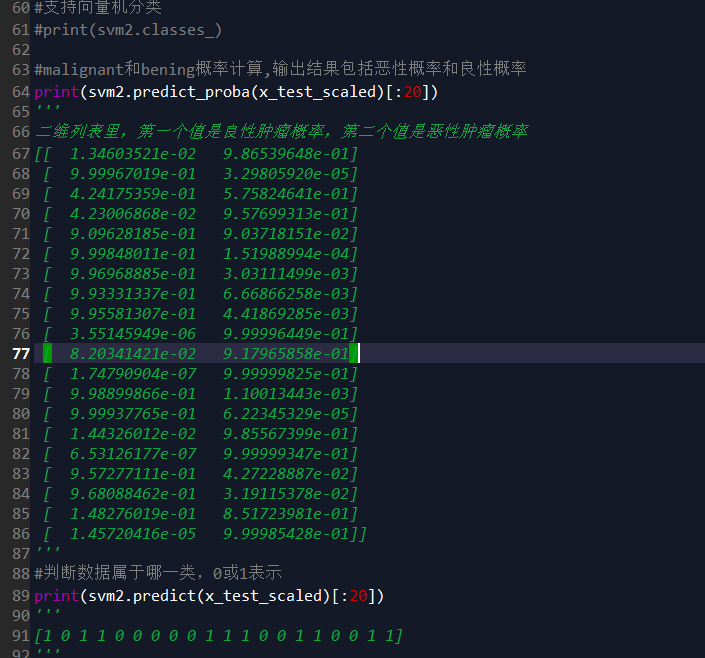
print(svm2.classes_)

#malignant和bening概率计算,输出结果包括恶性概率和良性概率
print(svm2.predict_proba(x_test_scaled))
#判断数据属于哪一类，0或1表示
print(svm2.predict(x_test_scaled))

　　

机器分类是如何抉择的？

机器决策有两种方式，第一种依靠decision_function，计算点到分割超平面距离。如果距离绝对值比较明显，说明超平面分割效果较好。

decision_function是计算点到分割超平面距离的函数,

点到平面距离大于0的属于一类，<0的属于一类

第二种方式是predict_proba是概率预测函数，概率大的值就属于对应分类

svm2.predict判断数据属于哪一类，0或1表示

 SVM分类

SVM 支持向量机，在sklearn里面，有两种，SVC支持向量分类，用于分类问题，SVR，支持向量回归，用于回归问题。

核方法

用于产生非线性分类边界。 
linear，线性核，会产生线性分类边界，一般来说它的计算效率最高，而且需要数据最少。线性函数。

from sklearn import svm
svc = svm.SVC(kernel='linear')
svc.fit(X, y)

poly，多项式核，会产生多项式分类边界。多项式函数。

svc = svm.SVC(kernel='poly',degree=4)
svc.fit(X, y)

rbf，径向基函数，也就是高斯核，是根据与每一个支持向量的距离来决定分类边界的，它能映射到无限维，是最灵活的方法，但是也需要最多的数据。容易产生过拟合问题。指数函数。

svc = svm.SVC(kernel='rbf', gamma=1e2)

多分类器 
采用”one vs one”，在任意两个样本之间设计一个SVM,k个类别的样本设计k(k-1)/2个svm，当对一个未知样本进行分类时，最后得票最多的类别即为该未知样本的类别。 
线性支持向量分类器(LinearSVC):相比于svm.SVC,使用了不同的算法，在某些数据集(比如稀疏数据集，文本挖掘)上运行得更快，对于多分类采用的就是”one vs all”的策略

svc=svm.LinearSVC(X,Y)

支持向量

就是最靠近分离边界的样本点，它们是二分类问题中最具有代表性的点。支持向量的坐标可以通过方法support_vectors_来找到。

svc.support_vectors_[:, 0], svc.support_vectors_[:, 1]

正则化

只考虑支持向量。使模型在处理样本特征的时候变得更加简单。 
正则项可以通过调整系数C来决定

#大的C值：将会有较少的支持向量，决策边界是被大多数支持向量所决定。
svc = svm.SVC(kernel='linear', C=1e3)
#小的C值：将会有较多支持向量，决策边界=类别A的平均值-类别B的平均值
svc = svm.SVC(kernel='linear', C=1e-3)

默认参数C=1，对于很多数据集，默认值就能工作的很好。 
实践经验：对许多分类器来说，对样本正则化，采用标准差正则方法是非常重要的提升预测效果的手段。

python风控评分卡建模和风控常识

https://study.163.com/course/introduction.htm?courseId=1005214003&utm_campaign=commission&utm_source=cp-400000000398149&utm_medium=share

微信扫二维码，免费学习更多python资源