machine learning 之 Neural Network 1

整理自Andrew Ng的machine learning课程week 4.

目录：

• 为什么要用神经网络
• 神经网络的模型表示 1
• 神经网络的模型表示 2
• 实例1
• 实例2
• 多分类问题

1、为什么要用神经网络

当我们有大量的features时：如$x_1, x_2,x_3.......x_{100}$

假设我们现在使用一个非线性的模型，多项式最高次为2次，那么对于非线性分类问题而言，如果使用逻辑回归的话：

$g(\theta_0+\theta_1x_1+\theta_2x_2+\theta_3x_1x_2+\theta_4x_1^2x_2+........)$

大约有5000（$\frac{n^2}{2}$）个特征，也就是说O(n²)，那么当多项式的次数为3次时，结果更加的大，O(n³)

这样多的特征带来的后果是：1.过拟合的可能性增大     2.计算的耗费很大

举个更加极端的例子，在图像问题中，每一个像素就相当于一个特征，仅对于一个50*50（已经是非常小的图片了）的图像而言，如果是灰度图像，就有2500个特征了，RGB图像则有7500个特征，对于每个特征还有255个取值；

对于这样的一个图像而言，如果用二次特征的话，就有大概3百万个特征了，如果这时候还用逻辑回归的话，计算的耗费就相当的大了

这个时候我们就需要用到neural network了。

2、神经网络的模型表示1

神经网络的基本结构如下图所示：

$x_0, x_1,x_2,x_3$是输入单元，$x_0$又被称为bias unit，你可以把bias unit都设置为1；

$\theta$是权重（或者直接说参数），连接输入和输出的权重参数；

$h_\theta(x)$是输出的结果；

对于以下的网络结构，我们有以下定义和计算公式：

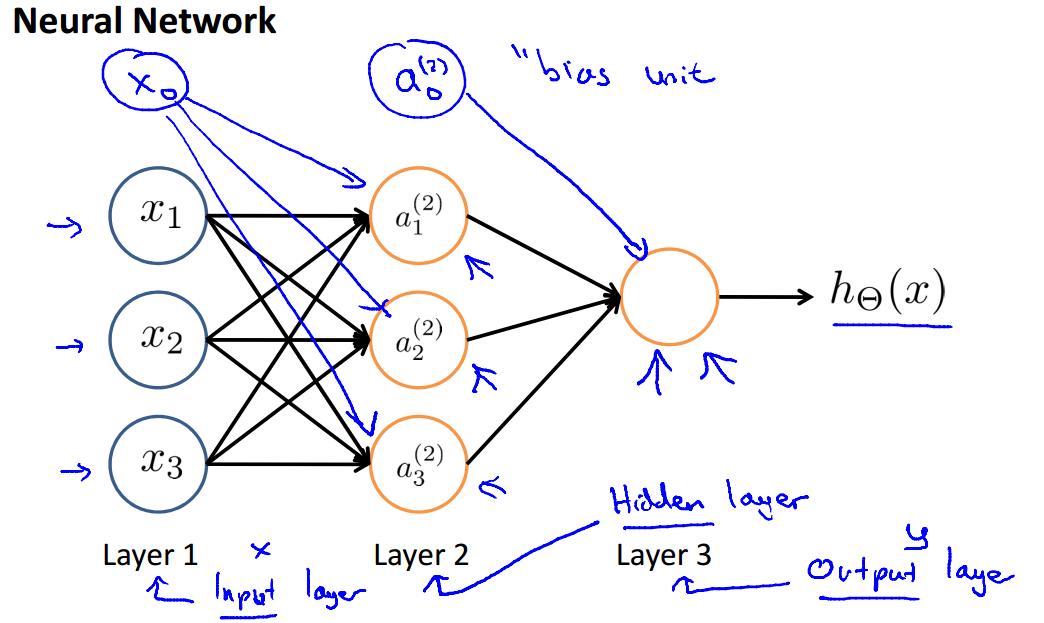
$a_i^{(j)}$：在第j层的第i个单元的activation（就是这个单元的值），中间层我们称之为hidden layers

$s_j$：第j层的单元数目

$\Theta^{(j)}$：权重矩阵，控制了从第j层到第j+1层的映射关系，$\Theta^{(j)}$的维度为$s_{j+1}*(s_j+1)$

对于$a^{(2)}$的计算公式为：

$a_1^{(2)}=g(\theta_{10}^{(1)}x_0+\theta_{11}^{(1)}x_1+\theta_{12}^{(1)}x_2+\theta_{13}^{(1)x_3})$

$a_2^{(2)}=g(\theta_{20}^{(1)}x_0+\theta_{21}^{(1)}x_1+\theta_{22}^{(1)}x_2+\theta_{23}^{(1)}x_3)$

$a_3^{(2)}=g(\theta_{30}^{(1)}x_0+\theta_{31}^{(1)}x_1+\theta_{32}^{(1)}x_2+\theta_{33}^{(1)}x_3)$

那么同理，

$h_\Theta(x)=a_1^{(3)}=g(\theta_{10}^{(2)}a_0^{(2)}+\theta_{11}^{(2)}a_1^{(2)}+\theta_{12}^{(2)}a_2^{(2)}+\theta_{13}^{(2)}a_3^{(2)})$

3、神经网络模型表示2

forward propagation: vectorized implementation

对以上的公式的向量化表示：

$z_1^{(2)}=\theta_{10}^{(1)}x_0+\theta_{11}^{(1)}x_1+\theta_{12}^{(1)}x_2+\theta_{13}^{(1)x_3}$

$a_1^{(2)}=g(z_1^{(2)})$

写成向量即为：

$ a^{(1)}=x= \begin{bmatrix} x_0 \\  x_1 \\ x_2 \\ x_3  \end{bmatrix} $          $ z^{(2)}=\begin{bmatrix} z^{(2)}_1 \\ z^{(2)}_1 \\ z^{(2)}_1 \end{bmatrix} $          $\Theta^{(1)}= \begin{bmatrix} \theta^{(1)}_{10} & \theta^{(1)}_{11} & \theta^{(1)}_{12} & \theta^{(1)}_{13} \\ \theta^{(1)}_{20} & \theta^{(1)}_{21} & \theta^{(1)}_{22} & \theta^{(1)}_{23} \\ \theta^{(1)}_{30} & \theta^{(1)}_{31} & \theta^{(1)}_{32} & \theta^{(1)}_{33} \\ \end{bmatrix}$

因此：

$z^{(2)}=\Theta^{(1)}a^{(1)}$

$a^{(2)}=g(z^{(2)})$

加上$a^{(2)}_0=1$：

$z^{(3)}=\Theta^{(2)}a^{(2)}$

$a^{(3)}=h_\Theta(x)=g(z^{(3)})$

以上即为向量化的表达方式。

对于每个$a^{(j)}$都会学习到不同的特征

4、实例1

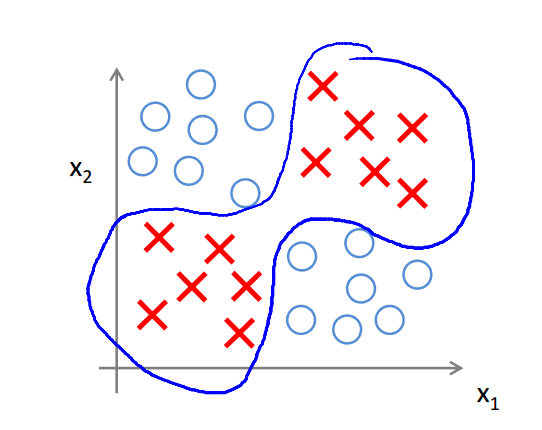
先来看一个分类问题，XOR/XNOR，对于$x_1,x_2 \in {0,1}$，当x1和x2不同（0，1或者1，0）时，y为1，相同时y为0；y=x1 xnor n2

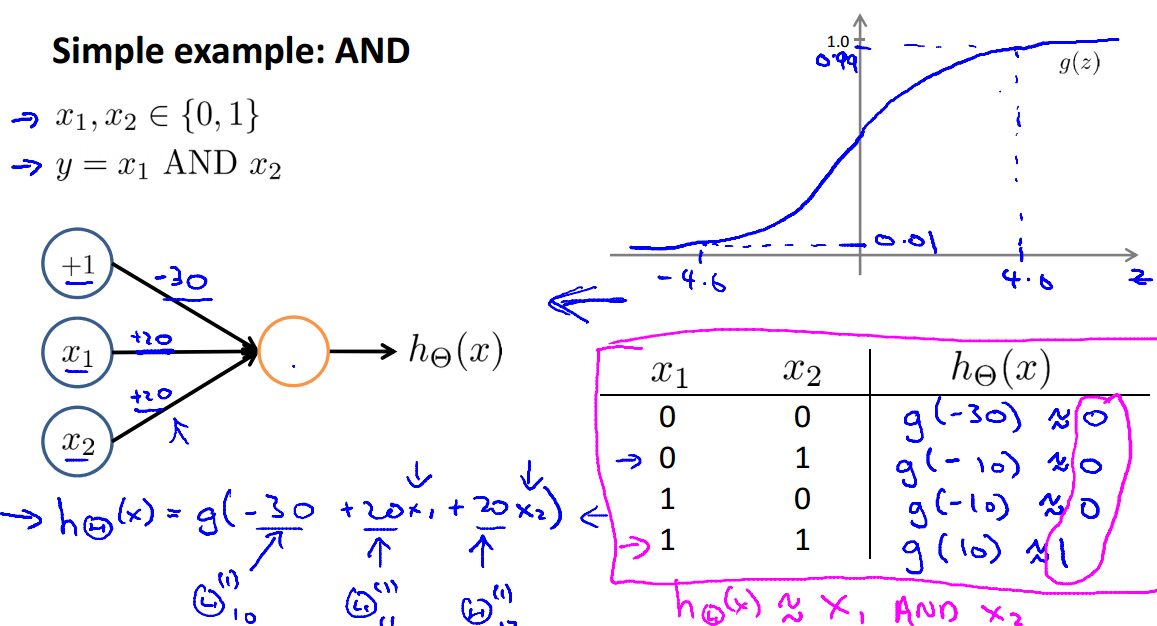
对于一个简单的分类问题 AND：

可以用如下的神经网络结构得到正确的分类结果

同样的，对于OR，我们可以设计出以下的网络，也可以得到正确的结果

5、实例2

接着上面的例子，对于 NOT，以下网络结构可以进行分类：

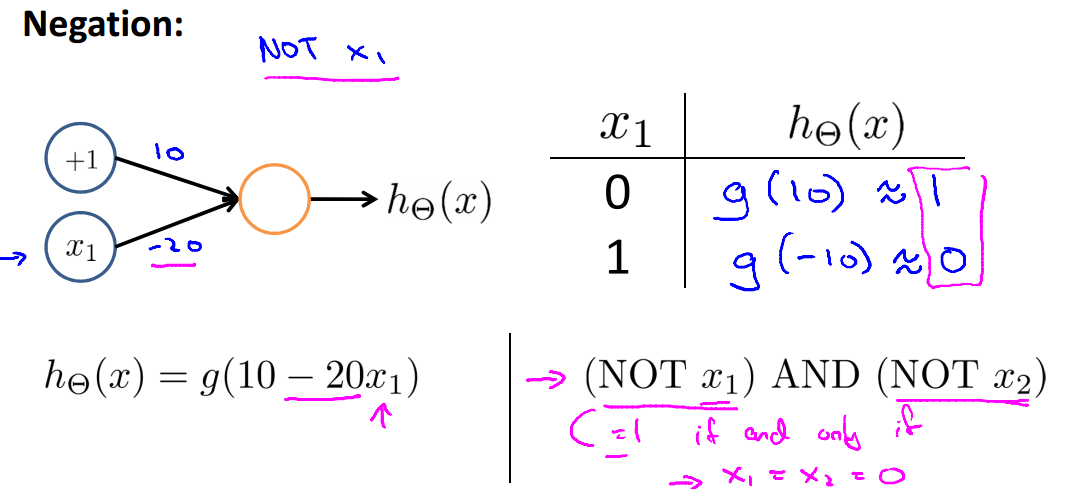
我们回到示例中最初提到的问题：XNOR

当我们组合上述简单例子（AND、OR、NOT）时，就可以得到解决XNOR问题的正确的网络结构：

6、多分类问题

在neural network中的多分类问题的解决，也是用的one vs all的思想，在二分类问题中，我们是输出不是0就是1，而在多分类问题中，输出的结果是一个one hot向量，$h_\Theta(x) \in R^k$，k代表类别数目

比如说对于一个4类问题，输出可能为：

类别1：$\begin{bmatrix}  0 \\ 0 \\ 0 \\ 1 \end{bmatrix}$, 类别2：$\begin{bmatrix}  0 \\ 0 \\ 1 \\ 0 \end{bmatrix}$, 类别3：$\begin{bmatrix}  0 \\ 1 \\ 0 \\ 0 \end{bmatrix}$ , 等等

你不可以把$h_\Theta(x)$输出为1，2，3，4