Naive Bayes (NB Model) 初识

1，Bayes定理 

　　P(A,B)=P(A|B)P(B);

　　P(A,B)=P(B|A)P(A);　　

　　P(A|B)=P(B|A)P(A)/P(B);    贝叶斯定理变形

2,概率图模型

2.1  定义

　　概率图模型是一类用图的形式表示随机变量之间条件依赖关系的概率模型，是概率论与图论的结合。图中的节点表示随机变量，边表示随机变量之间的概率依赖关系.缺少边的节点表示满足条件独立假设。

2.2  随机变量的条件独立性

　　如果有P(A,B|C)=P(A|C)P(B|C),  则称在给定事件C的条件下，两个事件A和B独立，这里假设P(C)>0;

如：设A=2x+z;　　B=y+z;　　C=z;

在C确定的条件下 A,B是独立的。如假设z=0(常数)，则A和B没有任何关联。

　　等价形式P(A|B,C)=P(A|C)　

　推导：　P(A,B|C)=P(A|C)P(B|C);       ...1
　　　　　P(A,B|C)=P(A|B,C)P(B|C);　　  ...2

　　联合1,2式可以=> P(A|C)=P(A|B,C)

2.3 概率图模型的有向图表示

利用有向图来表示变量之间的概率依赖关系,典型应用就是贝叶斯网络.

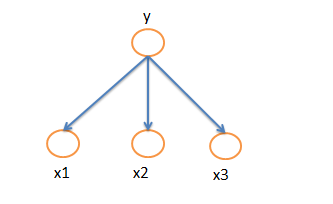
上图NaiveBayes 可以表示为： p(y,x1,x2,x3)=p(y).p(x1|y)p(x2|y)p(x3|y)

3,Naive Bayes Model

3.1 Bayes 决策理论思想

　　朴素贝叶斯是贝叶斯决策理论的一部分， 所以讲述朴素贝叶斯之前有必要快速了解一下贝叶斯决策理论。

　　假设我们有一个数据集，如下图所示：

　

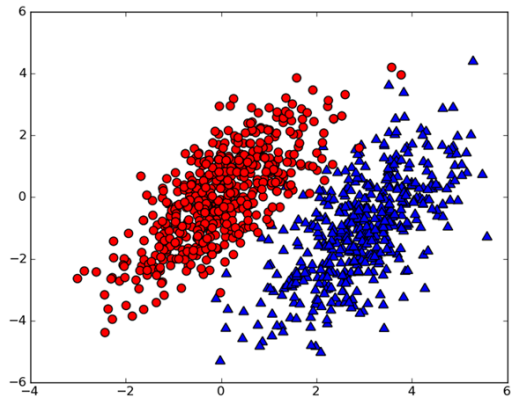
我们用P(c1|x,y) 表示数据点(x,y)属于类别c1的概率(图中红色圆点的概率)，用P(c2|x,y)表示数据点(x,y)属于类别c2的概率(图中绿色的三角形概率)。那么对于一个新的数据点(x,y),我们就可以用一下规则来判断它的类别。

• If p(c1|x, y) > p(c2|x, y), then the class is c1.
• If p(c2|x, y) > p(c1|x, y), then the class is c2.

也就是说，我们会选择高概率对应的类别。这就是贝叶斯决策理论的核心思想， 即选择具有最高概率的决策。

3.2 Naive Bayes 推导

　假设某个体有n项特征（Feature），分别为F₁、F₂、...、F_n。现有m个类别（Category），分别为C₁、C₂、...、C_m。贝叶斯分类器就是计算出概率最大的那　　个　分类，也就是求下面这个算式的最大值：P(C|F1，F2，...，Fn);

　　可以理解为求 在属性F1,F2,....Fn条件下，属于各个类别Ci的概率，然后求出最大的那个P(Ci|F1,F2,...Fn) ，这样就得到F1,F2,...Fn 属于哪一类(Ci)了。

　　使用贝叶斯原理可以写成

　　　

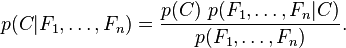
　　因为对于每一个类别的Ci的概率都存在P(F1,F2,......Fn)所以只需要关注P(C)P(F1,F2.....Fn|C)

　　写成联合概率的形式P(C,F1,F2...Fn)=P(C)P(F1,F2.....Fn|C)

　　重复使用贝叶斯原理=>

　　

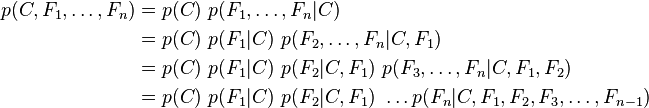
　　现在“朴素”的“条件独立”(2中有推导)假设开始发挥作用:假设每个特征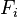对于其他特征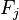,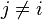是条件独立的。这就意味着

　　　　　　　　　　

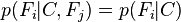
　　对于，所以联合分布模型可以表达为

　　

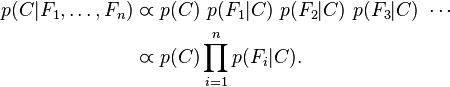
4，例子  ---性别分类

　　下面是一组人类身体特征的统计资料。

身体特征资料统计

性别	身高（英尺）	体重（磅）	脚掌（英寸）
男	6	180	12
男	5.92	190	11
男	5.58	170	12
男	5.92	165	10
女	5	100	6
女	5.5	150	8
女	5.42	130	7
女	5.75	150	9

　　已知某人身高6英尺、体重130磅，脚掌8英寸，请问该人是男是女？

　　即，P(C|F1,F2,F3)的最大概率。

　　根据上面的Naive Bayes Model       P(C|F1,F2,F3)=P(身高|性别) x P(体重|性别) x P(脚掌|性别) x P(性别)

　　这里的困难在于，由于身高、体重、脚掌都是连续变量，不能采用离散变量的方法计算概率。而且由于样本太少，所以也无法分成区间计算。怎么办？

　　这时，可以假设男性和女性的身高、体重、脚掌都是正态分布，通过样本计算出均值和方差，也就是得到正态分布的密度函数。有了密度函数，就可以把值代入，　　算出某一点的密度函数的值。

　　比如，男性的身高是均值5.855、方差0.035的正态分布。所以，男性的身高为6英尺的概率的相对值等于1.5789（大于1并没有关系，因为这里是密度函数的　　　值，只用来反映各个值的相对可能性）。

　　　　

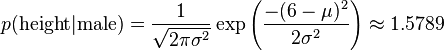
如上，我们就可以推出

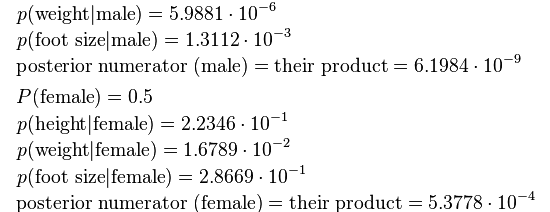
　有了P(height|male),P(weight|male),...我们就可以得到

　　P(height=6|male) x P(weight=130|male) x P(footsize=8|male) x P(male) 
　　　　= 6.1984 x e^-9

　　P(height=6|female) x P(weight=130|female) x P(footsize=8|female) x P(female)
　　　　= 5.3778 x e^-4

可以看到，女性的概率比男性要高出将近10000倍，所以判断该人为女性。

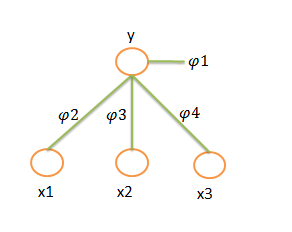
5，概率图模型表示

p(y,x1,x2,x3)=p(y).p(x1|y)p(x2|y)p(x3|y),　　　P(y,x1,x2,x3)=φ1(y)φ(y,x1)φ(y,x2)φ(y,x3)

使用有相图表示：　　　　　　　　　　　　　　　　　　　使用因子图表示：

　　　　　　　　　　　　　　　　　

6，引用

http://en.wikipedia.org/wiki/Naive_Bayes_classifier#Probabilistic_model

http://pan.baidu.com/s/1dD1pcAl